- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Нам векторы идут на помошь
Содержание
- 2. Системы координат на плоскости и в пространствеЧто
- 3. Системы координат на плоскости и в пространствеДекартовы
- 4. Рене ДекартДЕКАРТ (Descartes), Рене31 марта 1596 г.
- 5. Задание прямоугольной системы координат в пространстве:
- 6. Вопросы:1. Сколькими координатами может быть задана точка
- 7. Выполнение задания с последующей проверкой.Начертить прямоугольную трехмерную
- 8. Нахождение координат точек. Точка лежитна осиОу (0;
- 9. Повторение.Даны точки:А (2; -1; 0)В (0; 0;
- 10. Решение задач.Даны координаты четырех вершин кубахуzC1 -
- 11. ВекторыПонятие вектораКоллинеарные векторыРавенство векторовПротивоположные векторыДействия с векторами>>>>Вернуться на главную
- 12. Понятие вектораПусть на тело действует сила в
- 13. Понятие вектораОпределение. Отрезок, для которого указано,
- 14. Понятие вектораНа рисунках вектор изображается отрезком со стрелкойВектор АВ, А – начало вектора, В – конец. CD EF LKАВАВCDEFKL
- 15. Понятие вектораВекторы часто обозначают и одной строчной
- 16. Понятие вектораДлиной или модулем ненулевого вектора АВ
- 17. Коллинеарные векторыНенулевые векторы называются коллинеарными, если они
- 18. Равенство векторовОпределение. Векторы называются равными,
- 19. Противоположные векторы Пусть
- 20. Действия с векторамиОткладывание вектора от данной точкиСумма
- 21. Откладывание вектора от данной точкиЕсли точка А
- 22. Сумма двух векторовРассмотрим пример: Петя из
- 23. Сумма двух векторовПравило треугольника Пусть а
- 24. Законы сложения векторов1) а+b=b+a (переместительный закон) Правило
- 25. Сумма нескольких векторовПравило многоугольникаs=a+b+c+d+e+f k+n+m+r+p=0 abcdefskmnrpO
- 26. Вычитание векторов Определение.
- 27. Умножение вектора на число
- 28. Умножение вектора на число Для любых чисел
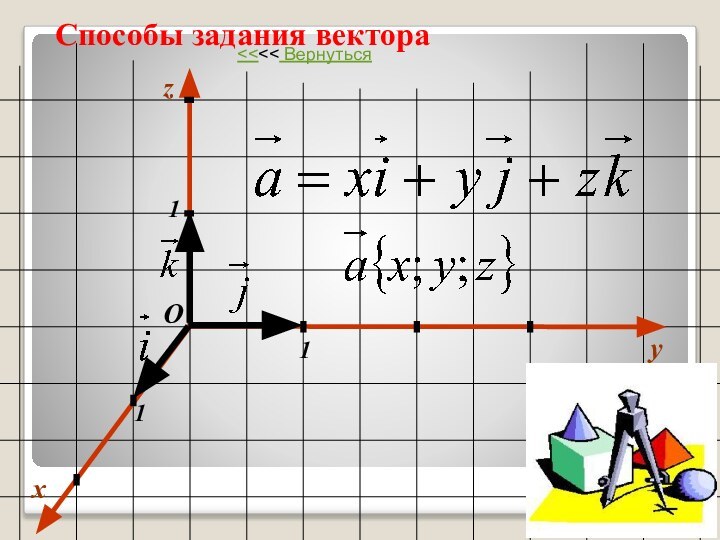
- 29. Способы задания вектораxy111Оz
- 30. Правила действий над векторами с заданными координатами.1.
- 31. Правила действий над векторами с заданными координатами.2.
- 32. Правила действий над векторами с заданными координатами.3.
- 33. Скалярное произведение векторов.Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.
- 34. Решение задачЗадача 1Задача 2Задача 3Задача 4Повторить материалВернуться на главную
- 35. Задача 1 Дано: ABCDA1B1C1D1 - параллелепипед. Упростите выражение: C1D-DA+CD+D1A1+AB1+CC1К списку задач
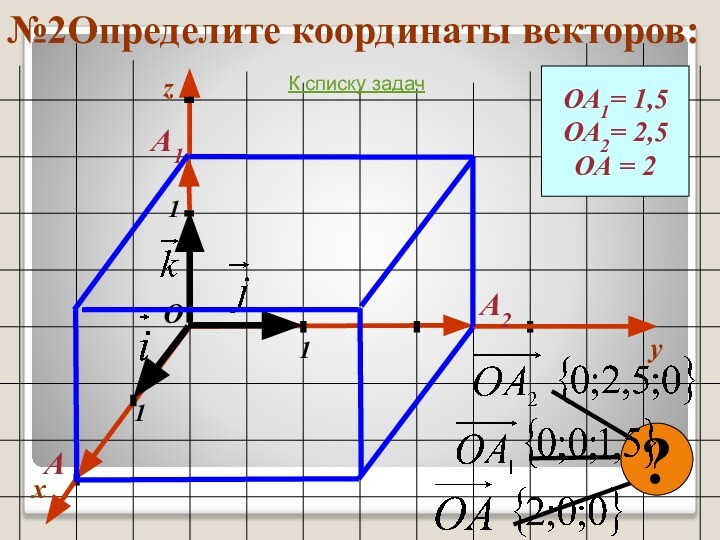
- 36. №2Определите координаты векторов:xy111ОzОА1= 1,5ОА2= 2,5ОА = 2А1А2А?К списку задач
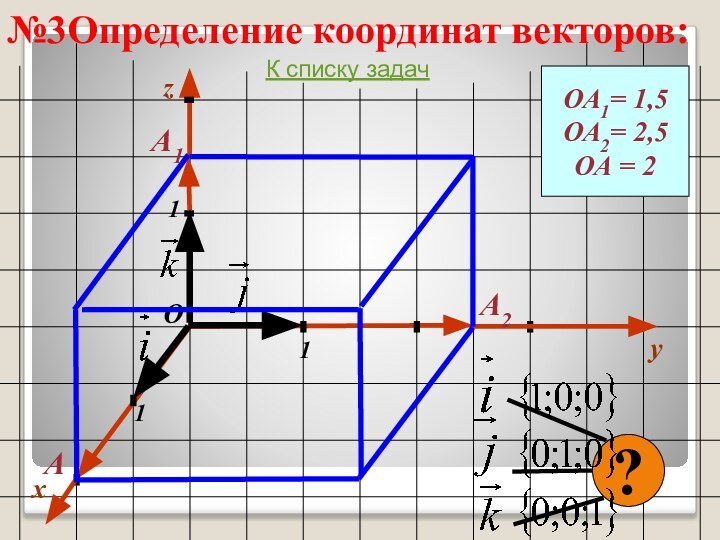
- 37. №3Определение координат векторов:xy111ОzОА1= 1,5ОА2= 2,5ОА = 2А1А2А?К списку задач
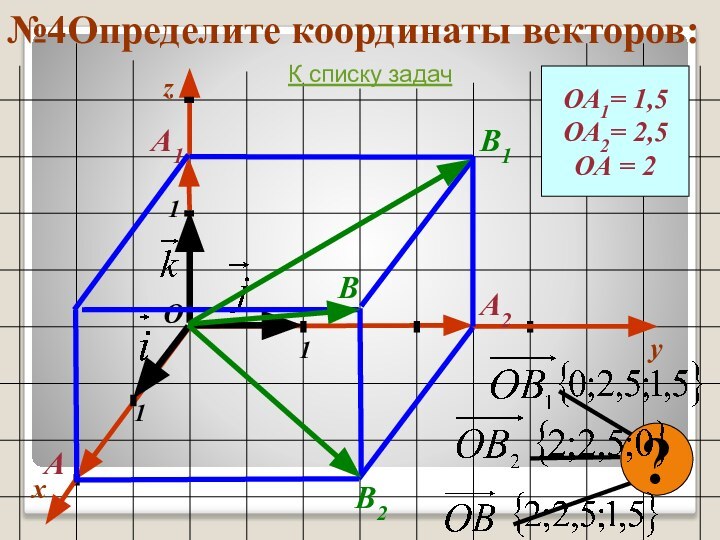
- 38. №4Определите координаты векторов:xy111ОzОА1= 1,5ОА2= 2,5ОА = 2А1А2А?В1В2ВК списку задач
- 39. Скачать презентацию
- 40. Похожие презентации
































Слайд 3
Системы координат на плоскости и в пространстве
Декартовы прямоугольные
координаты О - начало координат, Ох - ось абсцисс, Оy - ось ординат, - базисные векторы, -
абсцисса точки M ( - проекция точки M на ось Ох параллельно оси Оy), - ордината точки M ( - проекция точки M на ось Oy параллельно оси Ox).Расположение точки M на плоскости определяется декартовыми координатами с помощью пары чисел :
— расстояние от точки M до оси y с учетом знака
— расстояние от точки M до оси x с учетом знака
Декартовы координаты в пространстве задаются с помощью точки начала координат и трёх взаимно-перпендикулярных направленных прямых. Прямые занумерованы, задан единичный отрезок. Положение любой точки в пространстве однозначно определено тремя числами: первое число – величина проекции точки на первую ось, второе – величина проекции на вторую ось, третье – на третью.
<< << К разделу<< К разделу Далее<< К разделу Далее >>
Слайд 4
Рене Декарт
ДЕКАРТ (Descartes), Рене
31 марта 1596 г. –
11 февраля 1650 г.
Французский философ, физик, математик и физиолог
Рене Декарт (латинизированное имя – Картезий; Cartesius) родился в Лаэ близ Тура в знатной, но небогатой семье. Образование получил в иезуитской школе Ла Флеш в Анжу (окончил в 1614 г.) и в университете в Пуатье (1616). У Декарта действительное число трактовалось как отношение любого отрезка к единичному, хотя сформулировал такое определение лишь И. Ньютон; отрицательные числа получили у Декарта реальное истолкование в виде направленных ординат. Декарт значительно улучшил систему обозначений, введя общепринятые знаки для переменных величин (x, у, z,...) и коэффициентов (a, b, с,...), а также обозначения степеней (х4, a5,...). Запись формул у Декарта почти ничем не отличается от современной. << << К разделу << К разделу Далее<< К разделу Далее >>
Слайд 5
Задание прямоугольной системы
координат в пространстве:
разделу
>>Оy ┴ Оz
Оz ┴ Оx
Оy ┴ Оx
M (1; 1; 1)
Ох – ось абсцисс
Оу – ось ординат
Оz – ось аппликат
Слайд 6
Вопросы:
1. Сколькими координатами может быть задана точка на
прямой?
Одной.
2. Сколькими координатами может быть задана точка в
координатной плоскости? Двумя.
3. Сколькими координатами может быть задана точка в пространстве?
Тремя.
Слайд 7
Выполнение задания с последующей проверкой.
Начертить прямоугольную трехмерную систему
координат и отметить в ней точки:
А (1; 4;
3); В (0; 5; -3); С (0; 0; 3) и D (4; 0; 4)подсказка
Слайд 8
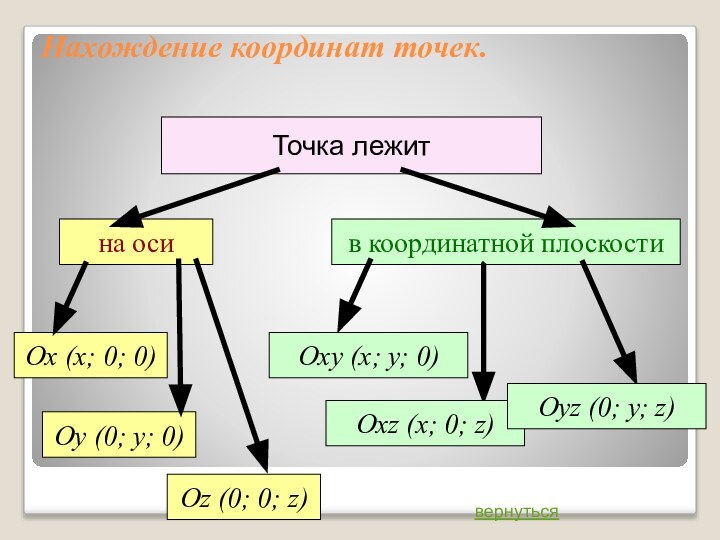
Нахождение координат точек.
Точка лежит
на оси
Оу (0; у; 0)
Ох
(х; 0; 0)
Оz (0; 0; z)
в координатной плоскости
Оху (х;
у; 0)Охz (х; 0; z)
Оуz (0; у; z)
вернуться
Слайд 9
Повторение.
Даны точки:
А (2; -1; 0)
В (0; 0; -7)
С
(2; 0; 0)
D (-4; -1; 0)
Е (0; -3; 0)
F
(1; 2; 3)Р (0; 5; -7)
К (2; 0; -4)
Назовите точки, лежащие
в плоскости Оуz.
Назовите точки, лежащие
в плоскости Охz.
Назовите точки, лежащие
в плоскости Оху.
В (0; 0; -7)
С (2; 0; 0)
Е (0; -3; 0)
Слайд 10
Решение задач.
Даны координаты четырех вершин куба
х
у
z
C1 - ?
C
- ?
A1 (1;0;0)
B1 - ?
D1 - ?
A (0;0;0)
B (0;0;1)
D
(0;1;0)В1 (1; 0; 1)
С (0; 1; 0)
С1 (1; 1; 0)
D1 (1; 1; 1)
Найдите координаты остальных вершин.
На главную
Слайд 11
Векторы
Понятие вектора
Коллинеарные векторы
Равенство векторов
Противоположные векторы
Действия
с векторами
>>>>Вернуться на главную
Слайд 12
Понятие вектора
Пусть на тело действует сила в 8Н.
Стрелка указывает направление силы, а длина отрезка соответствует числовому
значению силы.8Н
<< << К Началу
ДалееДалее>>
Слайд 13
Понятие вектора
Определение.
Отрезок, для которого указано, какой
из его концов считается началом, а какой - концом,
называется направленным отрезком или вектором.Рассмотрим произвольный отрезок. На нем можно указать два направления.
Чтобы выбрать одно из направлений, один конец отрезка назовем НАЧАЛОМ, а другой – КОНЦОМ и будем считать, что отрезок направлен от начала к концу.
<< << К Началу
ДалееДалее>>
Слайд 14
Понятие вектора
На рисунках вектор изображается отрезком со стрелкой
Вектор
АВ, А – начало вектора, В – конец.
CD
EF
LK
А
В
АВ
C
D
E
F
K
L
К НачалуДалееДалее>>
Слайд 15
Понятие вектора
Векторы часто обозначают и одной строчной латинской
буквой со стрелкой над ней:
Любая точка плоскости также является
вектором, который называется НУЛЕВЫМ. Начало нулевого вектора совпадает с его концом: ММ = 0.
a
b
c
М
<< << К Началу
ДалееДалее>>
Слайд 16
Понятие вектора
Длиной или модулем ненулевого вектора АВ называется
длина отрезка АВ:
АВ = а = АВ
= 5с = 17
Длина нулевого вектора считается равной нулю:
ММ = 0.
a
М
В
А
с
<< << К Началу
ДалееДалее>>
Слайд 17
Коллинеарные векторы
Ненулевые векторы называются коллинеарными, если они лежат
либо на одной прямой, либо на параллельных прямых. Коллинеарные
векторы могут быть сонаправленными или противоположно направленными.Нулевой вектор считается коллинеарным любому вектору.
а
b
c
d
m
n
s
L
<< << К Началу
ДалееДалее>>
Слайд 18
Равенство векторов
Определение.
Векторы называются равными, если
они сонаправлены и их длины равны.
а =
b , еслиа b
а = b
а
c
b
d
m
n
s
f
<< << К Началу
ДалееДалее>>
Слайд 19
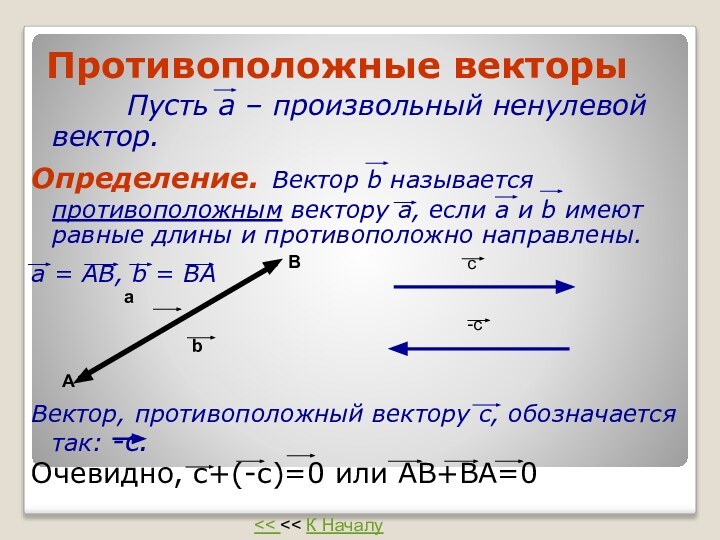
Противоположные векторы
Пусть а
– произвольный ненулевой вектор.
Определение. Вектор b называется противоположным вектору
а, если а и b имеют равные длины и противоположно направлены.a = АВ, b = BA
Вектор, противоположный вектору c, обозначается так: -c.
Очевидно, с+(-с)=0 или АВ+ВА=0
А
B
a
b
c
-c
<< << К Началу
Слайд 20
Действия с векторами
Откладывание вектора от данной точки
Сумма двух
векторов
Законы сложения
Сумма нескольких векторов
Вычитание векторов
Умножение вектора на число
Способы задания
вектораПравила действия над векторами с заданными координатами
Скалярное произведение
>>>>Вернуться на главную страницу
Слайд 21
Откладывание вектора от данной точки
Если точка А –
начало вектора а , то говорят, что вектор а
отложен от точки А.Утверждение: От любой точки М можно отложить вектор, равный данному вектору а, и притом только один.
Равные векторы, отложенные от разных точек, часто обозначают одной и той же буквой
А
а
М
а
<<<< Вернуться
Слайд 22
Сумма двух векторов
Рассмотрим пример:
Петя из дома(D)
зашел к Васе(B), а потом поехал в кинотеатр(К).
В результате этих двух перемещений, которые можно представить векторами DB и BK, Петя переместился из точки D в К, т.е. на вектор DК:DK=DB+BK.
Вектор DK называется суммой векторов DB и BK.
D
B
K
<<<< Вернуться
ДалееДалее>>
Слайд 23
Сумма двух векторов
Правило треугольника
Пусть а и
b – два вектора. Отметим произвольную точку А и
отложим от этой точки АВ = а, затем от точки В отложим вектор ВС = b.АС = а + b
a
b
A
a
b
B
C
<<<<Назад
Вернуться
Слайд 24
Законы сложения векторов
1) а+b=b+a (переместительный закон) Правило параллелограмма
Пусть а и b – два вектора. Отметим
произвольную точку А и отложим от этой точки АВ = а, затем вектор АD = b. На этих векторах построим параллелограмм АВСD.АС = АВ + BС = а+b
АС = АD + DС = b+a
2) (а+b)+c=a+(b+c)
(сочетательный закон)
a
a
b
b
A
D
C
B
a
b
<<<< Вернуться
Слайд 25
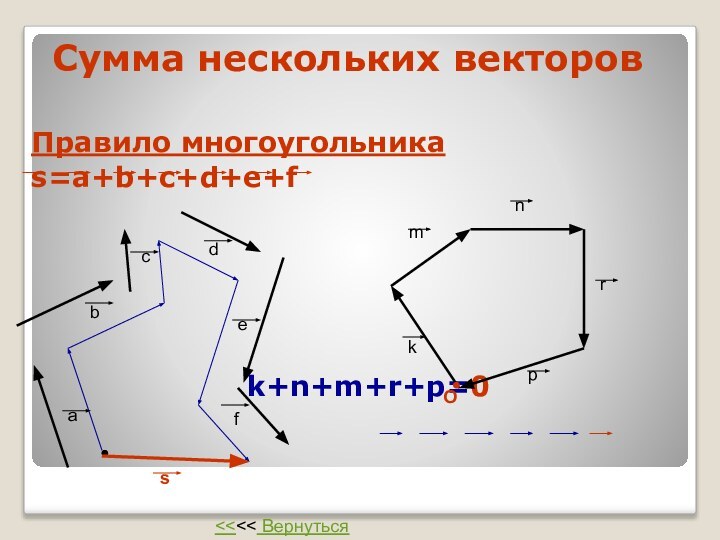
Сумма нескольких векторов
Правило многоугольника
s=a+b+c+d+e+f
k+n+m+r+p=0
a
b
c
d
e
f
s
k
m
n
r
p
O
Вернуться
Слайд 26
Вычитание векторов
Определение. Разностью
двух векторов а и b называется такой вектор, сумма
которого с вектором b равна вектору а.Теорема. Для любых векторов а и b справедливо равенство а - b = а + (-b).
Задача. Даны векторы а и b. Построить вектор а – b.
а
а
b
-b
-b
a - b
<<<< Вернуться
Слайд 27
Умножение
вектора на число
Определение. Произведением ненулевого вектора а на число k называется
такой вектор b, длина которого равна вектору k а , причем векторы а и b сонаправлены при k≥0 ипротивоположно направлены при k<0.
Произведением нулевого вектора на любое число считается нулевой вектор.
Для любого числа k и любого вектора а векторы а и ka коллинеарны.
а
-2a
3а
<<<< Вернуться
ДалееДалее>>
Слайд 28
Умножение
вектора на число
Для любых чисел k, n
и любых векторов а, b справедливы равенства:
(kn) а =
k (na) (сочетательный закон) (k+n) а = kа + na (первый распределительный закон)
K ( а+ b ) = kа + kb (второй распределительный закон)
Свойства действий над векторами позволяют в выражениях, содержащих суммы, разности векторов и произведения векторов на числа, выполнять преобразования по тем же правилам, что и в числовых выражениях. Например,
p = 2( a – b) + ( c + a ) – 3( b – c + a ) =
= 2a – 2b + c + a – 3b + 3c – 3a = - 5b + 4c
<<<< Назад
Вернутся
Слайд 30
Правила действий над векторами с заданными координатами.
1. Равные
векторы имеют равные координаты.
Пусть
, тогда
Следовательно
х1 = х2; у1 =
у2; z1 = z2 <<<< Вернуться
ДалееДалее>>
Слайд 31
Правила действий над векторами с заданными координатами.
2. Каждая
координата суммы двух (и более) векторов равна сумме соответствующих
координат этих векторов.Дано:
Доказать:
Следовательно
<<<< Назад
ДалееДалее>>
Слайд 32
Правила действий над векторами с заданными координатами.
3. Каждая
координата произведения вектора на число равна произведению соответствующей координаты
на это число.Дано:
Доказать:
α – произв.число
4. Каждая координата разности двух векторов равна число равна разности соответствующих координат на этих векторов.
Дано:
Доказать:
<<<< Назад
Вернуться