- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Непараметрический дисперсионный анализ
Содержание
- 2. План лекции:Актуальность темы.Непараметрический дисперсионный анализ для зависимых
- 3. Сравнение более двух зависимых выборок. Критерий Фридмана
- 4. Результаты наблюдения у каждого объекта упорядочиваются (по
- 5. где N-число объектов, k-число уровней фактора (повторных
- 6. Пример:Результаты тестирования студентов по семестрамH0- результаты тестирования по семестрам статистически значимо не различаются
- 7. Ранжируем по строкам
- 8. Вычислим сумму рангов для каждого семестра RiВычислим эмпирическое значение критерия χ2 -Фридмана
- 9. Найдем χ2 крит для df=3 и α=0,05.
- 10. Сравнение более двух независимых выборок. Критерий Краскэла-Уоллиса.Критерий
- 11. Значения выборок объединяются в один упорядоченный ряд.Значения
- 12. Чем сильнее различаются выборки, тем больше критерий
- 13. Пример:
- 15. Проверяем правильность расчетов.Общая сумма рангов должна равняться:
- 16. Критерий Колмогорова-Смирнова используется для сравнения эмпирического распределения
- 17. В качестве меры расхождения между теоретической F(x)
- 18. Процедура расчетов1. Данные в выборке ранжируются по
- 19. Пример 1. Равномерное распределение.У студентов в возрасте
- 20. Упорядочим эмпирические частоты по возрастанию:8 8 9
- 21. Эмпирическое значение критерия равно:Критическое значение критерия находим
- 22. Для применения критерия необходимо выполнение следующих условий:Измерения
- 23. Пример 2: Нормальное распределениеСреднее арифметическое = -0,308;
- 24. Функции распределения
- 25. Процедура расчетов1. Данные в выборке ранжируются по
- 26. D=4,96/20 =0,248 < Dкрит = 0,304 (α=0,05); нулевая гипотеза не отклоняется. Данные подчиняются нормальному закону распределения.
- 27. ЗаключениеТаким образом, нами рассмотрены основы непараметрического дисперсионного анализа, применение критерия Колмогорова-Смирнова
- 28. РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА:Основная литература:Попов А.М. Теория вероятней и
- 29. Скачать презентацию
- 30. Похожие презентации
План лекции:Актуальность темы.Непараметрический дисперсионный анализ для зависимых выборок. Непараметрический дисперсионный анализ для независимых выборок. Критерий Колмогорова-Смирнова. Заключение.




















Слайд 3
Сравнение более двух зависимых выборок.
Критерий Фридмана (χ2) -
это непараметрический аналог дисперсионного анализа повторных измерений (ANOVA).
Проверяется гипотеза
о различии более двух зависимых выборок по уровню выраженности изучаемого признака.
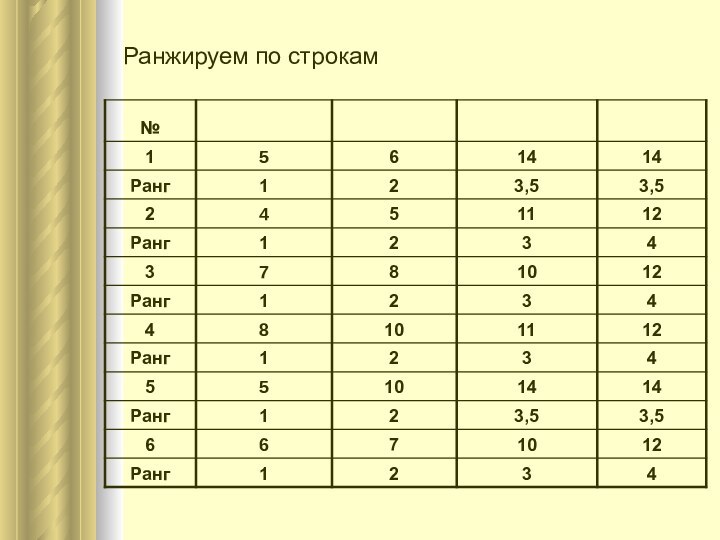
Слайд 4 Результаты наблюдения у каждого объекта упорядочиваются (по строке).
Причем отдельно упорядочиваем значения у каждого объекта независимо от
всех остальных. Таким образом получается столько упорядоченных рядов, сколько объектов участвует в исследовании.Вычисляется сумма рангов для каждого уровня фактора (по столбцам).
Вычисляется эмпирическое значение критерия χ2 -Фридмана
Чем больше различаются зависимые выборки по изучаемому признаку, тем больше эмпирическое значение критерия χ2 –Фридмана.
Слайд 5 где N-число объектов, k-число уровней фактора (повторных измерений),
Ri-сумма рангов для соответствующего уровня i.
Находится χ2крит для df=k-1
и α=0,05.При k=3, N>9 или k>3, N>4 пользуются обычной таблицей распределения χ2 .
При k=3, N<10 или k=4, N<5 пользуются дополнительной таблицей критических значений χ2- Фридмана.
Определяется уровень значимости.
Если χ2 эмп ≥ χ2 крит нулевая гипотеза отвергается. Различия статистически значимы.
Если χ2 эмп < χ2 крит нулевая гипотеза не отвергается. Различия статистически не значимы.
Если разброс сумм велик и различия статистически значимы, переходим к межгрупповым сравнениям по критерию Вилкоксона с поправкой Бонферрони.
Слайд 6
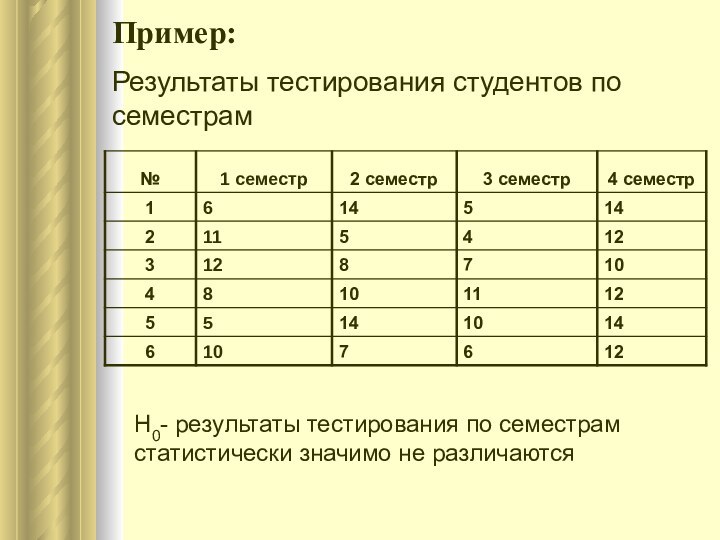
Пример:
Результаты тестирования студентов по семестрам
H0- результаты тестирования по
семестрам статистически значимо не различаются
Слайд 8
Вычислим сумму рангов для каждого семестра Ri
Вычислим эмпирическое
значение критерия χ2 -Фридмана
Слайд 9 Найдем χ2 крит для df=3 и α=0,05. χ2
крит=7,815
Так как 8,6 > 7,815 нулевая гипотеза отвергается.
Различия
результатов тестирования по семестрам статистически значимы на уровне α<0,05.По каким семестрам результаты различаются, проверяем по критерию Вилкоксона с поправкой Бонферрони:
Т12 Т13 Т14 Т23 Т24 Т34
Слайд 10
Сравнение более двух независимых выборок. Критерий Краскэла-Уоллиса.
Критерий Краскэла-Уоллиса
(Н) - это непараметрический аналог однофакторного дисперсионного анализа для независимых выборок.
Так же как критерий Манна-Уитни U показывает насколько совпадают (пересекаются) несколько рядов значений измеренного признака. Чем меньше совпадений, тем больше различаются ряды, соответствующие сравниваемым выборкам.
Слайд 11
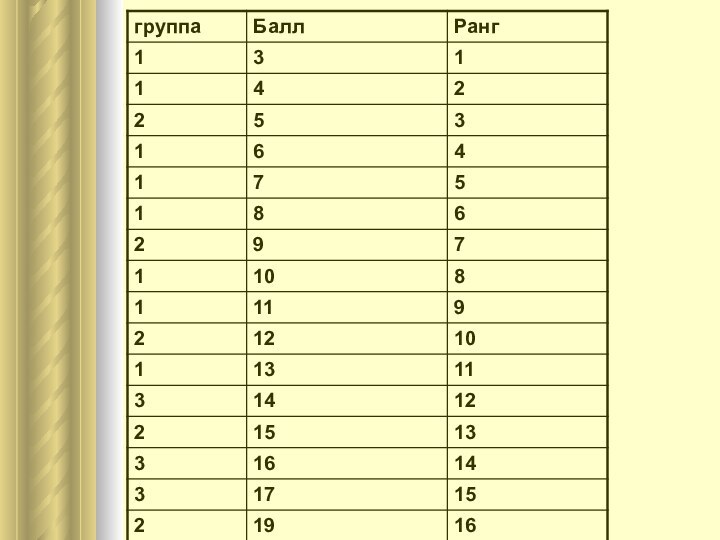
Значения выборок объединяются в один упорядоченный ряд.
Значения объединенного
ряда ранжируются.
Записываются ранги отдельно для каждой выборки.
Вычисляются суммы рангов
для каждой выборки.Вычисляется эмпирическое значение критерия Нэмп по формуле:
N-суммарная численность всех выборок, k-количество сравниваемых выборок, Ri-сумма рангов для выборки i, ni-численность выборки i.
Слайд 12 Чем сильнее различаются выборки, тем больше критерий Н
и тем меньше уровень значимости.
Находится критическое значение критерия Нкрит
(α=0,05, df=k-1)Если сравниваются 3 выборки и объем каждой выборки меньше 5, пользуются таблицами критических значений Н-Краскэла-Уоллиса.
Если объем каждой выборки больше 5 и число выборок больше трех, пользуются таблицами распределения χ2 .
Определяем уровень значимости.
Если χ2 эмп ≥ χ2 крит нулевая гипотеза отвергается. Различия статистически значимы.
Если χ2 эмп < χ2 крит нулевая гипотеза не отвергается. Различия статистически не значимы.
Слайд 15
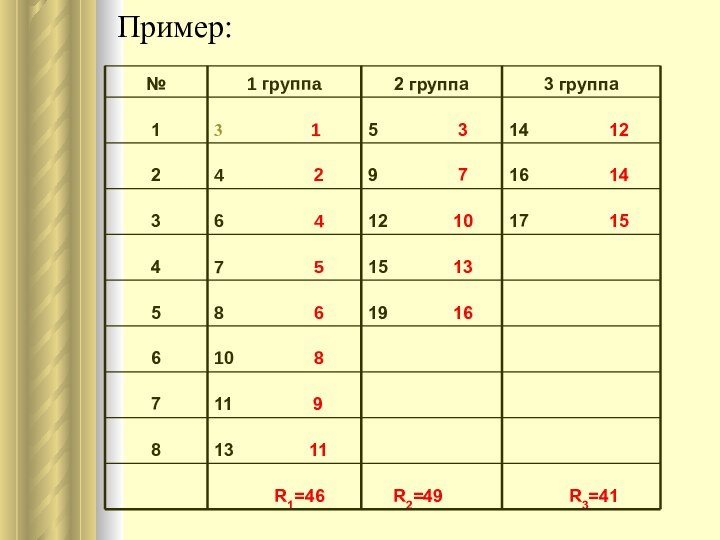
Проверяем правильность расчетов.
Общая сумма рангов должна равняться: N(N+1)/2=16⋅17/2=136
R1+R2+R3=46+49+41=136
Вычисляем
Н:
По таблице критических значений находим χ2 для α=0,05 и
df=3-1=2 χ2 крит=5,992Так как 6,575 > 5,992 нулевая гипотеза отвергается. Различия в группах статистически значимы.
По каким группам результаты различаются, проверяем по критерию Манна-Уитни с поправкой Бонферрони:
U12 U13 U23
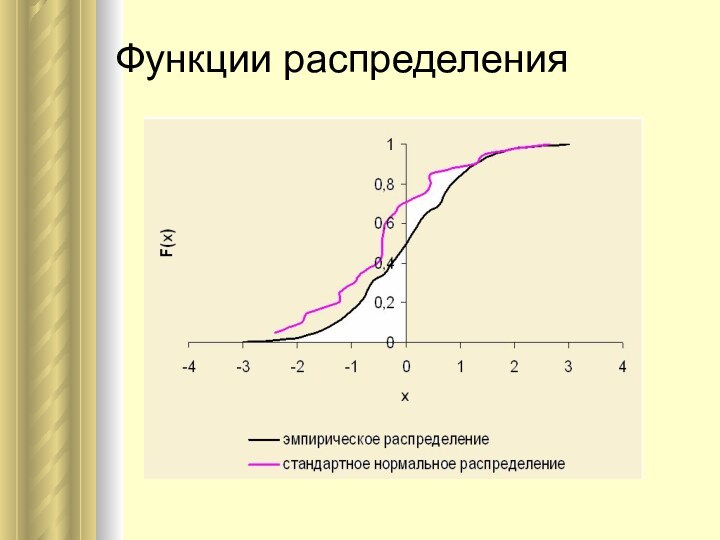
Слайд 16 Критерий Колмогорова-Смирнова используется для сравнения эмпирического распределения с
теоретическим или двух эмпирических распределений друг с другом.
При применении
этого критерия сравниваются теоретическая F(x) и эмпирическая Fn(x) функции распределения случайной величины (накопленные частоты). Если разность накопленных частот в двух распределениях оказывается большой, то различия между двумя распределениями являются существенными.
Критерий Колмогорова-Смирнова
Слайд 17 В качестве меры расхождения между теоретической F(x) и
эмпирической Fn(x) функциями распределения непрерывной случайной величины Х используется
модуль максимальной разностиDn = max|F(x) - Fn(x)|.
Слайд 18
Процедура расчетов
1. Данные в выборке ранжируются по возрастанию.
2.
Вычисляются кумулятивные разности:
3. Находится абсолютное наибольшее значение кумулятивных
разностей4. Вычисляется значение D критерия Колмогорова-Смирнова и сравнивается с соответствующим табличным значением.
Слайд 19
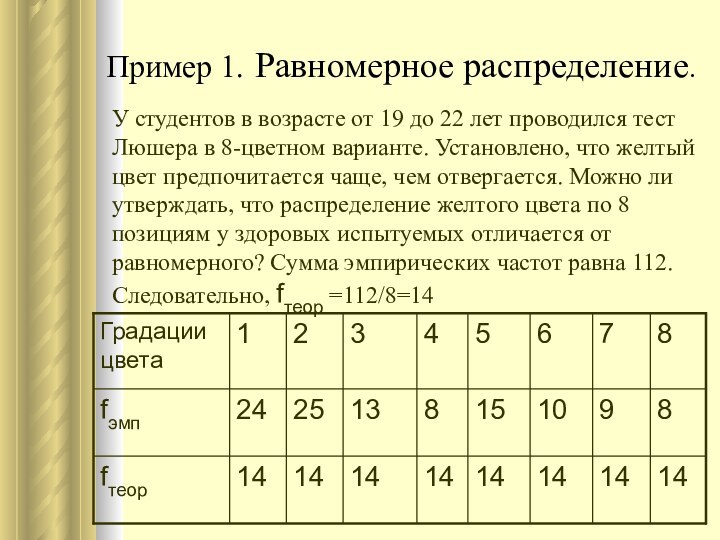
Пример 1. Равномерное распределение.
У студентов в возрасте от
19 до 22 лет проводился тест Люшера в 8-цветном
варианте. Установлено, что желтый цвет предпочитается чаще, чем отвергается. Можно ли утверждать, что распределение желтого цвета по 8 позициям у здоровых испытуемых отличается от равномерного? Сумма эмпирических частот равна 112. Следовательно, fтеор =112/8=14
Слайд 20
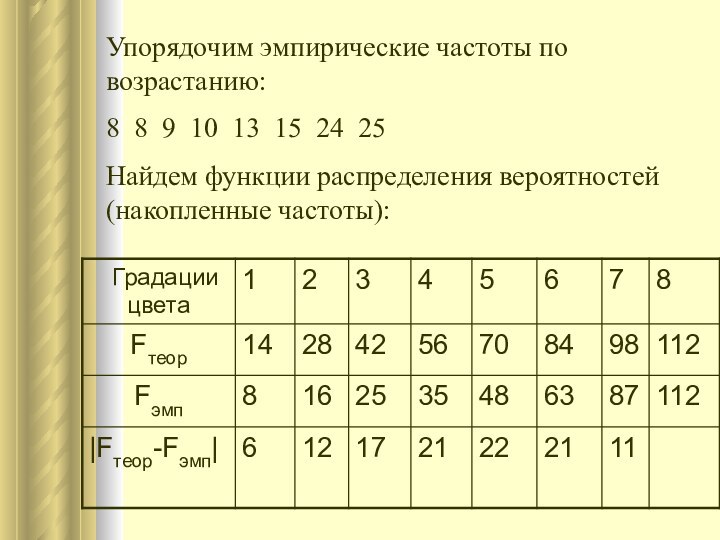
Упорядочим эмпирические частоты по возрастанию:
8 8 9 10
13 15 24 25
Найдем функции распределения вероятностей (накопленные
частоты):
Слайд 21
Эмпирическое значение критерия равно:
Критическое значение критерия находим по
таблице.
Если число элементов выборки больше 100, критические значения
критерия Колмогорова-Смирнова вычисляются по формулам:для α=0,05 Dкр=1,36/√n
для α=0,01 Dкр=1,63/√n
Так как Dкр=1,36/√112=0,128; Dкр=1,63/√112=0,154
Dэмп> Dкр 0,196>0,154. Нулевая гипотеза отвергается, распределение желтого цвета по 8 позициям отличается от равномерного.
Слайд 22
Для применения критерия необходимо выполнение следующих условий:
Измерения должны
быть проведены в шкале интервалов и отношений
Выборки должны быть
случайными и независимымиЭмпирические данные должны допускать упорядочение по возрастанию или убыванию
Суммарный объем двух выборок ≥ 50. С увеличением объема выборки точность критерия повышается.
Слайд 23
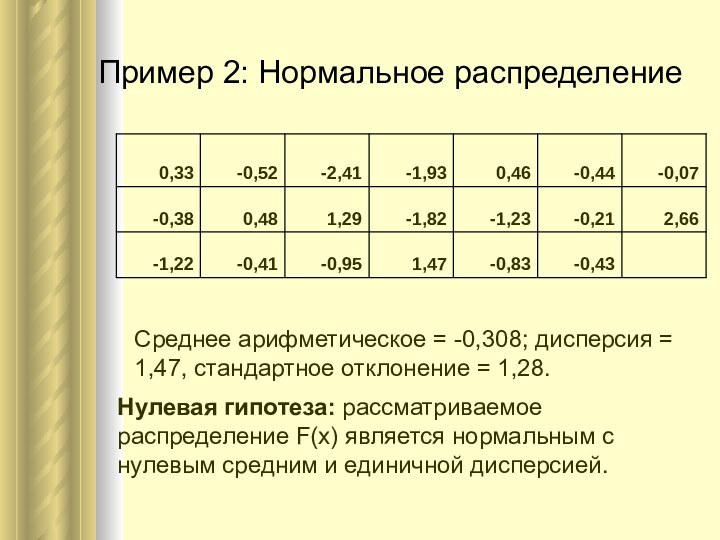
Пример 2: Нормальное распределение
Среднее арифметическое = -0,308; дисперсия
= 1,47, стандартное отклонение = 1,28.
Нулевая гипотеза: рассматриваемое распределение
F(x) является нормальным с нулевым средним и единичной дисперсией.
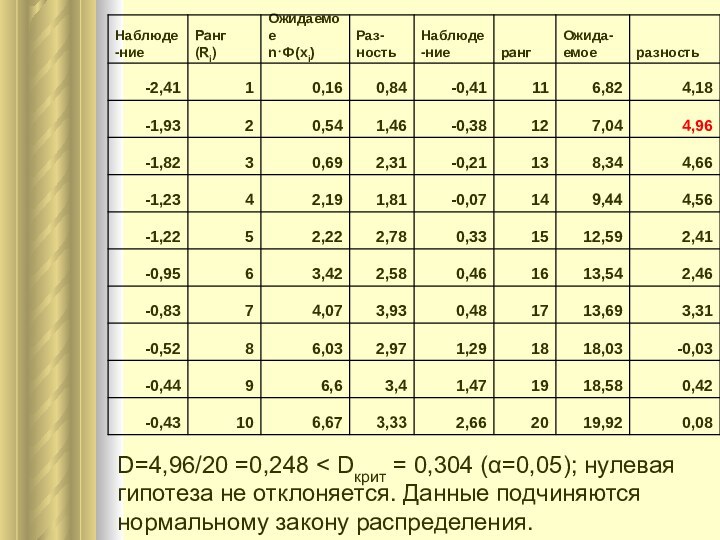
Слайд 25
Процедура расчетов
1. Данные в выборке ранжируются по возрастанию.
2.
Вычисляются кумулятивные разности:
3. Находится абсолютное наибольшее значение кумулятивных
разностей4. Вычисляется значение D критерия Колмогорова-Смирнова и сравнивается с соответствующим табличным значением.
Слайд 26 D=4,96/20 =0,248 < Dкрит = 0,304 (α=0,05); нулевая
гипотеза не отклоняется. Данные подчиняются нормальному закону распределения.
Слайд 27
Заключение
Таким образом, нами рассмотрены основы непараметрического дисперсионного анализа,
применение критерия Колмогорова-Смирнова
Слайд 28
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА:
Основная литература:
Попов А.М. Теория вероятней и математическая
статистика /А.М. Попов, В.Н. Сотников. – М.: ЮРАЙТ, 2011.
– 440 с.Герасимов А. Н. Медицинская статистика: учебное пособие / А. Н. Герасимов. – М. : Мед. информ. агентство, 2007. – 480 с.
Балдин К. В. Основы теории вероятностей и математической статистики : учебник / К. В. Балдин. – М. : Флинта, 2010. – 488с.





























