Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть

Презентация на тему Неравенства и их системы

Содержание

2. 1)Определение 2) Виды 3) Свойства числовых
3. Запись вида а>в или а
4. Неравенства вида а≥в, а≤в называются ……Неравенства вида а>в, а
5. 1) Если а>в, то вв, в>с, то
6. 1). Любой член неравенства можно переносить из
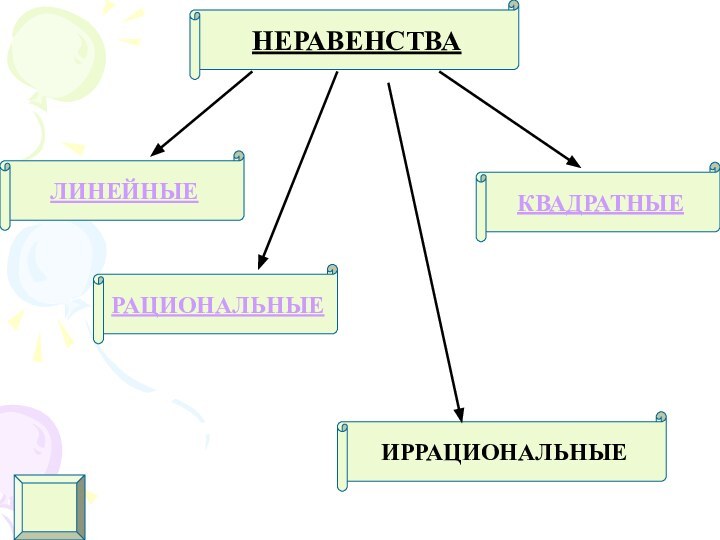
7. ЛИНЕЙНЫЕКВАДРАТНЫЕРАЦИОНАЛЬНЫЕИРРАЦИОНАЛЬНЫЕНЕРАВЕНСТВА
8. I)I)Линейное неравенство 2х+4≥6; 2х≥-2;
9. Решить неравенства1) х+2≥2,5х-1;2)х- 0,25(х+4)+0,5(3х-1)>3;3)4)х²+х
10. Найдите наименьшие целые числа, являющиеся решениями неравенств1)2(х-3)-1-3(х-2)-4(х+1)>0;2)0,2(2х+2)-0,5(х-1)
11. II)II)Квадратные неравенстваСпособы решения:Графический С С применением систем неравенствМетод интервалов
12. 1.1)Метод интервалов(для решения квадратного уравнения)
13. x²+x-6=0; (х-2)(х+3)=0; Ответ: (-∞;-3)v(2;+∞)
14. Решение неравенства методом интервалов1) х(х+7)≥0;2)(х-1)(х+2)≤0;3)х-х²+20;5)х(х+2)
15. Домашняя работа:Сборник 1).стр. 109 № 128-131Сборник 2).стр.111 №3.8-3.10; 3.22;3.37-3.4
16. 1.21.2)1.2)Решение квадратных неравенств графически1). Определить направление ветвей
17. Пример:х²+5х-6≤0y= х²+5х-6 (квадратичная функция, график парабола, а=1,
18. Решите графически неравенства:1)х²-3х0;3)х²+2х≥0;4) -2х²+х+1≤0(0;3)(-∞;0)U(4;+∞) (-∞;-2]U[0;+∞) (-∞;-0,5]U[1;+∞)
19. Домашнее задание:Сборник 1)стр. 115 №176-179.
20. 1.21.2)1.2)Решение квадратных неравенств с помощью систем
21. Сборник 1)стр. 109 №132Сборник 2) Стр. 112-113
22. III).III).Рациональные неравенстваIII).Рациональные неравенства III).Рациональные неравенства вида
23. Системы неравенств.
24. 1) Содержащие линейные неравенства.2) Содержащие квадратное(рациональное) неравенство
25. 1) 5х+1>6 5x>5 x>1 2x-4
26. 2) х²-1>0 (x-1)(x+1)>0 x+4
27. 3) х²-4>0 x²-3x+5
28. 4)-12
30. Скачать презентацию
31. Похожие презентации

1)Определение 2) Виды 3) Свойства числовых неравенств 4) Основные свойства неравенств 4) Типы 5) Способы решения

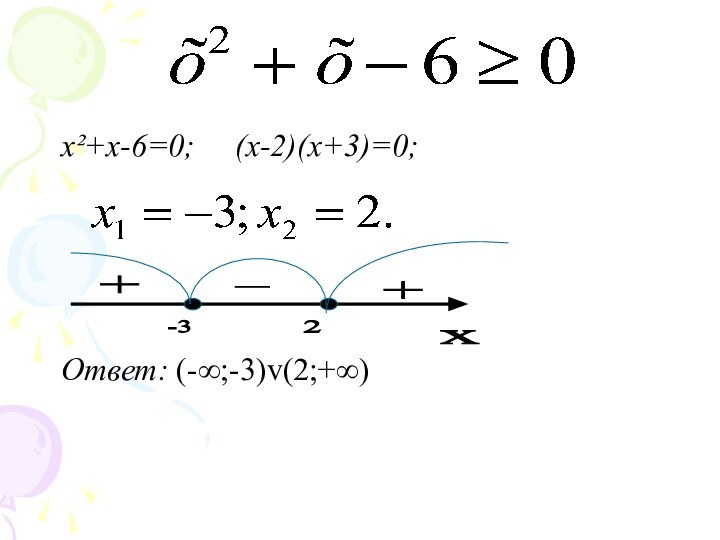
НеравенстваНеравенства и их системы.Учитель Бузецкая Т.В.Государственное бюджетное общеобразовательное учреждение средняя школа 523 Санкт-Петербурга

Неравенства вида а≥в, а≤в называются ……Неравенства вида а>в, а

1) Если а>в, то вв, в>с, то а>с.3) Если а>в, с-любое число,

1). Любой член неравенства можно переносить из одной части неравенства в другую,

ЛИНЕЙНЫЕКВАДРАТНЫЕРАЦИОНАЛЬНЫЕИРРАЦИОНАЛЬНЫЕНЕРАВЕНСТВА

I)I)Линейное неравенство 2х+4≥6; 2х≥-2; х≥-1;

Решить неравенства1) х+2≥2,5х-1;2)х- 0,25(х+4)+0,5(3х-1)>3;3)4)х²+х

Найдите наименьшие целые числа, являющиеся решениями неравенств1)2(х-3)-1-3(х-2)-4(х+1)>0;2)0,2(2х+2)-0,5(х-1)

II)II)Квадратные неравенстваСпособы решения:Графический С С применением систем неравенствМетод интервалов

1.1)Метод интервалов(для решения квадратного уравнения) ах²+вх+с>01)

x²+x-6=0; (х-2)(х+3)=0; Ответ: (-∞;-3)v(2;+∞) х +

Решение неравенства методом интервалов1) х(х+7)≥0;2)(х-1)(х+2)≤0;3)х-х²+20;5)х(х+2)

Домашняя работа:Сборник 1).стр. 109 № 128-131Сборник 2).стр.111 №3.8-3.10; 3.22;3.37-3.4

1.21.2)1.2)Решение квадратных неравенств графически1). Определить направление ветвей параболы, по знаку первого коэффициента

Пример:х²+5х-6≤0y= х²+5х-6 (квадратичная функция, график парабола, а=1, ветви направлены вверх)х²+5х-6=0; корни уравнения:

Решите графически неравенства:1)х²-3х0;3)х²+2х≥0;4) -2х²+х+1≤0(0;3)(-∞;0)U(4;+∞) (-∞;-2]U[0;+∞) (-∞;-0,5]U[1;+∞)

Домашнее задание:Сборник 1)стр. 115 №176-179.

1.21.2)1.2)Решение квадратных неравенств с помощью систем

Сборник 1)стр. 109 №132Сборник 2) Стр. 112-113 № 3.20, 3.21,

III).III).Рациональные неравенстваIII).Рациональные неравенства III).Рациональные неравенства вида решают методом интервалов.1) Раскладывают на линейные

1) Содержащие линейные неравенства.2) Содержащие квадратное(рациональное) неравенство и линейное неравенство.3) Содержащие квадратные

Литература1)Кузнецова Л.В.«Сборник заданий для проведения письменного экзамена по алгебре» «Дрофа», 2007 год2)

Слайды презентации

Слайд 2
1)Определение
2) Виды
3) Свойства

1)Определение 2) Виды 3) Свойства числовых неравенств 4) Основные свойства

числовых неравенств
4) Основные свойства неравенств
4) Типы
5)

Способы решения

Слайд 3

Запись вида
а>в или а

Слайд 4

Неравенства вида а≥в, а≤в называются ……

Неравенства вида а>в,

а

Слайд 5
1) Если а>в, то вв, в>с, то

1) Если а>в, то вв, в>с, то а>с.3) Если а>в, с-любое

а>с.
3) Если а>в, с-любое число, то а+с>в+с.
4) Если а>в,

с>х, то а+с>в+х.
5) Если а>в, с>0, то ас>вс.
6) Если а>в, с<0, то ас<вс.
7) Если а>о, с>0, а>с, то >

Слайд 6
1). Любой член неравенства можно переносить из одной

1). Любой член неравенства можно переносить из одной части неравенства в

части неравенства в другую, изменив его знак на противоположный,

при этом знак неравенства не меняется.
2).Обе части неравенства можно умножить или разделить на одно и тоже положительное число, при этом знак неравенства не изменится. Если это число отрицательное, то знак неравенства изменится на противоположное

Слайд 7

ЛИНЕЙНЫЕ
КВАДРАТНЫЕ
РАЦИОНАЛЬНЫЕ
ИРРАЦИОНАЛЬНЫЕ
НЕРАВЕНСТВА

Слайд 8
I)I)Линейное неравенство
2х+4≥6;
2х≥-2;
х≥-1;

-1 х Ответ: [-1;+∞).

Слайд 9 Решить неравенства
1) х+2≥2,5х-1;
2)х- 0,25(х+4)+0,5(3х-1)>3;
3)

4)х²+х

Слайд 10 Найдите наименьшие целые числа, являющиеся решениями неравенств
1)2(х-3)-1-3(х-2)-4(х+1)>0;
2)0,2(2х+2)-0,5(х-1)

натуральные числа, являющиеся решениями неравенства
3х-3

Слайд 11
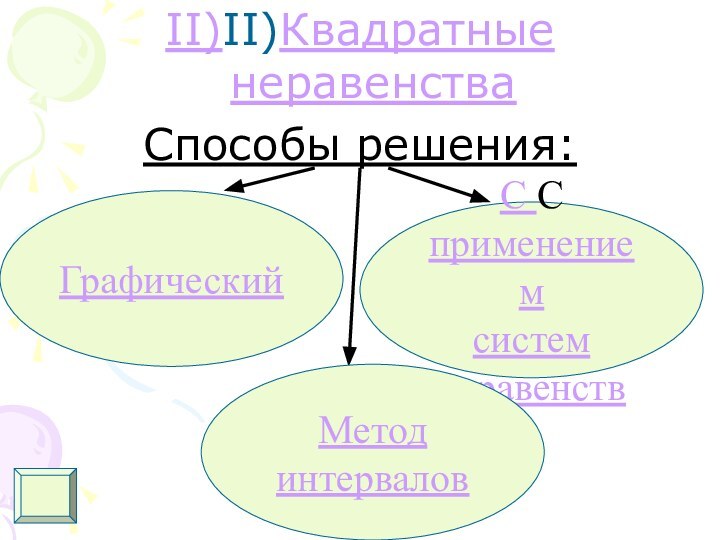
II)II)Квадратные неравенства
Способы решения:
Графический
С С применением
систем
неравенств
Метод

интервалов

Слайд 12 1.1)Метод интервалов
(для решения квадратного уравнения)

ах²+вх+с>0
1) Разложим данный многочлен на множители,

т.е. представим в виде
а(х- )(х- )>0.
2)корни многочлена нанести на числовую ось;
3)Определить знаки функции в каждом из промежутков;
4)Выбрать подходящие интервалы и записать ответ

Слайд 13 x²+x-6=0; (х-2)(х+3)=0;

Ответ: (-∞;-3)v(2;+∞)

х
+
2

-3
+
-

Слайд 14 Решение неравенства методом интервалов
1) х(х+7)≥0;
2)(х-1)(х+2)≤0;
3)х-х²+20;
5)х(х+2)

Слайд 15
Домашняя работа:
Сборник 1).стр. 109 № 128-131
Сборник 2).стр.111 №3.8-3.10;

3.22;3.37-3.4

Слайд 16 1.21.2)1.2)Решение квадратных неравенств графически
1). Определить направление ветвей параболы,

1.21.2)1.2)Решение квадратных неравенств графически1). Определить направление ветвей параболы, по знаку первого

по знаку первого коэффициента квадратичной функции.
2).Найти корни соответствующего квадратного

уравнения;
3).Построить эскиз графика и по нему определить промежутки, на которых квадратичная функция принимает положительные или отрицательные значения

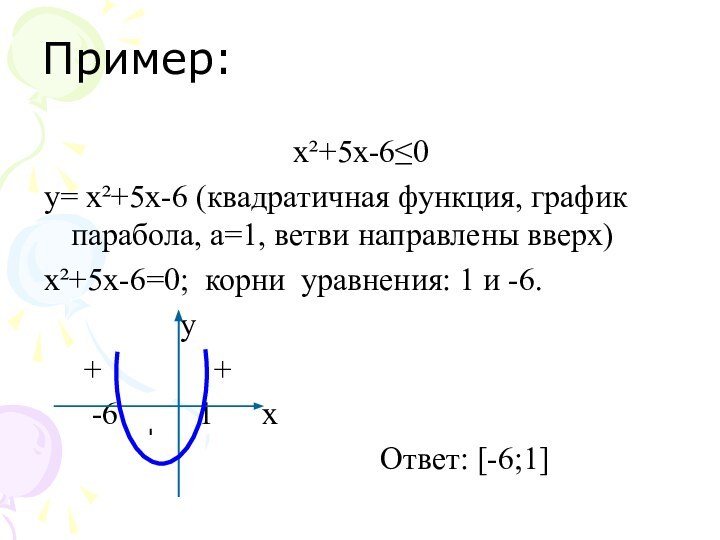
Слайд 17 Пример:
х²+5х-6≤0
y= х²+5х-6 (квадратичная функция, график парабола, а=1, ветви

Пример:х²+5х-6≤0y= х²+5х-6 (квадратичная функция, график парабола, а=1, ветви направлены вверх)х²+5х-6=0; корни

направлены вверх)
х²+5х-6=0; корни уравнения: 1 и -6.

у
+ +
-6 1 x
Ответ: [-6;1]

Слайд 18 Решите графически неравенства:
1)х²-3х0;
3)х²+2х≥0;
4) -2х²+х+1≤0

(0;3)

(-∞;0)U(4;+∞)

(-∞;-2]U[0;+∞)
(-∞;-0,5]U[1;+∞)

Слайд 19
Домашнее задание:
Сборник 1)стр. 115 №176-179.

работы №47,45,42,17,12

(задание №5)
Сборник 2)стр. 116 № 4.4,4.5, 4.11.
работы №6, задание 13

Слайд 20 1.21.2)1.2)Решение квадратных неравенств с помощью систем

Слайд 21
Сборник 1)стр. 109 №132
Сборник 2) Стр. 112-113 №

3.20, 3.21,

3.39-3.42

Слайд 22 III).III).Рациональные неравенстваIII).Рациональные неравенства III).Рациональные неравенства вида решают методом

интервалов.
1) Раскладывают на линейные множители числитель P(x) и знаменатель Q(x).

Если это удается, то дальше поступают так.
2) На числовую ось наносят корни всех линейных множителей. На каждом из промежутков, на которые эти точки разбивают ось, дробь сохраняет знак
3) Определяют знак дроби на каждом промежутке.
4) Записывают ответ

Слайд 23

Системы неравенств.

Слайд 24
1) Содержащие линейные неравенства.
2) Содержащие квадратное(рациональное) неравенство и

1) Содержащие линейные неравенства.2) Содержащие квадратное(рациональное) неравенство и линейное неравенство.3) Содержащие

линейное неравенство.
3) Содержащие квадратные неравенства.
4)Двойное неравенство, которое решается с

помощью систем.
5) Неравенства с модулем

Слайд 25
1) 5х+1>6 5x>5

x>1
2x-4

2x<7 ; x<3,5.

1 3,5 x
Ответ: (1;3,5).
Задания:
Сборник 1). Стр. 111№139-142
стр. 170-172 № 711-766
Сборник 2).стр. 110 № 3.4-3.7

Слайд 26 2) х²-1>0 (x-1)(x+1)>0

x+4

+ - +
-4 -1 1 x
Ответ: (-∞;-4).
Задания:
Сборник 1).стр. 111 № 143-145
Сборник 2). Стр. 112-113 №3.24, 3.25

Слайд 27 3) х²-4>0
x²-3x+5

каждое квадратное неравенство в отдельности. Изображаем решения на числовой

прямой и смотрим пересечения этих решений. Записываем ответ.
Задания:
Сборник 1). Стр. 111 № 146-147
Сборник 2).стр. 113, 115 № 3.27, 3.29,
3.47, 3.48

Слайд 28
4)-12

x

x-1>-12; x>-11.
Ответ: (-11;2).
Задания:
Сборник 1)стр. 109 № 126-127, 134,
стр. 172 №783-790
Сборник 2)Стр. 111 №3.9

Слайд 29
5)| 3х-2|

3x-2>-10 x>

3x-2<10; x<4.

- Предыдущая Леонардо да Винчи Мона Лиза (Джоконда)

Следующая - Лекарственные растения

Пересечение множеств презентация к уроку по математике (3 класс) по теме 109

Теория графов 104

Презентация проектной работы по математике по теме Чертёжные инструменты 162

формула 100

Урок математики во 2 классе план-конспект урока по математике (2 класс) по теме 112

Восьмеричная система счисления 125

Переместительный закон сложения 106

Презентация по математике на темуМатематика и ПДД (5кл) 132

Открытый урок по Математике 2 класс план-конспект урока по математике (2 класс) 127

Весёлая геометрия 146

Задачи на движение.Скорость.Время.Расстояние. презентация к уроку по математике (4 класс) 55

Урок 5 Признаки предметов 38

Дидактическая игра Вычисление расстояния по рисунку 128

Внеклассное занятие по математике. 126

Многогранники 180

Презентация к уроку математике по теме: Музыкальная математика 117

Движение 10 класс 108

Шар. Сфера. 120

Презентация к доклад у Система подготовки к ГИА по математике 129

Итоги мониторинга по математике учащихся 6-х классов 2015 – 2016 уч.год 93

Целое уравнение и его корни 122

Технологическая карта урока математики Тема: Деление на 2 2 класс УМК Школа России план-конспект урока по математике (2 класс) 229

математика, 1 класс презентация к уроку по математике (1 класс) по теме 105

Презентация по математике по теме Решение уравнений(5 класс) 127

Что такое findslide.org?

Обратная связь

Презентация на тему Неравенства и их системы

Содержание

Слайд 2 1)Определение 2) Виды 3) Свойства

числовых неравенств 4) Основные свойства неравенств 4) Типы 5)

Слайд 3 Запись вида а>в или а

Слайд 4 Неравенства вида а≥в, а≤в называются ……Неравенства вида а>в,

а

Слайд 5 1) Если а>в, то вв, в>с, то

а>с.3) Если а>в, с-любое число, то а+с>в+с.4) Если а>в,

Слайд 6 1). Любой член неравенства можно переносить из одной

части неравенства в другую, изменив его знак на противоположный,

Слайд 7 ЛИНЕЙНЫЕКВАДРАТНЫЕРАЦИОНАЛЬНЫЕИРРАЦИОНАЛЬНЫЕНЕРАВЕНСТВА

Слайд 8 I)I)Линейное неравенство 2х+4≥6; 2х≥-2; х≥-1;

Слайд 9 Решить неравенства1) х+2≥2,5х-1;2)х- 0,25(х+4)+0,5(3х-1)>3;3)4)х²+х

Слайд 10 Найдите наименьшие целые числа, являющиеся решениями неравенств1)2(х-3)-1-3(х-2)-4(х+1)>0;2)0,2(2х+2)-0,5(х-1)

натуральные числа, являющиеся решениями неравенства3х-3

Слайд 11 II)II)Квадратные неравенстваСпособы решения:Графический С С применением систем неравенствМетод

интервалов

Слайд 12 1.1)Метод интервалов(для решения квадратного уравнения)

ах²+вх+с>01) Разложим данный многочлен на множители,

Слайд 13 x²+x-6=0; (х-2)(х+3)=0; Ответ: (-∞;-3)v(2;+∞)

х + 2 -3 + -

Слайд 14 Решение неравенства методом интервалов1) х(х+7)≥0;2)(х-1)(х+2)≤0;3)х-х²+20;5)х(х+2)

Слайд 15 Домашняя работа:Сборник 1).стр. 109 № 128-131Сборник 2).стр.111 №3.8-3.10;