Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему

Содержание

2. АннотацияДанная методическая разработкапредставляет собой описание опыта автора, связанного с применениемтехнологии обучения геометрии сиспользованием интерактивнойгеометрической среды.
3. ЦЕЛЬ УРОКАознакомление учащихся с историей и формулировкой
4. ПЛАН УРОКА . 1. Организационный момент, актуализация
5. ОРГАНИЗАЦИОННЫЙ МОМЕНТ И АКТУАЛИЗАЦИЯ ЗНАНИЙ
6. Пифагор .(Около 569г. – около 475 г.
7. История возникновения теоремы ПифагораТеорема Пифагора- важнейшее утверждение
8. За 2000 лет
9. Пифагор или кто-то из его учеников нашли
10. Евклид о теореме ПифагораОдну из древнейших формулировок
11. Легенда о теоремеА. ШамиссоОбильно было жертвоприношенье Богам
12. Теорема ПифагораЕсли дан нам треугольникИ при том
13. АbсаСВс² = а² + b ² В
14. Доказательство 1.АСВДЕbасbас1) Достроим до трапеции.2) АВЕ=180-(АВС+ ДВЕ)==180-(
15. Доказательство 2аbсbааbаbсссS =(а + b)² = а
16. Практическое применение теоремы Пифагора. С помощью
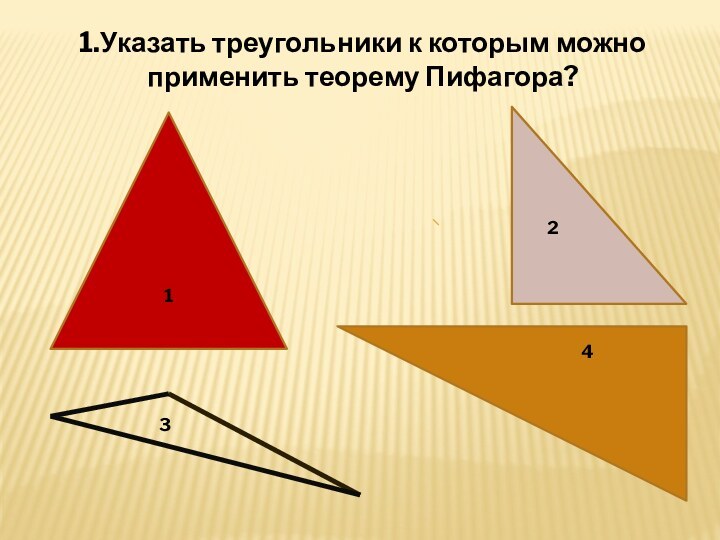
17. 12341.Указать треугольники к которым можно применить теорему Пифагора?
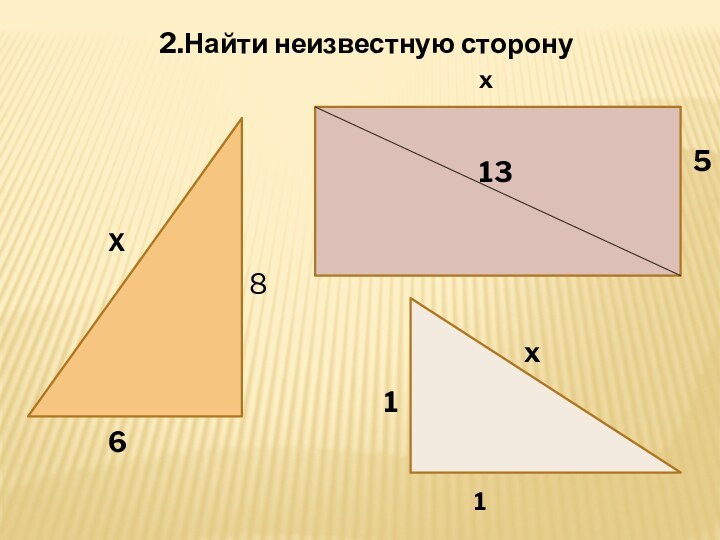
18. 6X8x511x2.Найти неизвестную сторону13
19. 68АD3.Решение задач по готовым чертежамСоставьте по рисункам,
20. Тест ОТВЕТИТЬ ПРАВИЛЬНО НА ВОПРОС ТЕСТА ,
21. 2. КАКОЕ ИЗ РАВЕНСТВ ВЫРАЖАЕТ ТЕОРЕМУ ПИФАГОРА
22. 2. КАКОЕ ИЗ РАВЕНСТВ ВЫРАЖАЕТ ТЕОРЕМУ ПИФАГОРА
23. 3.ЧЕМУ РАВНА ГИПОТЕНУЗА АВ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА
24. 3.ЧЕМУ РАВНА ГИПОТЕНУЗА АВ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА АВС
25. 3.ЧЕМУ РАВНА ГИПОТЕНУЗА АВ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА АВС
26. 4.ЧЕМУ РАВЕН КАТЕТ МР ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА АВС
27. 4.ЧЕМУ РАВЕН КАТЕТ МР ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА АВС
28. 4.ЧЕМУ РАВЕН КАТЕТ МР ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА АВС
29. 4.ЧЕМУ РАВЕН КАТЕТ МР ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА АВС
30. 5.ЧЕМУ РАВНА ДИАГОНАЛЬ КВАДРАТА АВСДА)√3; Б) 3√2; В)6; Г) среди данных ответов правильного нет.3АВСД4 балла
31. 5.ЧЕМУ РАВНА ДИАГОНАЛЬ КВАДРАТА АВСДА) √3; Б)
32. 5.ЧЕМУ РАВНА ДИАГОНАЛЬ КВАДРАТА АВСДА)√3; Б) 3√2; В)6;Г) среди данных ответов правильного нет.3АВСД2 балла
33. 5.ЧЕМУ РАВНА ДИАГОНАЛЬ КВАДРАТА
34. 5.ЧЕМУ РАВНА ДИАГОНАЛЬ КВАДРАТА
35. 5 балловМОЛОДЕЦ!ДАЛЕЕ
36. 4 баллаХОРОШО!ДАЛЕЕ
37. 3 баллаДАЛЕЕ
38. 2 баллаДАЛЕЕ
39. Пребудет вечной истина, как скороВсе познает слабый
40. Подведение итогов урокаДомашнее задание:1.Теорема Пифагора. Подготовить
41. Скачать презентацию
42. Похожие презентации

АннотацияДанная методическая разработкапредставляет собой описание опыта автора, связанного с применениемтехнологии обучения геометрии сиспользованием интерактивнойгеометрической среды.

УРОК с применением новой геометрической средына тему: «Теорема Пифагора»Бочарова Светлана АлександровнаМБОУ «Каргинская

ЦЕЛЬ УРОКАознакомление учащихся с историей и формулировкой теоремы Пифагора.подведение их к открытию

ПЛАН УРОКА . 1. Организационный момент, актуализация знаний.2. Знакомство с историей теоремы

ОРГАНИЗАЦИОННЫЙ МОМЕНТ И АКТУАЛИЗАЦИЯ ЗНАНИЙ

Пифагор .(Около 569г. – около 475 г. до н.э.)Пифагор родился около 570

История возникновения теоремы ПифагораТеорема Пифагора- важнейшее утверждение геометрии. Обычно открытие этого утверждения

За 2000 лет до н.э. древние египтяне знали

Пифагор или кто-то из его учеников нашли формулы для отыскания бесконечного множества

Евклид о теореме ПифагораОдну из древнейших формулировок и доказательств данной теоремы изложил

Легенда о теоремеА. ШамиссоОбильно было жертвоприношенье Богам от Пифагора. Сто быков

Теорема ПифагораЕсли дан нам треугольникИ при том с прямым углом,То квадрат гипотенузыМы

АbсаСВс² = а² + b ² В прямоугольном треугольнике квадрат гипотенузы

Доказательство 1.АСВДЕbасbас1) Достроим до трапеции.2) АВЕ=180-(АВС+ ДВЕ)==180-( АВС+САВ)=180-90=90;3)SАВЕ =(с*с)/2=с²/2;4)SСАЕД= аb/2 +с²/2+аb/2=(2аb+с²)/2;5)SСАЕД=(а +

Доказательство 2аbсbааbаbсссS =(а + b)² = а ² +2аb+ b²Но площадь квадрата

Практическое применение теоремы Пифагора. С помощью теоремы Пифагора решают разнообразные практические

12341.Указать треугольники к которым можно применить теорему Пифагора?

68АD3.Решение задач по готовым чертежамСоставьте по рисункам, используя теорему Пифагора, если это

Тест ОТВЕТИТЬ ПРАВИЛЬНО НА ВОПРОС ТЕСТА , НАЖАВ НА ПРАВИЛЬНЫЙ ОТВЕТ 1

2. КАКОЕ ИЗ РАВЕНСТВ ВЫРАЖАЕТ ТЕОРЕМУ ПИФАГОРА ( а, в, с- стороны

2. КАКОЕ ИЗ РАВЕНСТВ ВЫРАЖАЕТ ТЕОРЕМУ ПИФАГОРА ( а, в, с-

3.ЧЕМУ РАВНА ГИПОТЕНУЗА АВ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА АВС ( ∠С = 900)А)

3.ЧЕМУ РАВНА ГИПОТЕНУЗА АВ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА АВС ( ∠С = 900)А) 7;

4.ЧЕМУ РАВЕН КАТЕТ МР ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА АВС (∠С = 900)А) 12; Б)

5.ЧЕМУ РАВНА ДИАГОНАЛЬ КВАДРАТА АВСДА)√3; Б) 3√2; В)6; Г) среди данных ответов правильного нет.3АВСД4 балла

5.ЧЕМУ РАВНА ДИАГОНАЛЬ КВАДРАТА АВСДА) √3; Б) 3 √2; В)6; Г) среди

5.ЧЕМУ РАВНА ДИАГОНАЛЬ КВАДРАТА АВСДА)√3; Б) 3√2; В)6;Г) среди данных ответов правильного нет.3АВСД2 балла

5.ЧЕМУ РАВНА ДИАГОНАЛЬ КВАДРАТА АВСДА) √3; Б) 3√2; В)6;

Пребудет вечной истина, как скороВсе познает слабый человек!И ныне теорема ПифагораВерна, как

Подведение итогов урокаДомашнее задание:1.Теорема Пифагора. Подготовить сообщения: «Я знаю интересные

Литература:Геометрия, 7-9 : Учеб. для общеобразовательных учреждений/ Л.С.Атанасян, В.Ф.Бутузов,

Слайды презентации

Слайд 2 Аннотация
Данная методическая разработка
представляет собой описание опыта
автора, связанного

с применением
технологии обучения геометрии с
использованием интерактивной
геометрической среды.

Слайд 3 ЦЕЛЬ УРОКА
ознакомление учащихся с историей и формулировкой теоремы

ЦЕЛЬ УРОКАознакомление учащихся с историей и формулировкой теоремы Пифагора.подведение их к

Пифагора.
подведение их к открытию и доказательству её.
формирование первичных умений,

связанных с теоремой Пифагора.

Оборудование ПК, мультимедиа-проектор.
Место проведения урока: кабинет математики, оснащенный компьютерами.

Слайд 4 ПЛАН УРОКА

.
1. Организационный момент, актуализация знаний.
2.

ПЛАН УРОКА . 1. Организационный момент, актуализация знаний.2. Знакомство с историей

Знакомство с историей теоремы Пифагора в стихах, в современной

интерпретации.
3.Доказательство теоремы.
4. Практическое применение теоремы Пифагора.
5. Выполнение теста
6. Подведение итогов урока.

Слайд 5 ОРГАНИЗАЦИОННЫЙ МОМЕНТ
И АКТУАЛИЗАЦИЯ ЗНАНИЙ

Слайд 6 Пифагор
.
(Около 569г. – около 475 г. до н.э.)
Пифагор

Пифагор .(Около 569г. – около 475 г. до н.э.)Пифагор родился около

родился около 570 г. до н. э. на острове

Самосе. По античным свидетельствам он был красив и обладал незаурядными способностями.
    548 г. до н.э. он прибыл в Навкратис. Научившись всему, что дали ему жрецы, он отправился на родину в Элладу.
Во время путешествия был захвачен в плен царем Вавилона.
   В 530 г. до н.э. сбежал из плена на родину. Там создает «пифагорейскую» школу в которой рассматривались четыре науки: арифметика, музыка(гармония), геометрия и астрономия с астрологией.
   Приблизительно в 510 г. до н.э. Покончил жизнь самоубийством.

Слайд 7 История возникновения теоремы Пифагора
Теорема Пифагора- важнейшее утверждение геометрии.

История возникновения теоремы ПифагораТеорема Пифагора- важнейшее утверждение геометрии. Обычно открытие этого

Обычно открытие этого утверждения приписывают древнегреческому философу и математику

Пифагору. Но изучение вавилонских таблиц и древних китайских рукописей показало, что данное утверждение было известно задолго до Пифагора. Заслуга Пифагора состояла в том, что он открыл доказательство этой теоремы.

Слайд 8

За 2000 лет до

За 2000 лет до н.э. древние египтяне знали о

н.э. древние египтяне знали о том, что треугольник со

сторонами 3, 4, 5 есть прямоугольный и пользовались этим соотношением для построения прямых углов при сооружении зданий.

В Древнем Китае за 1100 лет до н.э. было установлено наглядное доказательство данной теоремы, содержащееся в древнейшем китайском трактате «Чжоу-би». .

Теорема Пифагора
в Китае

Теорема Пифагора
в Египте

Слайд 9 Пифагор или кто-то из его учеников
нашли формулы

Пифагор или кто-то из его учеников нашли формулы для отыскания бесконечного

для отыскания
бесконечного множества таких троек:
a =

2mn, b = m2– n2, c =m2 + n2,
где m и n –любые натуральные числа,
такие, что m>n.

Кроме этого к нам от Пифагора
пришли следующие термины
«квадрат» для чисел n2 и «куб» для чисел n3.

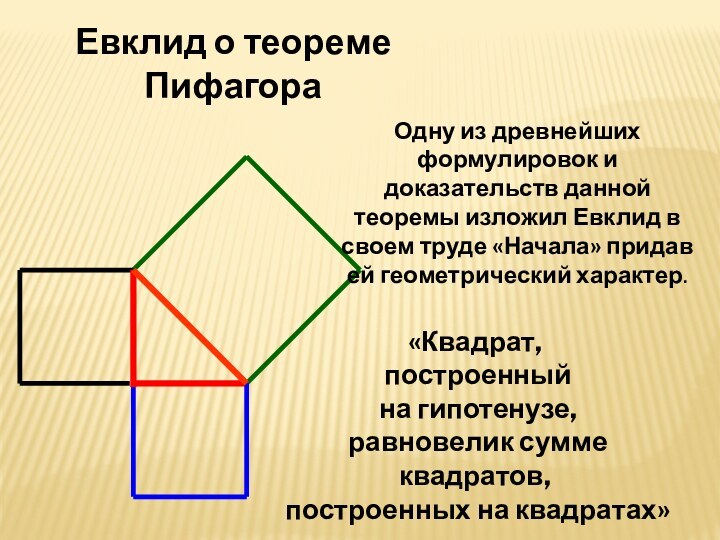
Слайд 10 Евклид о теореме Пифагора
Одну из древнейших формулировок и

Евклид о теореме ПифагораОдну из древнейших формулировок и доказательств данной теоремы

доказательств данной теоремы изложил Евклид в своем труде «Начала»

придав ей геометрический характер.

«Квадрат,
построенный
на гипотенузе,
равновелик сумме квадратов,
построенных на квадратах»

Слайд 11 Легенда о теореме
А. Шамиссо
Обильно было жертвоприношенье
Богам от

Пифагора. Сто быков
Он отдал на закланье и

сожженье
За света луч, пришедший с облаков.

Поэтому всегда с тех пор, чуть
истина рождается на свет, быки
ревут, ее почуя, вслед.

Они не в силах свету помешать,
А могут лишь, закрыв глаза, дрожать
От страха, что вселил в них Пифагор.

Слайд 12 Теорема Пифагора
Если дан нам треугольник
И при том с

Теорема ПифагораЕсли дан нам треугольникИ при том с прямым углом,То квадрат

прямым углом,
То квадрат гипотенузы
Мы всегда легко найдем:
Катеты в квадрат

возводим,
Сумму степеней находим-
И таким простым путем
К результату мы придем.

катет

гипотенуза

Слайд 13 А
b
с
а
С
В
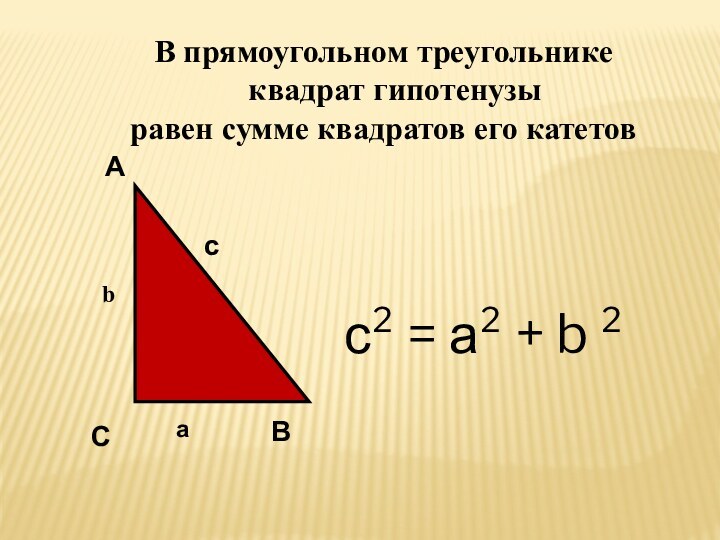
с² = а² + b ²
В прямоугольном

АbсаСВс² = а² + b ² В прямоугольном треугольнике квадрат

треугольнике
квадрат гипотенузы
равен сумме квадратов его

катетов

Слайд 14 Доказательство 1.
А
С
В
Д
Е
b
а
с
b
а
с
1) Достроим до трапеции.
2) АВЕ=180-(АВС+ ДВЕ)=
=180-( АВС+САВ)=180-90=90;
3)SАВЕ

=(сс)/2=с²/2;
4)SСАЕД= аb/2 +с²/2+аb/2=(2аb+с²)/2;
5)SСАЕД=(а + b)/2 (а + b)=(а

+ b)²/2;

6) (2аb+с²)/2=(а²+2аb+b²)/2;

7) с²=а²+b².

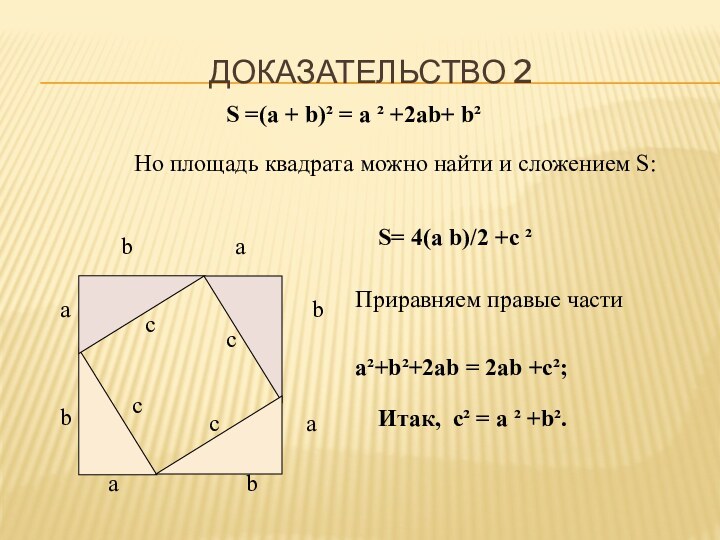
Слайд 15 Доказательство 2
а
b
с
b
а
а
b
а
b
с
с
с
S =(а + b)² = а ²

Доказательство 2аbсbааbаbсссS =(а + b)² = а ² +2аb+ b²Но площадь

+2аb+ b²
Но площадь квадрата можно найти и сложением S:
S=

4(а b)/2 +с ²

Приравняем правые части

а²+b²+2аb = 2аb +с²;

Итак, с² = а ² +b².

Слайд 16 Практическое применение
теоремы Пифагора.
С помощью теоремы

Пифагора решают разнообразные практические задачи:
-нахождение элементов прямоугольного, равнобедренного, равностороннего

треугольников, диагоналей квадрата, прямоугольника;
-вычисление расстояния между точками;
Теорема Пифагора позволяет:
устанавливать соотношения между элементами правильных многоугольников;
доказывать многие теоремы;
выводить различные формулы, решать алгебраические задачи.

Слайд 17 1
2
3
4
1.Указать треугольники к которым можно применить теорему Пифагора?

Слайд 18 6
X
8
x
5
1
1
x
2.Найти неизвестную сторону
13

Слайд 19 6
8
А
D
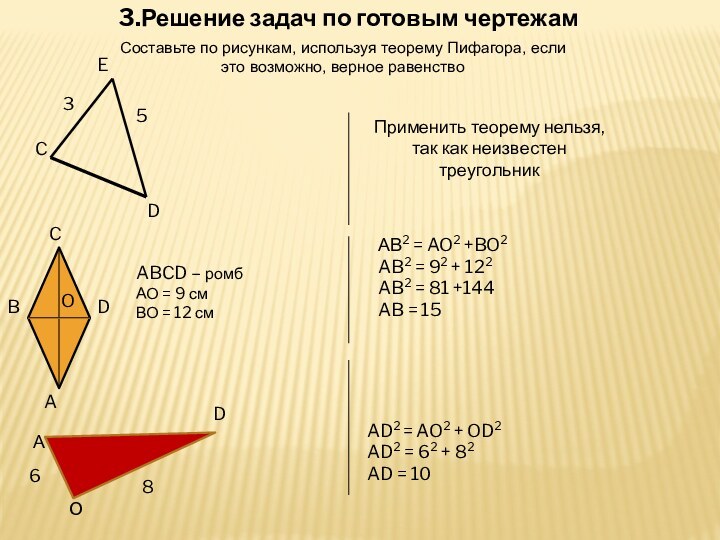
3.Решение задач по готовым чертежам
Составьте по рисункам, используя

68АD3.Решение задач по готовым чертежамСоставьте по рисункам, используя теорему Пифагора, если

теорему Пифагора, если это возможно, верное равенство
5
3
C
D
E
A
D
B
C
O
ABCD – ромб
АО

= 9 см
ВО = 12 см

AD2 = AO2 + OD2
AD2 = 62 + 82
AD = 10

Применить теорему нельзя, так как неизвестен треугольник

АВ2 = AO2 +BO2
AB2 = 92 + 122
AB2 = 81 +144
AB = 15

Слайд 20 Тест
ОТВЕТИТЬ ПРАВИЛЬНО НА ВОПРОС ТЕСТА , НАЖАВ

Тест ОТВЕТИТЬ ПРАВИЛЬНО НА ВОПРОС ТЕСТА , НАЖАВ НА ПРАВИЛЬНЫЙ ОТВЕТ

НА ПРАВИЛЬНЫЙ ОТВЕТ 1 ВОПРОСА И Т.Д.
КАКОЕ ИЗ УТВЕРЖДЕНИЙ

ЯВЛЯЕТСЯ ТЕОРЕМОЙ ПИФАГОРА
А) в любом треугольнике квадрат гипотенузы равен сумме квадратов катетов;
Б) в прямоугольном треугольнике квадрат катета равен сумме квадратов другого катета и гипотенузы;
В) в прямоугольном треугольнике гипотенуза равна сумме катетов;
Г) в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов?

Слайд 21 2. КАКОЕ ИЗ РАВЕНСТВ ВЫРАЖАЕТ ТЕОРЕМУ ПИФАГОРА (

а, в, с- стороны прямоугольного треугольника?)

А ) а² = в² + с²;

B) в² = а² + с²;

Б) с² = а² +в²;

1 балл

Г) с = а + в

Слайд 22 2. КАКОЕ ИЗ РАВЕНСТВ ВЫРАЖАЕТ ТЕОРЕМУ ПИФАГОРА

( а, в, с- стороны прямоугольного треугольника)?
О баллов
Г)

с = а + b

А) а² = b² + с²;

Б) с² = а² + b²;

В) b² = а² + с²;

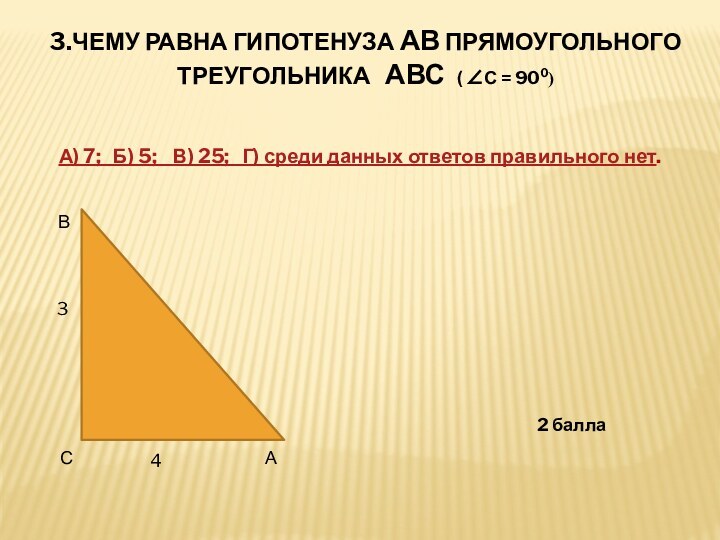
Слайд 23 3.ЧЕМУ РАВНА ГИПОТЕНУЗА АВ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА АВС

( ∠С = 900)
А) 7; Б) 5;

В) 25; Г) среди данных ответов правильного нет.

2 балла

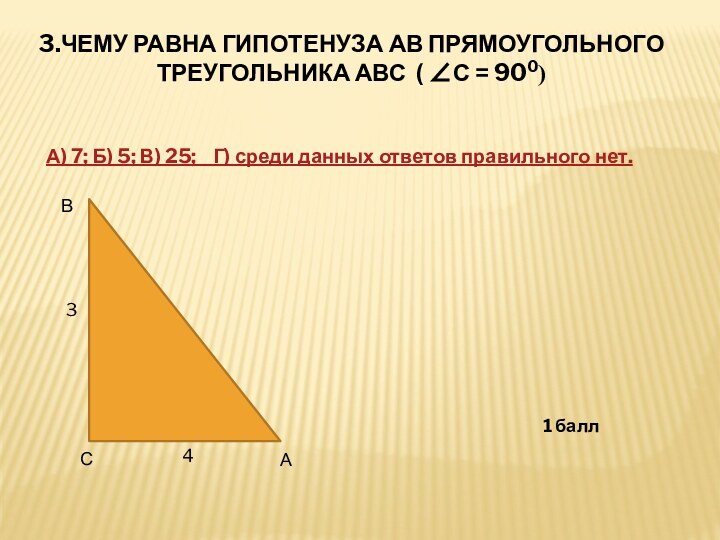
Слайд 24 3.ЧЕМУ РАВНА ГИПОТЕНУЗА АВ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА АВС (

∠С = 900)
А) 7; Б) 5; В) 25;

Г) среди данных ответов правильного нет.

1 балл

Слайд 25 3.ЧЕМУ РАВНА ГИПОТЕНУЗА АВ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА АВС (

∠С = 900)
А) 7; Б) 5; В) 25;

Г) среди данных ответов правильного нет.

О баллов

Слайд 26 4.ЧЕМУ РАВЕН КАТЕТ МР ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА АВС (∠С

4.ЧЕМУ РАВЕН КАТЕТ МР ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА АВС (∠С = 900)А) 12;

= 900)

А) 12; Б) 8; В) 18; Г)

среди данных ответов правильных нет.

3 балла

Слайд 27 4.ЧЕМУ РАВЕН КАТЕТ МР ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА АВС (∠С

= 900)

А) 12; Б) 8; В) 18; Г)

среди данных ответов правильных нет.

2 балла

Слайд 28 4.ЧЕМУ РАВЕН КАТЕТ МР ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА АВС (∠С

= 900)

А) 12; Б) 8; В) 18; Г)

среди данных ответов правильных нет.

1 балл

Слайд 29 4.ЧЕМУ РАВЕН КАТЕТ МР ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА АВС (∠С

= 900)

А) 12; Б) 8; В) 18;

Г) среди данных ответов правильного нет.

0 баллов

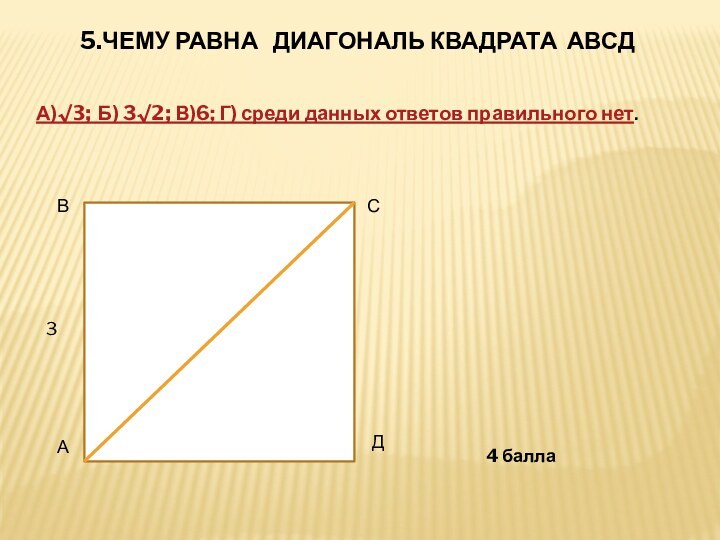
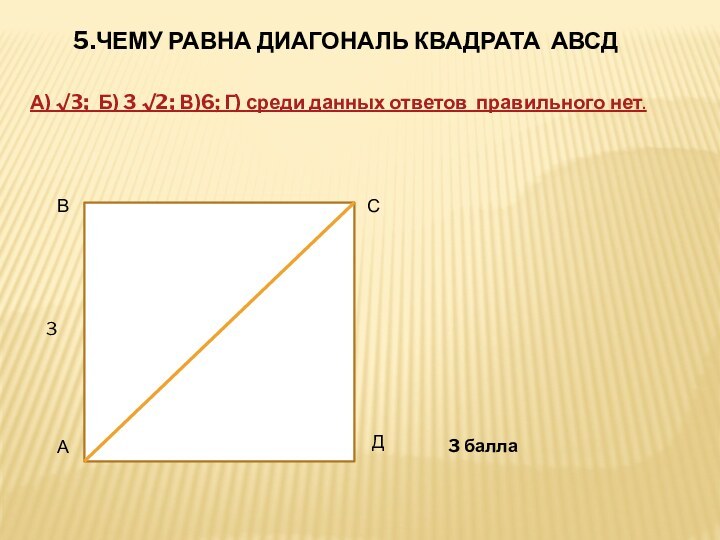
Слайд 30 5.ЧЕМУ РАВНА ДИАГОНАЛЬ КВАДРАТА АВСД
А)√3; Б) 3√2;

В)6; Г) среди данных ответов правильного нет.
3
А
В
С
Д
4 балла

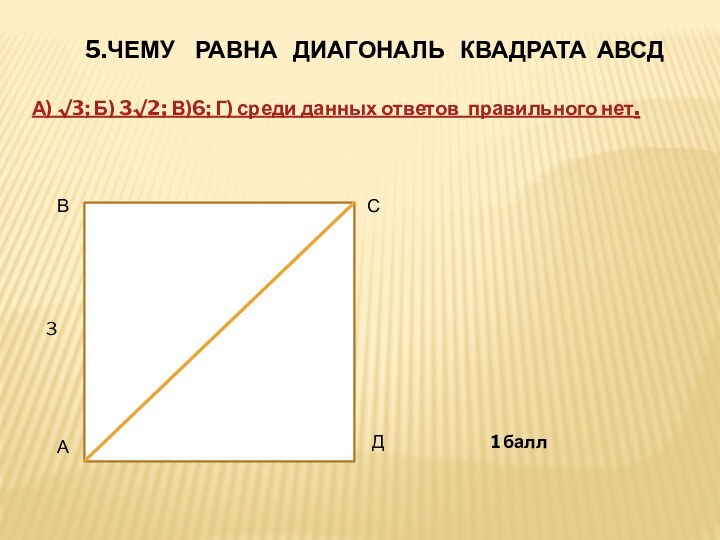
Слайд 31 5.ЧЕМУ РАВНА ДИАГОНАЛЬ КВАДРАТА АВСД
А) √3; Б) 3

√2; В)6; Г) среди данных ответов правильного нет.
3
А
В
С
Д
3 балла

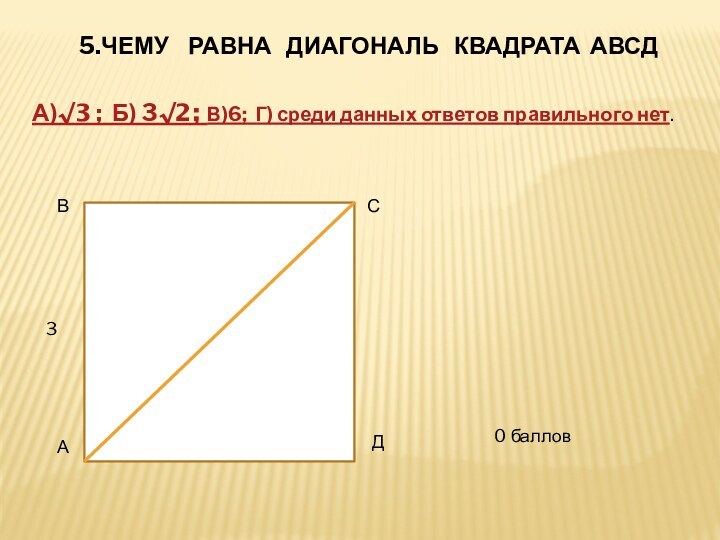
Слайд 32 5.ЧЕМУ РАВНА ДИАГОНАЛЬ КВАДРАТА АВСД
А)√3; Б) 3√2; В)6;Г)

среди данных ответов правильного нет.
3
А
В
С
Д
2 балла

Слайд 33 5.ЧЕМУ РАВНА ДИАГОНАЛЬ КВАДРАТА АВСД
А)

√3; Б) 3√2; В)6; Г) среди данных ответов правильного

нет.

1 балл

Слайд 34 5.ЧЕМУ РАВНА ДИАГОНАЛЬ КВАДРАТА АВСД
А)√3

; Б) 3√2; В)6; Г) среди данных ответов правильного

нет.

0 баллов

Слайд 35 5 баллов
МОЛОДЕЦ!
ДАЛЕЕ

Слайд 36 4 балла
ХОРОШО!

ДАЛЕЕ

Слайд 37 3 балла

ДАЛЕЕ

Слайд 38 2 балла
ДАЛЕЕ

Слайд 39 Пребудет вечной истина, как скоро
Все познает слабый человек!
И

Пребудет вечной истина, как скороВсе познает слабый человек!И ныне теорема ПифагораВерна,

ныне теорема Пифагора
Верна, как и в его далекий век.
Немецкий

писатель-романист XIX века
А. Шамисо.

сообщения: «Я знаю интересные
сведения из

жизни Пифагора»

2. №483, из учебника Геометрия, 7-9 : Учеб.
для общеобразовательных учреждений
Л.С. Атанасян, В.Ф.Бутузов, С.Б.Кадомцев
и др.

3. № 32.1 Задачи по геометрии для 7-11
классов. Б.Зив. В.М.Мейлер.