аргументом является вещественная переменная t.
Пусть на вход некоторого оператора,
преобразующего сигнал подается функция x(t) , а выходе получаем новый сигнал y(t). Мы рассматриваем поведение объекта на некотором интервале времени, то есть параметры представляют собой функции от времени на этом интерва-ле. Выходной параметр y(t) зависит от входного параметра, то есть от функции x(t), эта зависимость задается оператором преобразования.
Мы рассматриваем поведение объекта на некотором интервале времени, то есть параметры представляют собой функции от времени на этом интервале.
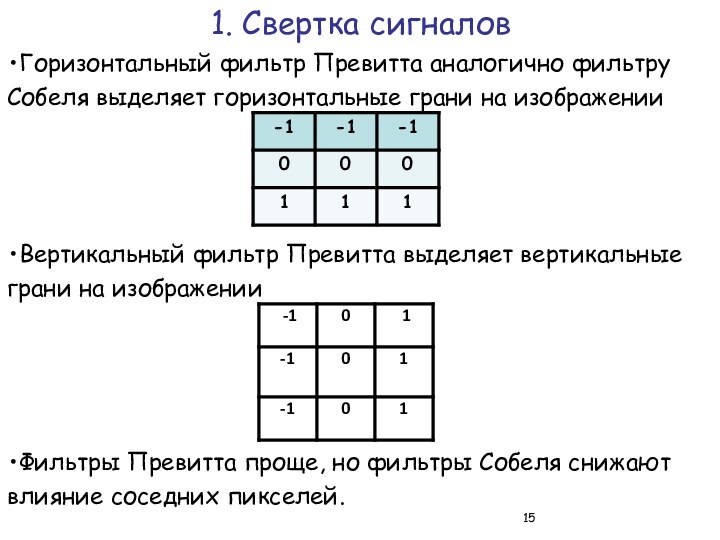
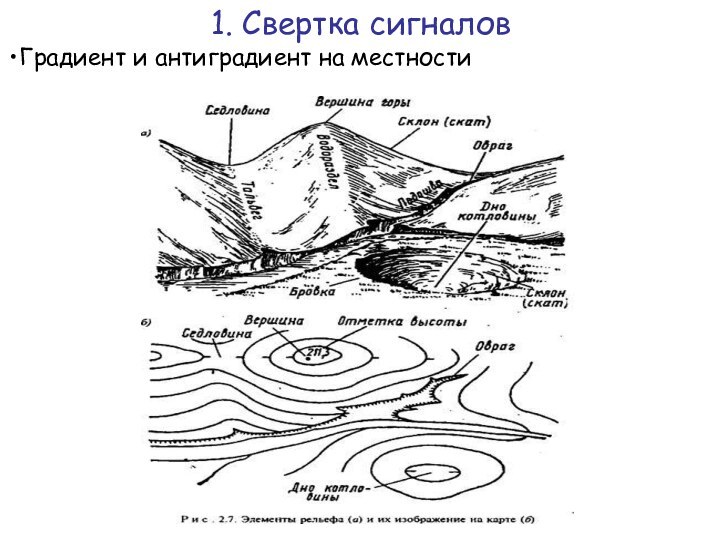
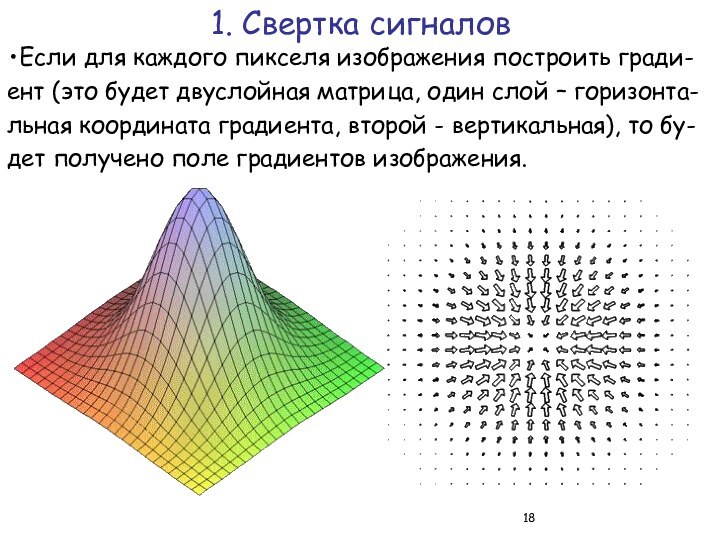
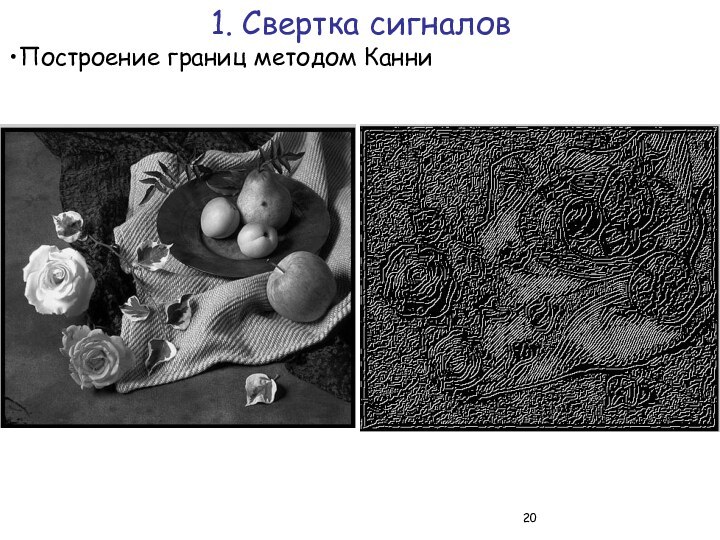
1. Свертка сигналов


![Оператор свертки Преобразование будем записывать в видеy(t) = F[x(t)], F переводит функции x(t) в](/img/tmb/15/1415855/e945e9d5ebdc208c987fab610906cff1-720x.jpg)