- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Основные математические положения, применяемые для анализа и построения статистической модели
Содержание
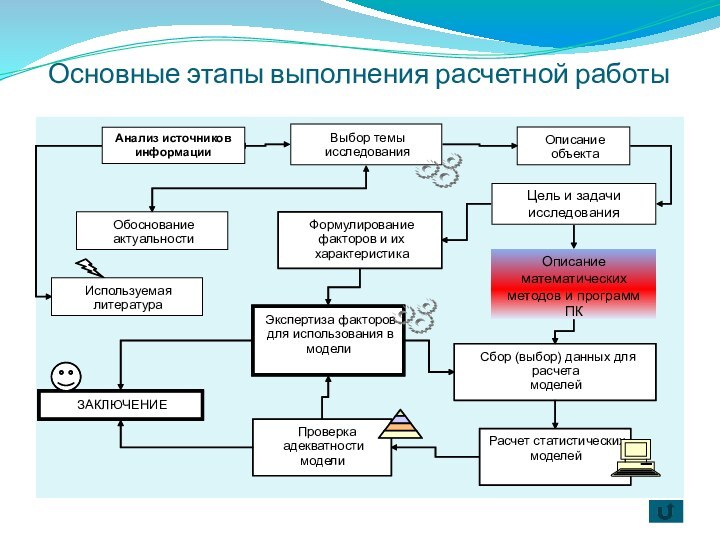
- 2. Основные этапы выполнения расчетной работы Анализ источников информации
- 3. «Тем, кто понимает суть регрессии и корреляции,
- 4. перед исследователями всегда стояла задача достоверного отображения
- 5. Корреляционный анализ. ИсторияЕще Гиппократ (греческий врач и
- 6. Корреляционный анализ. ИсторияТак современные логистические исследования, транспортных
- 7. Корреляционный анализ. ИсторияЭтой цели служит математическое понятие
- 8. Примеры элементарных функций:Причина таких «исключений» в том,
- 9. Корреляционный анализ. ИсторияОтсюда зависимость между величинами приобретает
- 10. Корреляционный анализ. ИсторияСлово «статистика» приходит от латинского
- 11. Корреляционный анализ. ОсновыКорреляция применяется при изучении экспериментальных
- 12. Корреляционный анализ. ОсновыСовокупность точек на плоскости создает
- 13. Корреляционный анализ. Основыгде xi, yi – значения
- 14. Корреляционный анализ. ОсновыЕсли коэффициент корреляции равен 0
- 15. Корреляционный анализ. ОсновыЕсли коэффициент корреляции принимает максимально
- 16. Корреляционный анализ. ОсновыЕсли В промежуточных случаях
- 17. Корреляционный анализ. ОсновыТолько по величине коэффициентов корреляции
- 18. Регрессионный анализ. ПонятиеВ практических исследованиях возникает необходимость
- 19. Уравнение линейной регрессииОбычно признак Y рассматривается как
- 20. Уравнение линейной регрессииЛинии регрессии пересекаются в точке
- 21. Уравнение линейной регрессииУравнение регрессии тем лучше описывает
- 22. Основы теории регрессионного анализаПосле выбора гипотезы о
- 23. Основы теории регрессионного анализаНа практике это равенство
- 24. Основы теории регрессионного анализаЕсли погрешности δi подчиняются
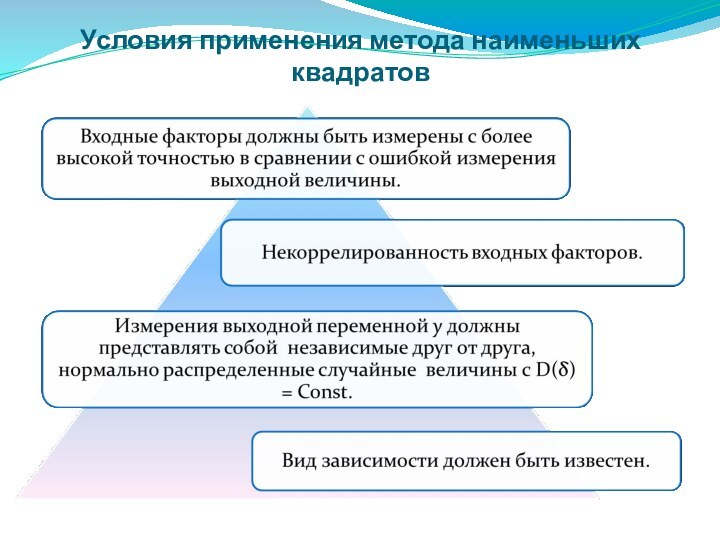
- 25. Условия применения метода наименьших квадратов
- 26. Нормальное распределение ГауссаНормальное распределение, также называемое гауссовым
- 27. Оценка качества полученной моделиМерой степени соответствия аппроксимирующей
- 28. Скачать презентацию
- 29. Похожие презентации























Слайд 3 «Тем, кто понимает суть регрессии и корреляции, советы
не нужны. Тем, кто не понимает, никакие советы не
помогут.»(Из книги Н. Джонсона и Ф. Лиона «Статистика и планирование эксперимента в технике и науке»).
Цель занятия:
Припоминание основ статистического моделирования (изученного на втором курсе в математике и статистике) процессов для анализа функционирования логистических объектов и на их основе выработки практических рекомендаций по совершенствованию исследуемых объектов.
Слайд 4 перед исследователями всегда стояла задача достоверного отображения объективно
существующих закономерностей в деятельности транспортного предприятия для конкретных условий,
в которых оно реализует свою деятельность (перевозку, складирование, хранение грузов и товаров) с обязательной количественной оценкой причинно-следственных взаимосвязей многообразия факторов.Описание проблемы:
Слайд 5
Корреляционный анализ. История
Еще Гиппократ (греческий врач и педагог,
чье имя связывается в представлении большинства людей со знаменитой
клятвой, которая символизирует высокие этические нормы европейской медицины)обратил внимание на то, что между телосложением и темпераментом людей, между строением их тела и предрасположенностью к заболеваниям существует определенная связь.
Слайд 6
Корреляционный анализ. История
Так современные логистические исследования, транспортных процессов
посвящены установлению закономерностей между достигаемым результатом и целым рядом
технических, технологических, эксплуатационных, психофизических, метеорологических и множество других характеристик (скорость перемещения объекта, производительность погрузки или разгрузки и отдельных звеньев объекта, показатели эксплуатационной надежности, объемы хранения и энергозатраты, связанные с функционированием объекта, и др.).При этом постоянно возникает вопрос о взаимосвязи отдельных признаков.
Слайд 7
Корреляционный анализ. История
Этой цели служит математическое понятие функции,
имеющее в виду случаи, когда определенному значению одной (независимой)
переменной Х, называемой аргументом, соответствует определенное значение другой (зависимой) переменной Y, называемой функцией. Однозначная зависимость между переменными величинами Y и X называется функциональной, т.е. Y = f(X).Например, в функции у = -2х+1 каждому значению х соответствует в определенное значение у.
В функции у = х2 каждому значению Y соответствует 2 определенных значения X. Графически это выглядит так (см. рисунок):
Слайд 8
Примеры элементарных функций:
Причина таких «исключений» в том, что
каждый признак, выражаясь математическим языком, является функцией многих переменных;
на его величине сказывается влияние и других факторов, в том числе и случайных, что вызывает варьирование признаков.Но такого рода однозначные или функциональные связи между переменными величинами встречаются кране редко.
Известно, что новый погрузочный механизм должен иметь большую производительность, чем морально и физически устаревший. Однако из такого правила бывают исключения.
Слайд 9
Корреляционный анализ. История
Отсюда зависимость между величинами приобретает не
функциональный, а статистический характер, когда определенному значению одного признака,
рассматриваемого в качестве независимой переменной, соответствует не одно и то же числовое значение, а целая гамма распределяемых в вариационный ряд числовых значений другого признака, который рассматриваемого в качестве независимой переменной. Такого рода зависимость между переменными величинами называется корреляционной или корреляцией.Термин «корреляция» происходит от лат. correlatio — соотношение, связь). При этом данный вид взаимосвязи между признаками проявляется в том, что при изменении одной из величин изменяется среднее значение другой.
Слайд 10
Корреляционный анализ. История
Слово «статистика» приходит от латинского слова
status (состояние), которое употреблялось в значении «политическое состояние». Отсюда
итальянские слова stato – государство и statista – знаток государств, отсюда также и немецкое слово Staat и английское state. В научный оборот слово «статистика» ввёл профессор Геттингенского университета Готфрид Ахенваль (1719 - 1772), понималось оно тогда как государствоведение.В первой половине 19 века возникло статистико-математическое направление данной науки. Среди представителей этого направления следует отметить бельгийского статистика Адольф Кетле (1796-1874 гг.) – основоположника учения о средних величинах.
Слайд 11
Корреляционный анализ. Основы
Корреляция применяется при изучении экспериментальных данных,
представляющих собой измеренные значения двух признаков.
В результате анализа
статистических данных или организованного эксперимента регистрируются различные значения случайных величин входных факторов - Xij и выходной - Yi в каждом из опытов, (где i,j принимает значения натуральных чисел, i - в пределах от =1 до m, j пределах от 1 до n,) имеющие некоторую взаимосвязь между последовательностями значений наблюдаемых величин.При этом корреляционную зависимость между признаками можно описывать разными способами: соответствие между аргументом и функцией может быть задано таблицей, формулой, графиком и т. д.
Слайд 12
Корреляционный анализ. Основы
Совокупность точек на плоскости создает общую
картину регрессии и позволяет построить некоторую усредненную кривую взаимосвязи
параметров.Корреляционной связью между случайными переменными величинами называется функциональная связь между средним арифметическим значений наблюдений за выходной переменной, соответствующих данному значению входной. Характер и выраженность такой связи устанавливают с помощью коэффициента корреляции, предложенного в 1846 году О. Браве.
Наиболее простой вариант корреляционной связи, описывается коэффициентом парной корреляции, предложенным Карлом Пирсоном 1884 году (английский математик, биолог, философ-позитивист):
Слайд 13
Корреляционный анализ. Основы
где xi, yi – значения наблюдаемых
входного и выходного параметров в i-том наблюдении;
x, y -
средние значения параметров x и y наблюдений;n - общее число наблюдений;
δx, δy - среднеквадратичные отклонения параметров x, y.
Среднеквадратичное отклонение параметра x определяется по известной формуле
Слайд 14
Корреляционный анализ. Основы
Если коэффициент корреляции равен 0 то
корреляция отсутствует – исследуемые параметры х и у не
связаны линейной зависимостью, и являются независимыми случайными величинами, но это не свидетельствует об отсутствии связи – она может быть нелинейной.Задача корреляционного анализа сводится к установлению направления и формы связи между признаками, измерению ее тесноты и к оценке достоверности выборочных показателей корреляции.
Корреляционная связь между признаками может быть линейной и криволинейной (нелинейной), положительной и отрицательной.
Величина коэффициента корреляции всегда заключена в пределах
Слайд 15
Корреляционный анализ. Основы
Если коэффициент корреляции принимает максимально возможные
значения 1 или -1 то между случайными величинами Х
и Y существует линейная функциональная зависимость (Y = а + вX). В этом случае говорят о полной корреляции.Если , то значения определяют точки, лежащие на прямой линии, имеющей положительный уклон – с увеличением аргумента функция увеличивается.
Если , то значения определяют точки, лежащие на прямой линии, имеющей отрицательный уклон – с увеличением аргумента функция уменьшается.
графическая интерпретация на рисунке.
Слайд 16
Корреляционный анализ. Основы
Если В промежуточных случаях
точки попадают в область, ограниченную некоторым эллипсом. При
этом, чем ближе расчетная величина к максимально возможной, тем уже эллипс и теснее экспериментальные значения группируются возле линии.Прямая корреляция отражает однотипность в изменении признаков: с увеличением (уменьшением) значений первого признака увеличиваются (уменьшается) значения и другого. Обратная корреляция указывает на увеличение первого признака при уменьшении второго или уменьшение первого признака при увеличении второго.
Слайд 17
Корреляционный анализ. Основы
Только по величине коэффициентов корреляции нельзя
судить о достоверности корреляционной связи между признаками. Этот параметр
зависит от числа степеней свободы k = n –2, где: n – число коррелируемых пар показателей Х и Y. Чем больше n, тем выше достоверность связи при одном и том же значении коэффициента корреляции. В практической деятельности, когда число коррелируемых пар признаков Х и Y не велико (n<=30), то при оценке зависимости между показателями используется следующую градацию:1) высокая степень взаимосвязи – значения коэффициента корреляции находится в пределах от 0,7 до 0,99;
2) средняя степень взаимосвязи – значения коэффициента корреляции находится в пределах от 0,5 до 0,69;
3) слабая степень взаимосвязи – значения коэффициента корреляции находится от 0,2 до 0,49.
Слайд 18
Регрессионный анализ. Понятие
В практических исследованиях возникает необходимость аппроксимировать
(описать приблизительно) диаграмму рассеяния математическим уравнением. То есть зависимость
между переменными величинами Y и Х можно выразить аналитически с помощью формул и уравнений и графически в виде точек в системе прямоугольных координат.График корреляционной зависимости строится по уравнениям функции и , которые называются регрессией.
Термин «регрессия» происходит от лат. regressio —
движение назад. В нашем случае — статистическая
зависимость среднего значения случайной величины
от значений другой случайной величины или нескольких случайных величин; введена Фрэнсисом Гальтоном
(английский статистик, психолог и антрополог; 1886).
Слайд 19
Уравнение линейной регрессии
Обычно признак Y рассматривается как функция
многих аргументов — x1, x2, x3, ...— и может
быть записана в виде: y = a + bx1 + cx2 + dx3 + ... , где: а, b, с и d — параметры уравнения, определяющие соотношение между аргументами и функцией.В практике учитываются не все, а лишь некоторые аргументы. В простейшем случае, как при описании линейной регрессии, всего один y = a + bx
В уравнении параметр а — свободный член; графически он представляет отрезок ординаты (у) в системе прямоугольных координат. Параметр b называется коэффициентом регрессии. С точки зрения аналитической геометрии b— угловой коэффициент, определяющий наклон линии регрессии по отношению к осям, координат.
Слайд 20
Уравнение линейной регрессии
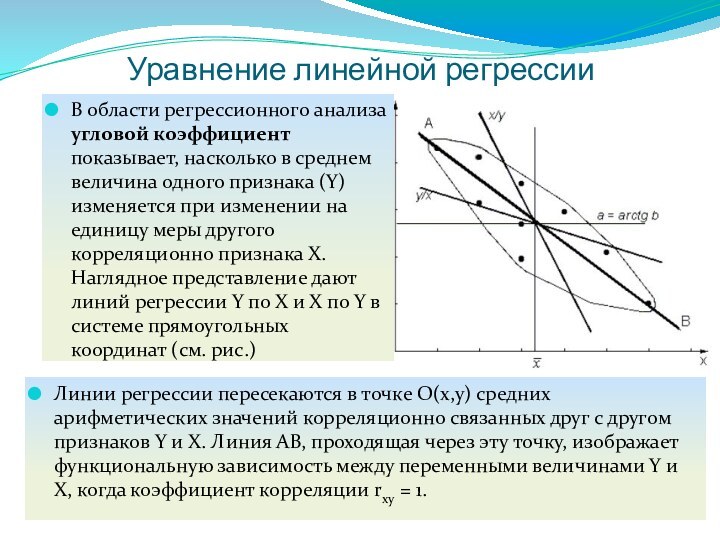
Линии регрессии пересекаются в точке О(х,у)
средних арифметических значений корреляционно связанных друг с другом признаков
Y и X. Линия АВ, проходящая через эту точку, изображает функциональную зависимость между переменными величинами Y и X, когда коэффициент корреляции rху = 1.В области регрессионного анализа угловой коэффициент показывает, насколько в среднем величина одного признака (Y) изменяется при изменении на единицу меры другого корреляционно признака X. Наглядное представление дают линий регрессии Y по Х и X по Y в системе прямоугольных координат (см. рис.)
Слайд 21
Уравнение линейной регрессии
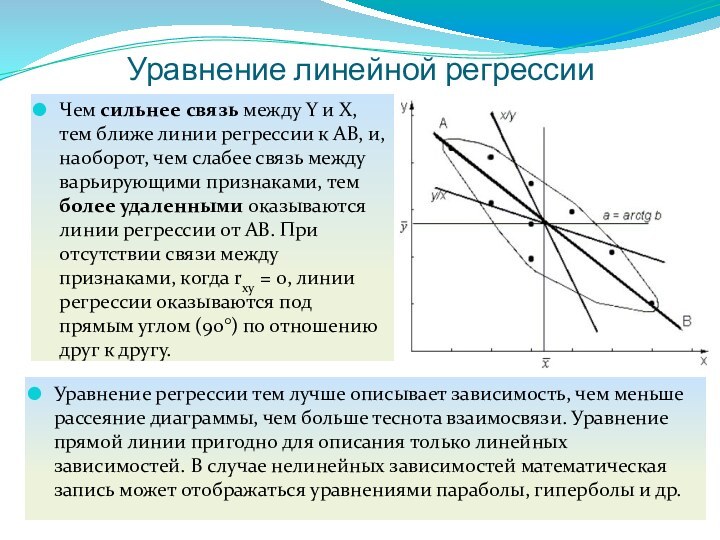
Уравнение регрессии тем лучше описывает зависимость,
чем меньше рассеяние диаграммы, чем больше теснота взаимосвязи. Уравнение
прямой линии пригодно для описания только линейных зависимостей. В случае нелинейных зависимостей математическая запись может отображаться уравнениями параболы, гиперболы и др.Чем сильнее связь между Y и X, тем ближе линии регрессии к АВ, и, наоборот, чем слабее связь между варьирующими признаками, тем более удаленными оказываются линии регрессии от АВ. При отсутствии связи между признаками, когда rху = 0, линии регрессии оказываются под прямым углом (90°) по отношению друг к другу.
Слайд 22
Основы теории регрессионного анализа
После выбора гипотезы о виде
зависимости между случайными величинами (вид уравнения), которым описывается модель
статистической связи, появляется необходимость нахождения параметров этого уравнения (свободного члена и коэффициентов).Эта задача решается с помощью регрессионного анализа. В общем случае из условия максимального приближения предполагаемой линии регрессии к точкам, отражающим опытные данные получается система нормальных уравнений. Для случая, когда все наблюдаемые значения за переменными x и y лежат точно на прямой линии, выполняется равенство:
yi – a0 – ai xi = 0,
Слайд 23
Основы теории регрессионного анализа
На практике это равенство нарушается
и для отдельных наблюдений появляется ошибка δi. Она определяется
разностью между измеренной и вычисляемой по уравнению регрессии значениями переменной y в i – ом опыте. Возникает задача нахождения коэффициентов уравнения, обеспечивающих минимальную ошибку δi.Теория вероятностей показывает, что лучшим приближением будет такая линия, для которой сумма квадратов расстояний от точек до кривой будет минимальной. Этот метод называется методом наименьших квадратов, разработан Гауссом и называется принципом выравнивания; критерием выравнивания
Слайд 24
Основы теории регрессионного анализа
Если погрешности δi подчиняются нормальному
закону распределения, минимум можно найти, приняв к нулю частные
производные по всем неизвестным:Q/ a0 = …= Q/ am = 0
После преобразования получается система нормальных уравнений. Решение этой системы позволяет найти искомые коэффициенты (a0, a1,…,am) регрессии.
Иоганн Карл Фри́дрих Га́усс немецкий математик, астроном и физик и философ. Считается величайшим математиков всех времён, «королём математиков». В 1794—95 годах осуществил первое применение к решению системы нормальных уравнений.
Слайд 26
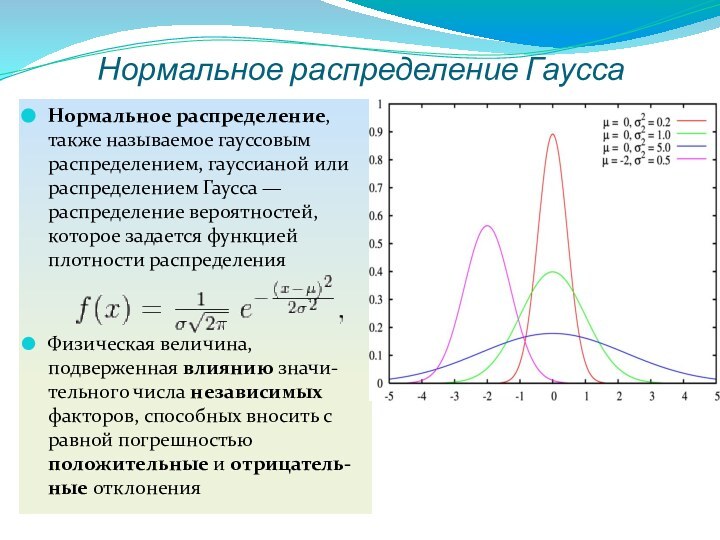
Нормальное распределение Гаусса
Нормальное распределение, также называемое гауссовым распределением,
гауссианой или распределением Гаусса — распределение вероятностей, которое задается
функцией плотности распределенияФизическая величина, подверженная влиянию значи-тельного числа независимых факторов, способных вносить с равной погрешностью положительные и отрицатель-ные отклонения
Слайд 27
Оценка качества полученной модели
Мерой степени соответствия аппроксимирующей регрессии
имеющимся значениям yi является коэффициент множественной корреляции (или детерминации):
Скорректированный
коэффициент множественной корреляции Коэффициенты изменяются в пределах 0…1; чем больше его значение, тем выше качество модели.
Еще одним критерием качества модели является статистика Jm
Качество полученной модели характеризуют минимальные значения Jm