Слайд 2
Цель занятия: Изучить основные понятия теории проверки статистических
гипотез
Тезисы лекции:
Статистическая гипотеза
Ошибки I и II рода
Статистический критерий
Критеческие точки
Основной
принцип проверки гипотез
Уровень статистической значимости
Этапы принятия статистического решения
Слайд 3
Литература.
Чудиновских В.Р.,Абдикадыр Ж.Н. Применение выборочного метода в медико-биологических
исследованиях., Учебное пособие. Астана 2012.
Чудиновских В.Р.,Абдикадыр Ж.Н., Применение
компьютерных программ для проверки статистических гипотез в медико-биологических исследованиях. Учебное пособие Астана 2014.
Койчибеков Б.К., Биостатистика. Учебное пособие-Издательство «Эверо», Алматы, 2014, 52 с
Койчибеков Б.К., Сорокина М.А., Букеева А.С., Такуадина А.И., Биостатистика в примерах и задачах: Учебно-метод.пособие/-Алматы, издательство «Эверо», Алматы, 2014.-80с.
Жидкова О.И., Медицинская статистика (конспект лекций), М. «Эксмо», 2007. Электронный учебник.
Вуколов Э.А. Основы статистического анализа. М.: ФОРУМ-2004.
Лобоцкая Н.Л. Высшая математика ,1987г. Глава 17
Лукьянова Е.А. Медицинская статистика.- М.: Изд. РУДН, 2002.
Слайд 4
1. Статистическая гипотеза
•Статистической называют гипотезу о виде неизвестного
распределения, или о параметрах известных распределений.
•Нулевой (основной) гипотезой называют
выдвинутую гипотезу H0.
•Конкурирующей (альтернативной) гипотезой называют гипотезу H1, которая противоречит нулевой.
•Например: H0: M(X)=M(Y); H1: M(X)≠M(Y).
Слайд 5
2. Ошибки I и II рода
Максимальная вероятность ошибки,
которую может себе позволить исследователь, принимая альтернативную гипотезу, называется
уровнем значимости и обозначается буквой α(альфа). Эту ошибку называют ошибкой первого I рода.
Также может возникнуть ошибка, если мы принимаем нулевую гипотезу, в то время как она верна, другими словами, не находим существующие различия. Это ошибка II рода, её вероятность обозначается буквой β
Величина (1- β) называется мощностью критерия- это способность критерия найти различия там, где они заведомо существуют.
Слайд 6
3. Статистический критерий
Для проверки нулевой гипотезы используют
специально подобранную
случайную величину, точное или приближенное распределение которой известно.
Статистическим критерием
(далее просто
критерием) называют случайную величину K,
которая служит для проверки нулевой гипотезы.
Слайд 7
Все критерии различия условно делятся на параметрические и
непараметрические критерии.
Критерий различия называется
параметрическим, если он основан на конкретном виде распределения генеральной совокупности (как правило нормальном) и использует параметр этой совокупности (средние, дисперсии и т.д.). Чаще всего в медико-биологических исследованиях применяется t-критерий Стьюдента, если оценивается различие средних двух выборок , и F- критерий Фишера, если оцениваются различия между двумя дисперсиям. Использование параметрических критериев статистики без предварительной проверки вида распределения может привести к определенным ошибкам в ходе проверки рабочей гипотезы.
Слайд 8
Критерий различия называется непараметрическим,
если критерий не базируется на предположении о виде распределения
и не использует параметры этой совокупности. Для анализа медико-биологических данных обычно используют критерий знаков, двухвыборочный критерий Вилкоксона, критерий Манна-Уйитни, критерий Ван дер Вардена, критерий Спирмена, выбор которых, хотя и не требует большого числа членов выборки и знаний, вида распределения, но все же зависит от целого ряда условий.
Слайд 9
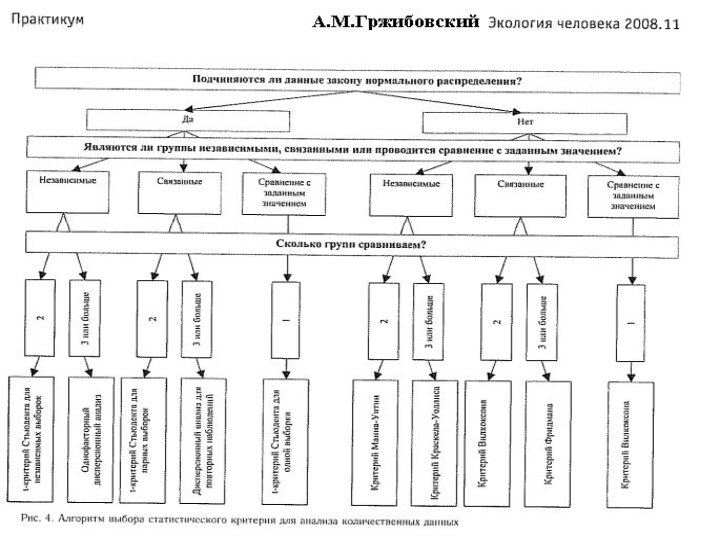
Прежде чем решить вопрос
о выборе статистического критерия необходимо определить тип собранных данных,
подчиняются ли данные нормальному закону распределения, являются ли группы данных зависимыми, связанными, сколько используется групп. Алгоритм выбора статистического критерия для анализа количественных данных представлен на рисунке.
Слайд 11
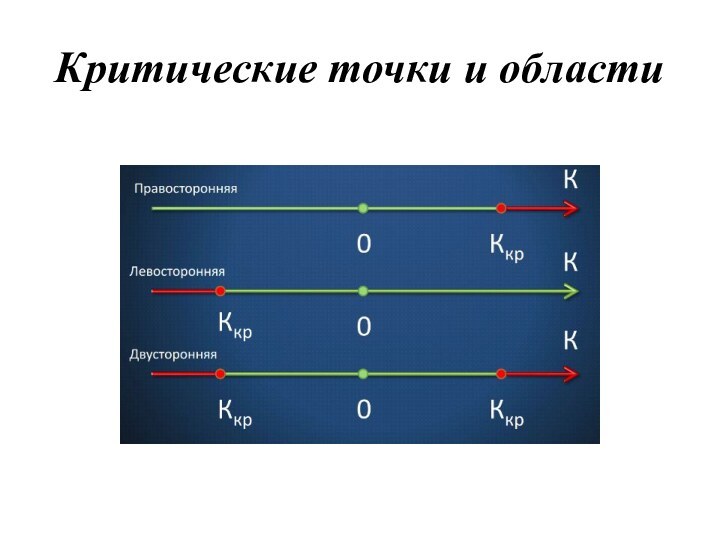
4. Критические точки
• Критической областью называют совокупность
значений
критерия, при которых гипотезу отвергают.
• Область принятия гипотезы (область
допустимых
значений) называют совокупность значений критерия, при которых гипотезу принимают.
• Критическими точками (границами, значениями,
Kкр) называют точки, отделяющие критическую
область от области принятия решений.
Слайд 13
Поиск критической точки
•Задается уровень значимости α (α=0.05)
• Для
левосторонней
P(KKкр)=α
• Для двусторонней
P(K
P(K>Kкр)=α/2
NB! Для каждого статистического критерия (К) уже найдена критическая точка (Ккр) для уровня значимости (α) и находится по таблицам или с помощью компьютерной программы
Слайд 14
5. Основной принцип проверки гипотез
• Если наблюдаемое значение
критерия принадлежит критической области, то гипотезу отвергают, если наблюдаемое
значение принадлежит области принятия гипотезы, то гипотезу принимают.
• Наблюдаемое критическое значение (Кнабл) – значение критерия рассчитанное по выборке
Слайд 15
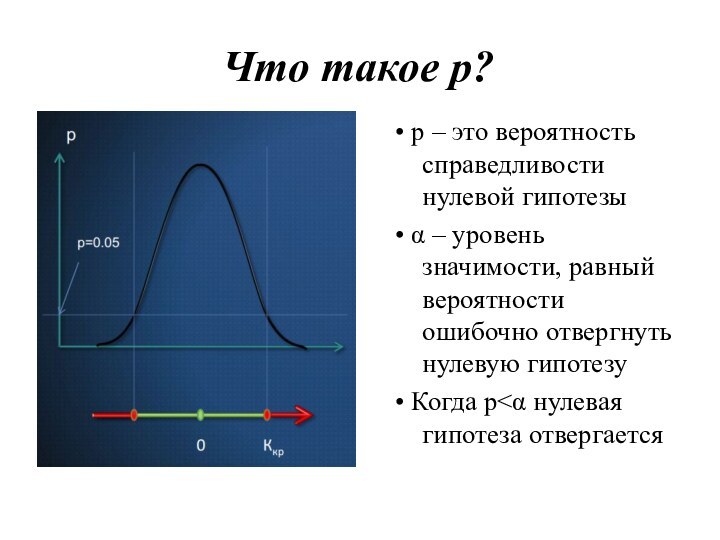
Что такое р?
• p – это вероятность справедливости
нулевой гипотезы
• α – уровень значимости, равный вероятности ошибочно
отвергнуть нулевую гипотезу
• Когда p<α нулевая гипотеза отвергается
Слайд 16
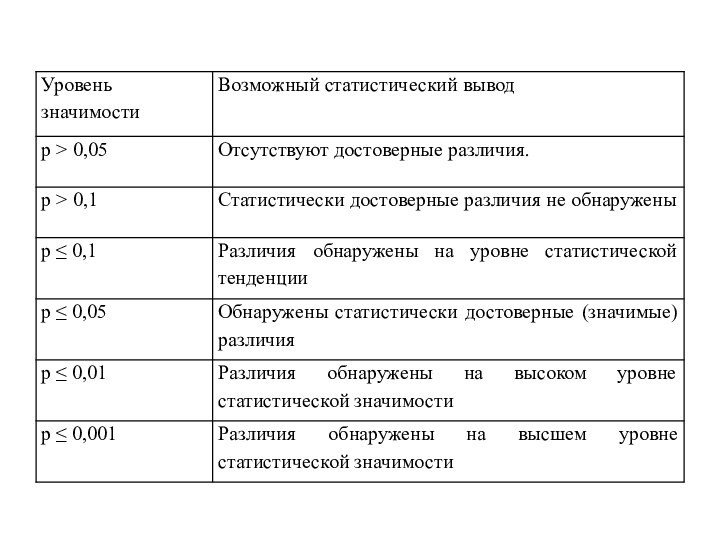
6. Уровень статистической значимости
(α -уровень) –
это количественно выраженная вероятность, свидетельствующая о том, что результаты
достоверны, вероятность ошибочного отклонения нулевой гипотезы. Более высокий α -уровень соответствует более низкому уровню доверия к найденной в выборке зависимости между переменными. Именно, α -уровень представляет собой вероятность ошибки, связанной с распространением наблюдаемого результата на всю популяцию.
Принято считать, что низшим уровнем статистической значимости является уровень α =0,05; достаточным – α =0,01; высшим – α =0,001.
