- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Урок одного уравнения
Содержание
- 2. Цели: рассмотреть различные методы решения тригонометрического
- 3. Уравнение одно
- 4. «Знание только тогда знание, когда оно приобретено
- 7. I способ Метод разложения на множители, используя
- 8. Произведение нескольких множителей равно 0 тогда и
- 9. Покажем на окружности x = π +
- 10. II способ Переход к однородному уравнению,
- 11. Произведение нескольких множителей равно 0 тогда
- 12. III способ При применении универсальной тригонометрической
- 13. Проверим, не произошло ли потери корней, это
- 14. IV способ Переход к простейшему тригонометрическому
- 15. Покажем решение на единичной окружности.
- 16. V способ Метод введения вспомогательного угла намного ускоряет процесс решения уравнения
- 18. Запишем в двух сериях sin(x – π/4)
- 19. Решим самостоятельно Решить каждое уравнение несколькими способами. (Работа в парах)
- 20. Сверим ответы.
- 21. Дома. Решить два уравнение (по выбору) всеми способами.
- 22. Спасибо за внимание
- 23. Скачать презентацию
- 24. Похожие презентации
Цели: рассмотреть различные методы решения тригонометрического уравнения;развивать умение логически мыслить.Оборудование:интерактивная доска. презентация, чертежные инструменты., тригонометрические формулы.






















Слайд 2
Цели: рассмотреть различные методы решения тригонометрического уравнения;
развивать
умение логически мыслить.
Слайд 3 Уравнение одно –
решений много.
Выполнили: Баранова Светлана
Езенкова Дарья
Руководитель: Секисова
Валентина Васильевна
МБОУ «СОШ №7»
г Касимов
Слайд 7 I способ Метод разложения на множители, используя формулы двойного
угла
sin x – cos x = 1Применим формулы двойного угла:
sin a = 2sin a/2cos a/2
cos a= 2cos² a/2 – 1
Тогда данное уравнение примет вид:
2sin x/2cos x/2 – (2cos² x/2 – 1) = 1
2sin x/2cos x/2 – 2cos² x/2 + 1 = 1
2sin x/2cos x/2 – 2cos² x/2 = 0
Разложим на множители
2cos x/2(sin x/2 – cos x/2) = 0
Слайд 8 Произведение нескольких множителей равно 0 тогда и только
тогда, когда хотя бы один из множителей равен 0,
а другие при этом определены.cos x/2 = 0 или sin x/2 – cos x/2 = 0
Частный случай. Имеем однородное
уравнение I степени, поделим на cos x/2 ≠ 0
x/2 = π/2 + πn, n ϵ Z tg x/2 – 1 = 0
x= π + 2πn, n ϵ Z tg x/2 = 1
x/2 = π/4 + πn, n ϵ Z
x = π/2 + 2 πn, n ϵ Z
Слайд 9
Покажем на окружности
x = π + 2πn,
n ϵ Z
x = π/2 + 2
πn, n ϵ ZОтвет: x= π + 2πn, n ϵ Z
x = π/2 + 2 πn, n ϵ Z
Слайд 10 II способ Переход к однородному уравнению, применяя основные тригонометрические
формулы
sin x – cos x = 1Решим уравнение, применим формулу двойного угла:
sin a = 2sin a/2 cos a/2
cos a = cos² a/2 – sin² a/2
1 = cos² a/2 + sin² a/2
2sin a/2cos a/2 - cos² a/2 + sin² a/2 = cos² a/2 + sin² a/2
2sin a/2cos a/2 - 2cos² a/2 = 0
Разложим на множители
2cos x/2(sin x/2- cos x/2) = 0
Слайд 11 Произведение нескольких множителей равно 0 тогда и
только тогда, когда хотя бы один из множителей равен
0, а другие при этом определены.cos x/2 = 0 или sin x/2 – cos x/2 = 0
Частный случай. Имеем однородное уравнение 1 степени, поделим
на cos x/2 ≠ 0
x/2 = π/2 + πn, n ϵ Z tg x/2 – 1 = 0
x= π + 2πn, n ϵ Z tg x/2 = 1
x/2 = π/4 + πn, n ϵ Z
x = π/2 + 2πn, n ϵ Z
Ответ: x= π + 2πn, n ϵ Z
x = π/2 + 2πn, n ϵ Z
Слайд 12 III способ При применении универсальной тригонометрической подстановки мы
можем любое тригонометрическое уравнение свести к алгебраическому, но при
этом необходимо помнить, что может произойти потеря корней. Поэтому необходимо выполнить проверку. sin x – cos x = 1
Применим универсальную подстановку
sin a = (2tg a/2)/(1+tg² x/2)
cos a = (1- tg² x/2)/(1+tg² x/2)
(2tg a/2)/(1+tg² x/2) - (1- tg² x/2)/(1+tg² x/2) = 1 (доп. множитель 1+tg² x/2 )
2tg x/2 – 1 + tg² x/2 = 1 + tg² x/2
2tg x/2 = 2
tg x/2 = 1
Частный случай. x/2 = π/4 + πn, n ϵ Z
x= π/2 + 2πn, n ϵ Z
Слайд 13 Проверим, не произошло ли потери корней, это те
значения, при которых tg x/2 не имеет смысла:
x/2 = π/2 + πn, n ϵ Z x= π + 2πn, n ϵ Z
Следовательно, корни x= π + 2πn потеряны.
2 sin π – cos π = 1
0 - (-1) = 1
1=1 верно
Ответ: x= π/2 + 2πn, n ϵ Z
x= π + 2πn, n ϵ Z
Слайд 14 IV способ Переход к простейшему тригонометрическому уравнению путем
применения формул сложения.
sin x – cos x = 1Применим формулы привидения
cos a = sin(π/2 – a), тогда
sin x – sin(π/2 – x) = 1
Применим формулу разности синусов:
sin x – sin b = 2cos(a+b)/2sin(a-b)/2
2sin(x – π/2 + x)/2cos(x + π/2 – x)/2 =1
2sin(2x – π/2)cos π/4 =1
2sin(x – π/4)√2/2 = 1
√2sin(x – π/4) = 1
sin(x – π/4) = √2/2
Получили простейшее тригонометрическое уравнение.
x - π/4 = (-1)^narcsin √2/2 + πn, n ϵ Z
x - π/4 = (-1)^nπ/4 + πn, n ϵ Z
x = (-1)^nπ/4 + π/4 + πn, n ϵ Z
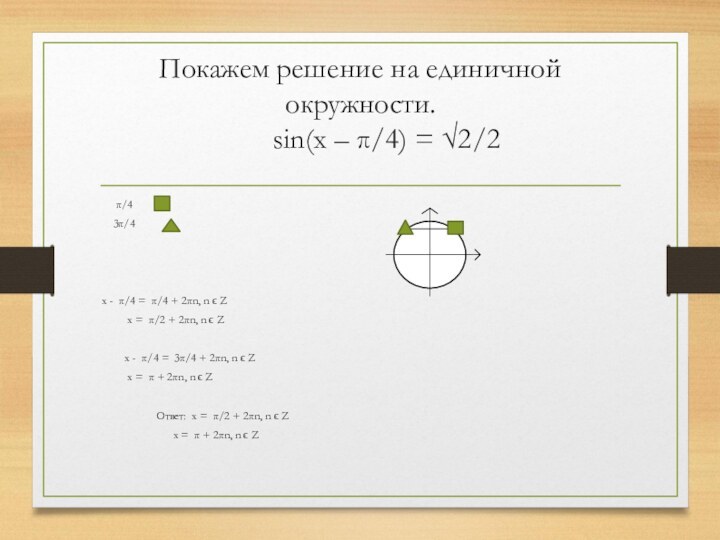
Слайд 15 Покажем решение на единичной окружности.
sin(x – π/4) = √2/2
π/4
3π/4x - π/4 = π/4 + 2πn, n ϵ Z
x = π/2 + 2πn, n ϵ Z
x - π/4 = 3π/4 + 2πn, n ϵ Z
x = π + 2πn, n ϵ Z
Ответ: x = π/2 + 2πn, n ϵ Z
x = π + 2πn, n ϵ Z
Слайд 18
Запишем в двух сериях
sin(x – π/4) =
√2/2
Корни I серии обозначим - π/4
Корни
II серии обозначим - 3π/4x – π/4 = π/4 + 2πn, n ϵ Z
x = π/2 + 2πn, n ϵ Z
x – π/4 = 3π/4 + 2πn, n ϵ Z
x= π + 2πn, n ϵ Z
Ответ: x = π/2 + 2πn, n ϵ Z
x= π + 2πn, n ϵ Z