- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Отчёт по самообразованию Активизация познавательного интереса на уроках математики учебно-методический материал по математике
Содержание
- 2. « Предмет математики настолько
- 3. Актуальность: Приоритетом современного образования, гарантирующим его
- 4. Цель работы по данной теме - применение
- 5. Задачи Эффективная и быстрая адаптация школьников к
- 6. Познавательный интерес - это один из важнейших
- 7. Удивление – сильный стимул познанияУченики испытывают удивление
- 8. Доказано, что дети запоминают 10% того, что
- 9. По характеру познавательной деятельности игры можно разделить
- 10. 2. Игры, требующие воспроизводящей деятельности. К этой группе
- 11. 3. Игры, в которых запрограммирована преобразующая (контролирующая) деятельность
- 12. 4. Игры, в которые включены элементы поисковой деятельности,
- 13. Провоцирующие задачи обладают высоким развивающим потенциалом. Они
- 14. Можно выделить следующие разновидности задач провоцирующего характера:
- 15. -Задачи, условия которых тем или иным способом
- 16. -Задачи, вынуждающие придумывать, строить такие математические объекты,
- 17. Задачи, вводящие в заблуждение из-за неоднозначности трактовки
- 18. Задачи, условия которых допускают возможность «опровержения» семантически
- 19. Задания, направленные на развитие внимания. 1. Отыскание
- 20. Задания, направленные на развитие внимания.Найди 10 отличий.Найди на чертеже 11 треугольников.
- 21. Задания, направленные на развитие восприятия и воображения.
- 22. Задания, направленные на развитие логического мышления. Задачи
- 23. Комбинаторная задачаУчащимся предлагается следующая проблема: « У
- 24. Числовые фигуры Задание: Сумма цифр человечка-его возраст. Узнай возраст
- 25. Математический фокусЗадумайте число, прибавьте к нему 14,
- 26. Задания, направленные на развитие памяти. Запомни двузначные
- 27. Рисуем по памяти узоры
- 28. Проблемное обучение Решить удобным способом
- 29. РЕЗУЛЬТАТЫ: домашнюю работу по предмету с
- 30. Участие в конкурсах:Международный математический конкурс-игра «Кенгуру» Мерзлов Дмитрий - I место по школе.
- 31. Мудр был человек, связавший слово «урок» со
- 32. Скачать презентацию
- 33. Похожие презентации
« Предмет математики настолько серьёзен, что надо не упускать случая сделать его занимательным»






























Слайд 3 Актуальность: Приоритетом современного образования, гарантирующим его высокое качество
и результативность, должно стать обучение, ориентированное на самосовершенствование и
самореализацию личности. Поэтому на смену модели "образование-преподавание" пришло "образование-взаимодействие", когда личность ученика становится центром внимания педагога. Помочь учащимся в полной мере проявить свои способности, развить инициативу, самостоятельность, творческий потенциал – одна из основных задач современной школы. А успешная реализация этой задачи во многом зависит от сформированности у учащихся познавательных интересов. Именно это, на мой взгляд, и определяет активность школьника в познании себя и окружающего мира.Слайд 4 Цель работы по данной теме - применение целостной
системы методов, приемов обучения в сочетании традиционных и нетрадиционных
форм работы, ориентированных на развитие основных характеристик мышления, на повышение уровня самостоятельной практической и умственной деятельности детей, на развитие навыков самоконтроля.
Слайд 5
Задачи
Эффективная и быстрая адаптация школьников к учебной
деятельности.
Повышение интереса к предмету «Математика».
Развитие основных познавательных
процессов (внимания, памяти, мышления, воображения, восприятия). Развитие инициативы, самостоятельности, творческого потенциала.
Включение учащихся в поисковую деятельность по предмету.
Развитие младшего школьника как субъекта собственной деятельности и поведения, его эффективную социализацию.
Слайд 6 Познавательный интерес - это один из важнейших мотивов
учения школьников. Активизация познавательной
деятельности ученика без развития его познавательного интереса не только трудна, но практически и невозможна. Вот почему в процессе обучения необходимо систематически возбуждать, развивать и укреплять познавательный интерес учащихся и как важный мотив учения, и как стойкую черту личности, и как мощное средство воспитывающего обучения, повышения его качества.
Слайд 7
Удивление – сильный стимул познания
Ученики испытывают удивление когда,
составляя задачу, узнают, что одна сова за год уничтожает
тысячу мышей, которые за год способны истребить тонну зерна, и что сова, живя в среднем 50 лет, сохраняет нам 50 тонн хлеба.Слайд 8 Доказано, что дети запоминают 10% того, что читают,
26% того, что слышат, 30% того, что видят, 50%
того, что видят и слышат, 70% того, что обсуждают с другими, 80% того, что основано на личном опыте, 90% того, что проговаривают в то время, когда делают, 95% того, чему они обучаются сами. Данная информация позволяет сделать вывод. Результат обучения зависит от степени активности учащихся в учебном процессе.Слайд 9 По характеру познавательной деятельности игры можно разделить на
следующие группы:
Игры, требующие от детей исполнительной деятельности. С помощью
этих игр дети выполняют действия по образцу. («Составим узор» )Слайд 10 2. Игры, требующие воспроизводящей деятельности. К этой группе относятся
игры, направленные на формирование вычислительных навыков.(«Лучший лётчик», «Математическая рыбалка»,
«Помоги собрать бананы»)Слайд 11 3. Игры, в которых запрограммирована преобразующая (контролирующая) деятельность детей.
С помощью этих игр дети изменяют примеры и задачи
в другие, логически связанные с ними. («Составь круговые примеры», «Математическая эстафета»)Слайд 12 4. Игры, в которые включены элементы поисковой деятельности, где
целью игры является формулирование учащимися по рисунку, схеме и
опорным словам математического правила. («Угадайка», «Определи курс движения самолёта»)Слайд 13 Провоцирующие задачи обладают высоким развивающим потенциалом. Они способствуют
воспитанию одного из важнейших качеств мышления – критичности, приучают
к анализу воспринимаемой информации, её разносторонней оценке, повышают познавательный интерес.Слайд 14 Можно выделить следующие разновидности задач провоцирующего характера: -Задачи, условия
которых в той или иной форме навязывают неверный ответ.
-
Сколько прямоугольников можно насчитать в изображении окна? - Сколько знаков будет в числе, в записи которого 5 нулей?
- Какое из чисел 333, 555, 666, 999 не делится на 3?
Слайд 15 -Задачи, условия которых тем или иным способом подсказывают
неверный путь решения.
- Тройка лошадей проскакала 15км. Сколько км
проскакала каждая лошадь?- Крышка имеет 4 угла. Если один из них отпилить, сколько углов будет у крышки?
- 6 рыбаков съедят 6 судаков за 6 дней. Сколько судаков съедят 12 рыбаков за 12 дней?
Слайд 16 -Задачи, вынуждающие придумывать, строить такие математические объекты, которые
при заданных условиях не могут иметь места.
- Используя цифры
1 и 4, запишите трёхзначное число, дающее при делении на 3 остаток равный 2.Придумать такое число невозможно, поскольку любое число, удовлетворяющее условию задачи, делится на 3 без остатка.
Слайд 17 Задачи, вводящие в заблуждение из-за неоднозначности трактовки терминов,
словесных оборотов, буквенных или числовых выражений
- На листе бумаги
записано число 606. Какое действие нужно совершить, чтобы увеличить его в полтора раза? Здесь имеется в виду не математическое действие, а просто игра с листом: его нужно перевернуть и получится 909.Слайд 18 Задачи, условия которых допускают возможность «опровержения» семантически верного
решения синтаксическим или иным нематематическим решением.
- 3 спички выложены
на столе так, что получилось 4. могло ли такое быть, если других предметов на столе не было?Отрицательный ответ опровергается : IV.
Слайд 19
Задания, направленные на развитие внимания.
1. Отыскание ходов
в обычных и числовых лабиринтах.
2. Пересчёт предметов, изображенных неоднократно
пересекающимися контурами.3. Отыскание чисел по таблицам Шульте.
4. Найди сходство и различие.
Слайд 20
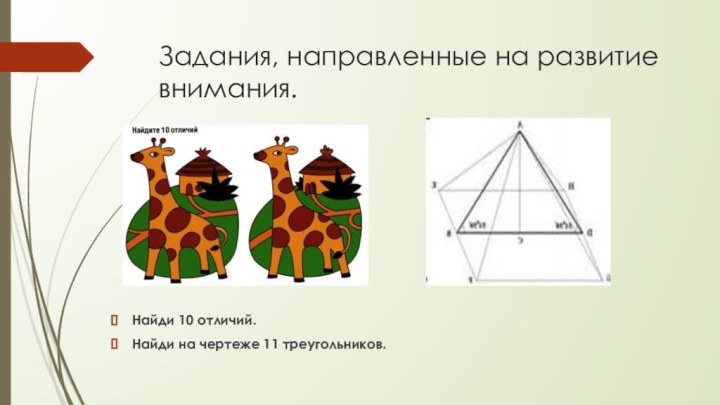
Задания, направленные на развитие внимания.
Найди 10 отличий.
Найди на
чертеже 11 треугольников.
Слайд 21
Задания, направленные на развитие восприятия и воображения.
Подбери заплатку
к сапожку.
Собери разбитую тарелку, кувшин, вазу.
Упражнение «Геометрические фигуры».
Слайд 22
Задания, направленные на развитие логического мышления.
Задачи в стихотворной
форме.
Задачи шутки.
Магические квадраты.
Числовые фигуры.
Задачи на смекалку.
Задачи с геометрическим
содержанием.Кроссворды и ребусы.
Комбинаторные задачи.
Математические фокусы.
Слайд 23
Комбинаторная задача
Учащимся предлагается следующая проблема: « У тебя
60 рублей. Родители отпустили тебя в парк покататься на
каруселях.Предлагаются следующие расценки.
-Вход в парк – 5 рублей
-«Колесо обозрения» – 10 рублей
-«Сюрприз – 35 рублей.
-«Американские горки» – 45 рублей
«Комната смеха» – 25 рублей
Какой выбор ты сделаешь, если ни один из аттракционов нельзя посетить дважды?
Слайд 25
Математический фокус
Задумайте число, прибавьте к нему 14, к
результату прибавьте 6, вычтите задуманное число. У вас получилось
20.Формула для разгадывания фокуса: а + 14 + 6 – а = 20
Слайд 26
Задания, направленные на развитие памяти.
Запомни двузначные числа.
Запомни математические
термины.
Цепочка слов.
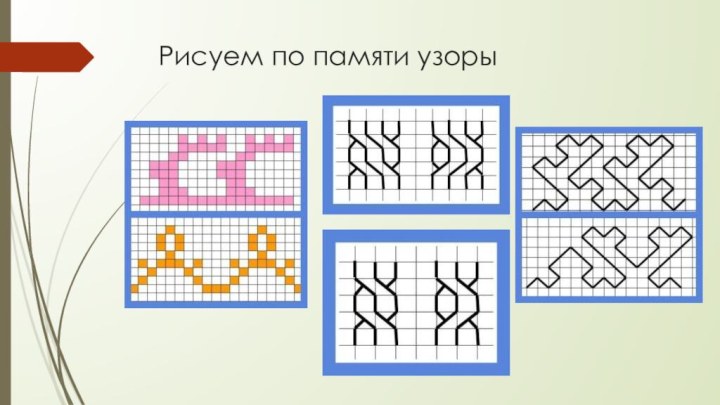
Рисуем по памяти узоры.
Запомни и воспроизведи рисунки.
Зрительные диктанты.
Слуховые
диктанты.Слайд 28 Проблемное обучение Решить удобным способом (40+10) -
7 (60+10) – 4 Вставить числа в окошки по данному
образцу 40 = 30 + 10 80 = … + 10 60 = 50 + 10 50 = … + … Опорные схемыТир
?
Кух.
5
13





























