- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Парабола
Содержание
- 2. ПонятиеПараболой называется множество таких точек плоскости, для
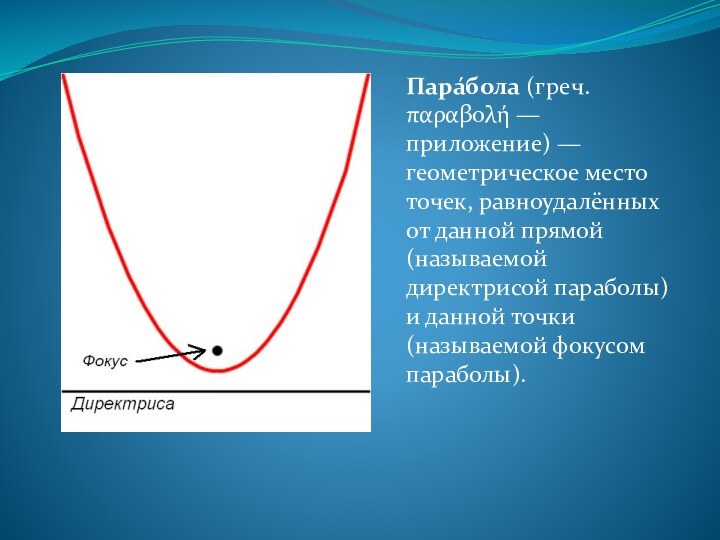
- 3. Пара́бола (греч. παραβολή — приложение) — геометрическое место точек,
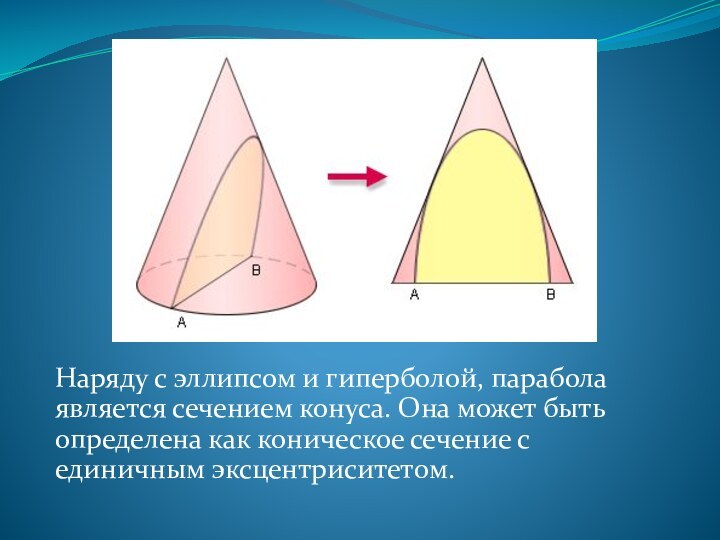
- 4. Наряду с эллипсом и гиперболой, парабола является
- 6. УравненияКаноническое уравнение параболы в прямоугольной системе координат:
- 7. Квадратное уравнение y = ax2 +
- 8. ПостроениеПараболу можно построить «по точкам» с помощью
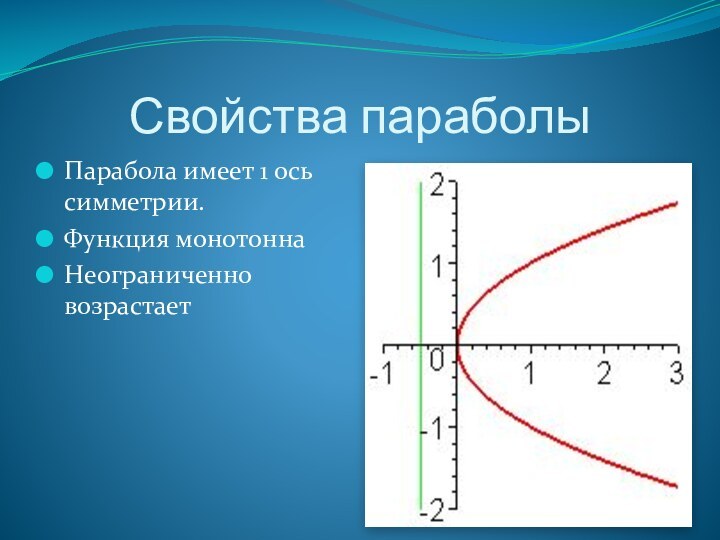
- 9. Свойства параболыПарабола имеет 1 ось симметрии.Функция монотонна Неограниченно возрастает
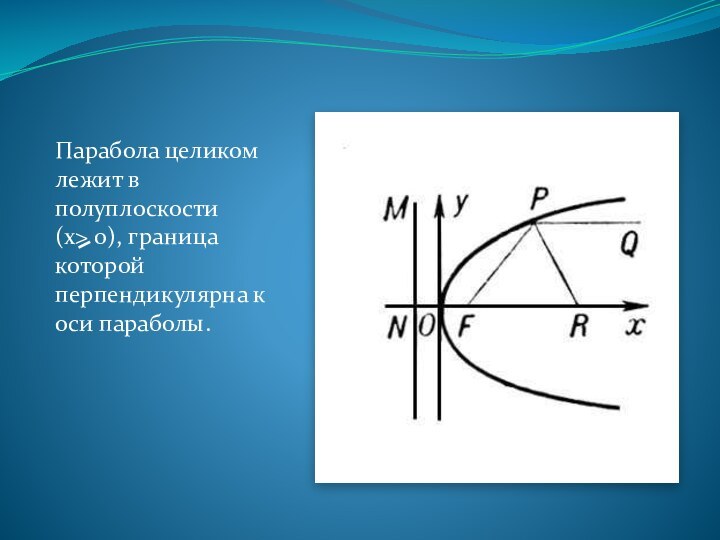
- 10. Парабола целиком лежит в полуплоскости (x> 0), граница которой перпендикулярна к оси параболы.
- 11. Парабола вокруг нас
- 18. Скачать презентацию
- 19. Похожие презентации
ПонятиеПараболой называется множество таких точек плоскости, для которых расстояние до фиксированной точки равно расстоянию до фиксированной прямой, не проходящей через эту точку.