Слайд 2
Содержание
Понятие вектора в пространстве.
Понятие вектора
Равенство векторов
Сложение и вычитание
векторов. Умножение вектора на число.
Сложение и вычитание векторов
Сумма нескольких
векторов
Умножение вектора на число
Компланарные векторы
Компланарные векторы
Разложение вектора по трем некомпланарным векторам
Координаты точки и координаты вектора.
Прямоугольная система координат в пространстве
Координаты вектора
Связь между координатами векторов и координатами точек
Простейшие задачи в координатах
Скалярное произведение векторов
Скалярное произведение векторов
Вычисление углов между прямыми и плоскостями
Список использованной литературы
Слайд 3
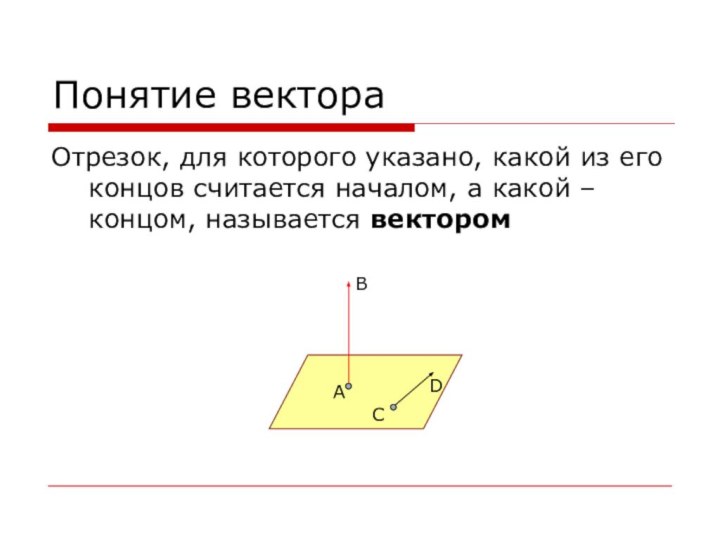
Понятие вектора
Отрезок, для которого указано, какой из его
концов считается началом, а какой – концом, называется вектором
A
B
C
D
Слайд 4
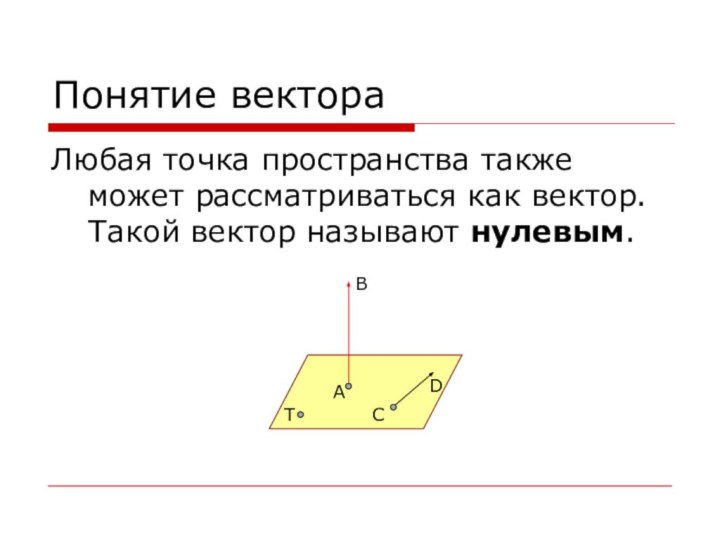
Понятие вектора
Любая точка пространства также может рассматриваться как
вектор. Такой вектор называют нулевым.
A
B
C
D
T
Слайд 5
Понятие вектора
Длиной ненулевого вектора AB называется длина отрезка
AB.
Длина вектора AB обозначается так:
Слайд 6
Понятие вектора
Два ненулевых вектора называются коллинеарными, если они
лежат на одной прямой или на параллельных прямых.
Если векторы
коллинеарные и при этом их лучи совпадают, то такие векторы называют сонаправлеными, а если не совпадают – противоположно направленными.
Слайд 7
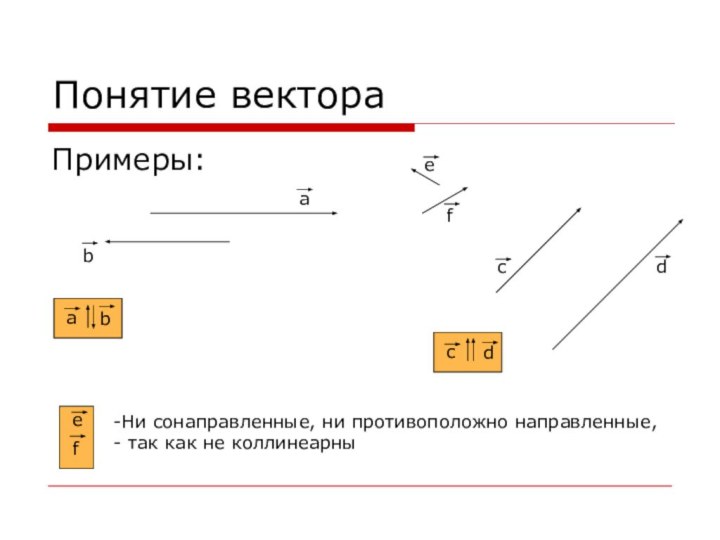
Понятие вектора
Примеры:
Ни сонаправленные, ни противоположно направленные,
так как
не коллинеарны
Слайд 8
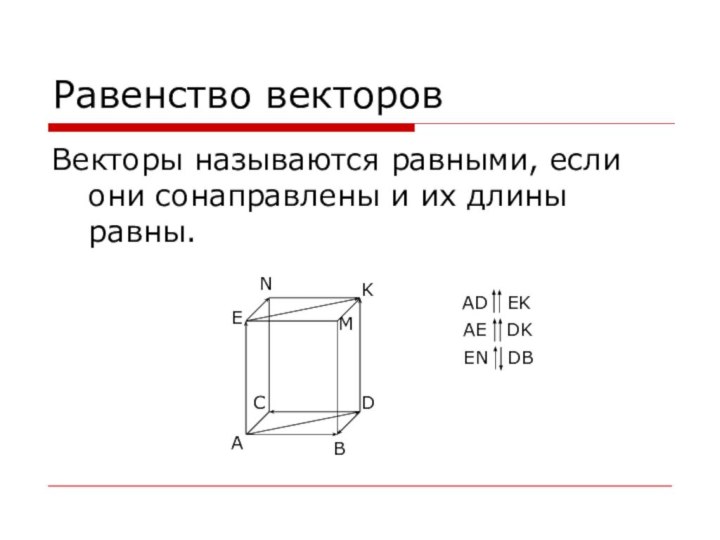
Равенство векторов
Векторы называются равными, если они сонаправлены и
их длины равны.
A
B
C
D
E
N
K
M
AD EK
AE DK
EN DB
Слайд 9
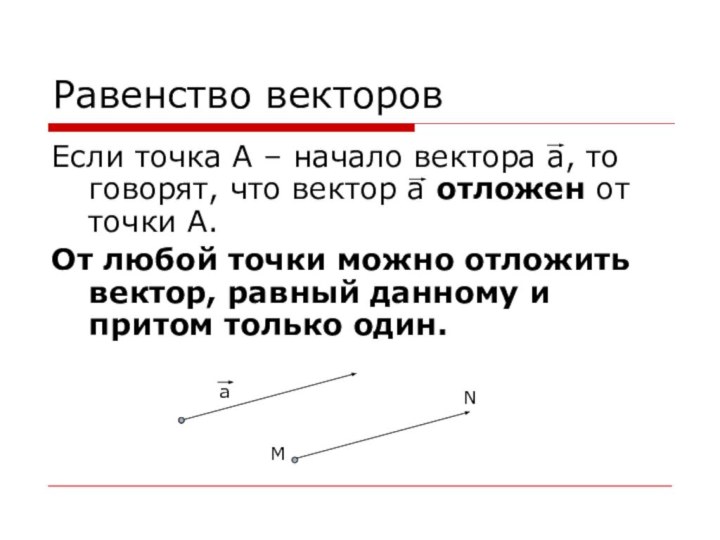
Равенство векторов
Если точка А – начало вектора а,
то говорят, что вектор а отложен от точки А.
От
любой точки можно отложить вектор, равный данному и притом только один.
M
N
Слайд 10
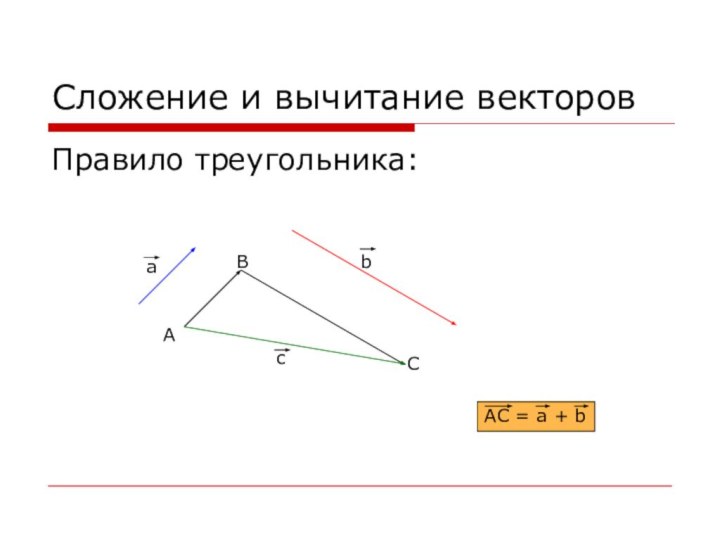
Сложение и вычитание векторов
Правило треугольника:
А
B
C
Слайд 11
Сложение и вычитание векторов
+
+
Слайд 12
Сложение и вычитание векторов
Для любых векторов a, b
и c справедливы равенства:
a+b=b+a
(a+b)+c=a+(b+c)
Слайд 13
Сложение и вычитание векторов
Разностью векторов a и b
называется такой вектор, сумма которого с вектором b равна
вектору a.
Иными словами: a-b=a+(-b)
-
Слайд 14
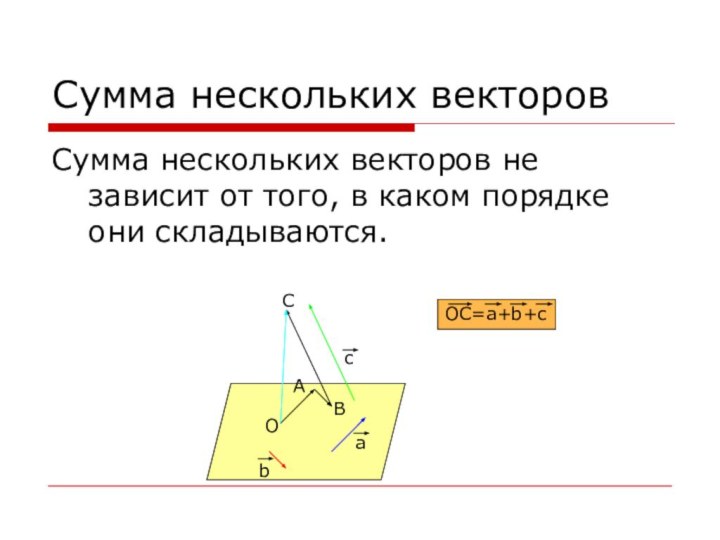
Сумма нескольких векторов
Сумма нескольких векторов не зависит от
того, в каком порядке они складываются.
А
B
C
О
Слайд 15
Умножение вектора на число
Произведением ненулевого вектора а на
число k называется такой вектор b, длина которого равна
|k| * |a|, причем векторы a и b сонаправлены при k ≥ 0 и противоположно направлены при k < 0.
Произведением нулевого вектора на любое число считается нулевой вектор
Слайд 16
Умножение вектора на число
Для любых векторов a, b
и любых чисел k, l справедливы равенства:
(kl)a=k(la)
k(a+b)=ka+kb
(k+l)a=ka+la
Слайд 17
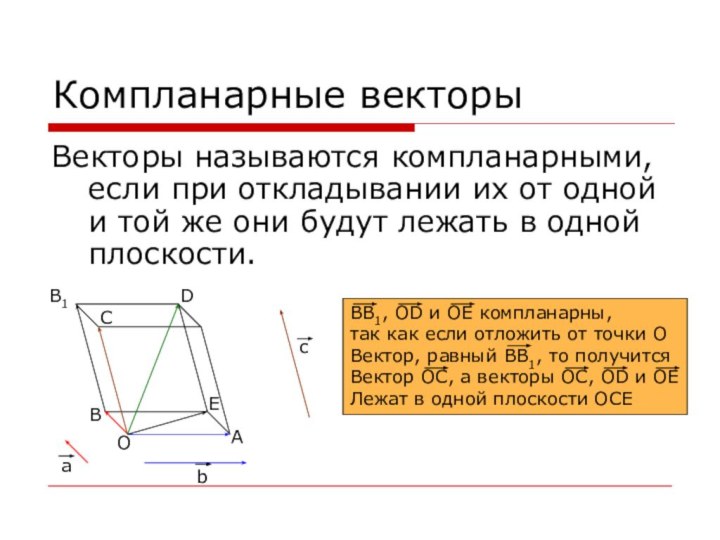
Компланарные векторы
Векторы называются компланарными, если при откладывании их
от одной и той же они будут лежать в
одной плоскости.
O
A
B
B1
E
C
D
Слайд 18
Компланарные векторы
Если вектор с можно разложить по векторам
a и b, т.е. представить в виде:
c=xa+yb
Где x и
у – некоторые числа, то векторы a, b и с компланарны.
O
A
A1
B
B1
C
Слайд 19
Разложение вектора по трем некомпланарным векторам
Теорема:
Любой вектор можно
разложить по трем некомпланарным векторам, причем коэффициенты разложения определяются
единственным образом.
Слайд 20
Разложение вектора по трем некомпланарным векторам
Доказательство:
Дано:
a, b
и с – некомпланарные векторы, ОА=a, OB=b, OC=c, OP=p
O
A
B
C
P
P2
P1
2)
Векторы коллинеарны, поэтому можно записать так:
OP=x*OA + y*OB + z*OC
3) Допустим, что вектор можно разложить
еще по трем числам: x1,y1,z1. Тогда,
используя свойство действий над векторами,
получим:
Слайд 21
Разложение вектора по трем некомпланарным векторам
Это равенство выполняется
только тогда, когда x-x1=0, y-y1=0, z-z1=0.
Отсюда следует:
5)
Из этой
формулы следует, что векторы a, b и с компланарны. Но это противоречит условию теоремы. Значит x=x1, y=y1 и z=z1.
Теорема доказана.
Слайд 22
Координаты точки и координаты вектора
Если через точку пространства
проведены три попарно перпендикулярные прямые,
На каждой из них выбрано
направление и выбрана единица измерения, то говорят, что задана
прямоугольная система координат
O
Слайд 23
Координаты точки и координаты вектора
Прямые с выбранными на
них направлениями называют осями координат.
А их общая точка –
началом координат
O
x
y
z
Слайд 24
Координаты точки и координаты вектора
Точка О разделяет каждую
из осей координат на два луча. Луч, направление которого
совпадает с направлением оси, называется положительной полуосью, а другой луч – отрицательной полуосью.
O
Отрицательная Положительная
x
y
z
Слайд 25
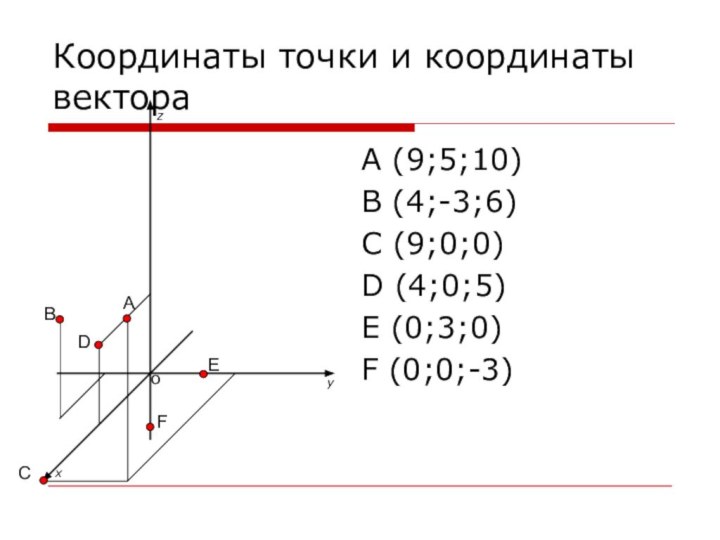
Координаты точки и координаты вектора
A (9;5;10)
B (4;-3;6)
C (9;0;0)
D
(4;0;5)
E (0;3;0)
F (0;0;-3)
o
A
B
C
D
E
F
x
y
z
Слайд 26
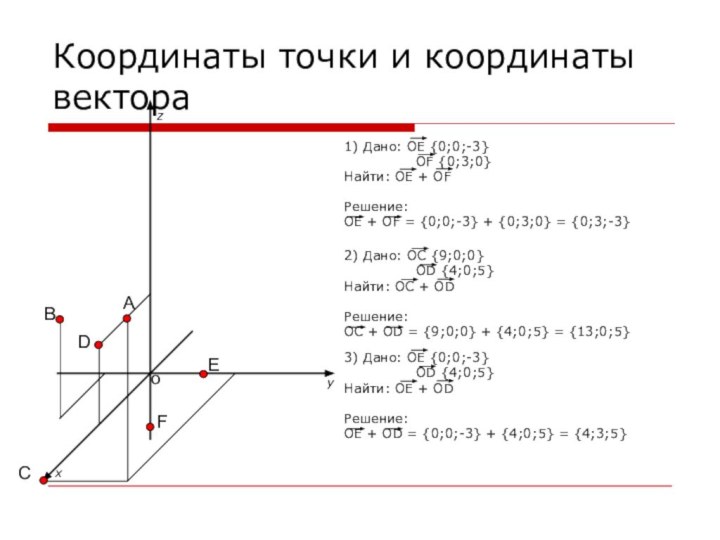
Координаты точки и координаты вектора
1) Дано: OE {0;0;-3}
OF
{0;3;0}
Найти: OE + OF
Решение:
OE + OF = {0;0;-3}
+ {0;3;0} = {0;3;-3}
o
A
B
D
E
F
C
x
y
z
Слайд 27
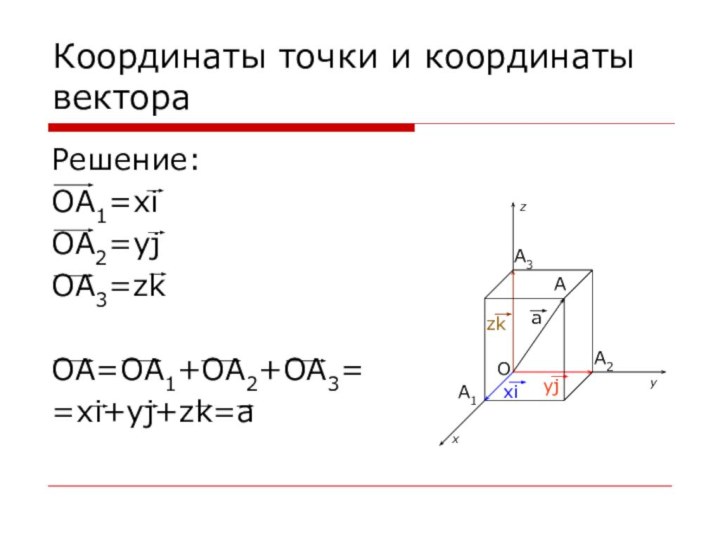
Координаты точки и координаты вектора
Любой вектор можно разложить
по координатным векторам, т.е. представить в виде
a=xi+yj+zk
Причем коэффициенты разложения
x, y, z определяются единственным образом
O
x
y
z
Слайд 28
Координаты точки и координаты вектора
10 Каждая координата суммы
двух или более векторов равна сумме соответствующий координат этих
векторов.
20 Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.
30 Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.
Слайд 29
Координаты точки и координаты вектора
Дано: a{1;-2;0}, b{0;3;-6}, c{-2;3;1}
Найти:
Решение:
по правилу 30: 2a{2;-4;0}, b{0;-1;2}
По правилу 10
можно вычислить координаты вектора p.
Слайд 30
Координаты точки и координаты вектора
Вектор, конец которого совпадает
с данной точкой, а начало – с началом координат,
называется радиус-вектором данной точки.
Докажем, что координаты любой точки равны соответствующим координатам её радиус-вектора.
Слайд 31
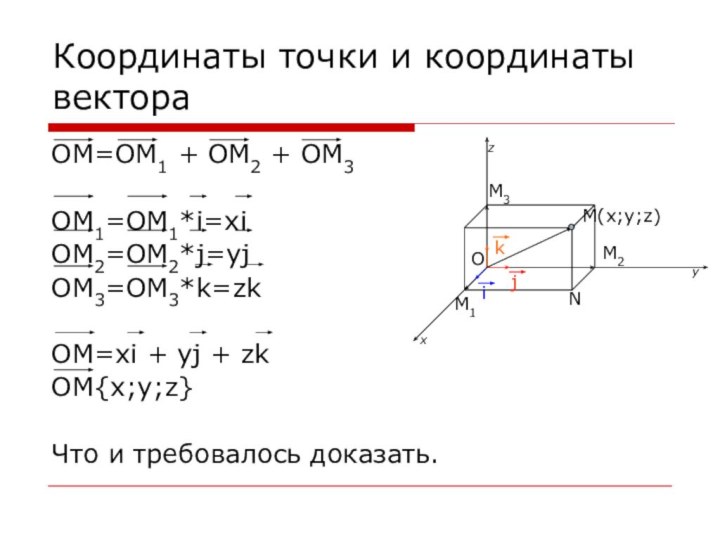
Координаты точки и координаты вектора
OM=OM1 + OM2 +
OM3
OM1=OM1*i=xi
OM2=OM2*j=yj
OM3=OM3*k=zk
OM=xi + yj + zk
OM{x;y;z}
Что и требовалось доказать.
O
x
y
z
N
M(x;y;z)
M1
M2
M3
Слайд 32
Координаты точки и координаты вектора
Каждая координата вектора равна
разности соответствующих координат его конца и начала.
Слайд 33
Координаты точки и координаты вектора
Координаты середины отрезка:
Дано: A(x1;y1;z1),
B(x2;y2;z2), C(x;y;z)
C-середина AB. Найти координаты С.
Решение:
OC=(OA+OB)/2
x=(x1+x2)/2
y=(y1+y2)/2
z=(z1+z2)/2
x
y
z
A (x1;y1;z1)
B
(x2;y2;z2)
C (x;y;z)
O
Слайд 34
Координаты точки и координаты вектора
Каждая координата середины отрезка
равна полусумме соответствующих координат его концов
Слайд 35
Координаты точки и координаты вектора
Вычисление длины вектора по
его координатам.
Дано: а{x;y;z}. Доказать:
x
y
z
O
A1
A2
A3
A
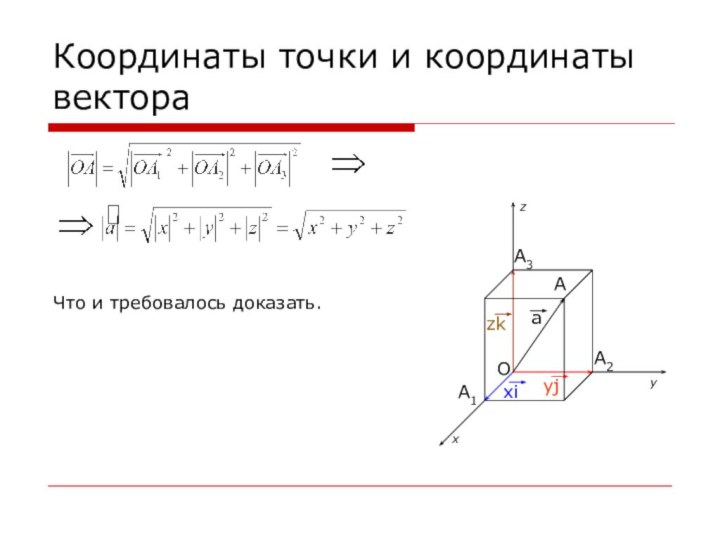
Слайд 36
Координаты точки и координаты вектора
Решение:
OA1=xi
OA2=yj
OA3=zk
OA=OA1+OA2+OA3=
=xi+yj+zk=a
x
y
z
O
A1
A2
A3
A
Слайд 37
Координаты точки и координаты вектора
x
y
z
O
A1
A2
A3
A
Что и требовалось доказать.
Слайд 38
Координаты точки и координаты вектора
Расстояние между двумя точками.
Дано:
М1(x1;y1;z1), M2(x2;y2;z2)
Решение:
Таким образом:
Слайд 39
Скалярное произведение векторов
Скалярным произведением двух векторов называется произведение
их длин на косинус угла между ними.
Слайд 40
Скалярное произведение векторов
Скалярное произведение ненулевых векторов равно нулю
тогда и только тогда, когда эти векторы перпендикулярны
Слайд 41
Скалярное произведение векторов
Скалярный квадрат вектора (т.е. скалярное произведение
вектора на себя) равен квадрату его длины.
Слайд 42
Скалярное произведение векторов
Косинус угла α между ненулевыми векторами
вычисляется по формуле:
Слайд 43
Скалярное произведение векторов
Для любых векторов a, b и
с и любого числа k справедливы равенства:
10 a2 ≥
0, причем a2 > 0 при a ≠ 0
20 ab=ba
30 (a+b)c=ac+bc
40 k(ab)=(ka)b