- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС (9 КЛАСС)
Содержание
- 2. Этот урок - урок Добра, Мудрости, Радости
- 3. Урок геометрии в 9 классеТема урока: "Параллельный перенос"
- 4. Обучающая: Закрепить знания
- 5. Развивающая:Развивать логическое мышление,
- 6. Воспитывающая:Формирование умения работать
- 7. Валеологическая:Создание оптимальных условий учебного процесса. Рациональное чередование разных видов деятельности.Цели урока:
- 8. План урока1. Организационный момент.2. Задание на дом.3.
- 9. Задание на домп.116,вопросы 14,
- 10. Проверка домашнего задания
- 11. Отображение плоскости на себя. Выполняются следующие условия:Каждой
- 12. Движение – отображение плоскости на себя, сохраняющее
- 13. А1АlПреобразование, при котором каждая точка А фигуры
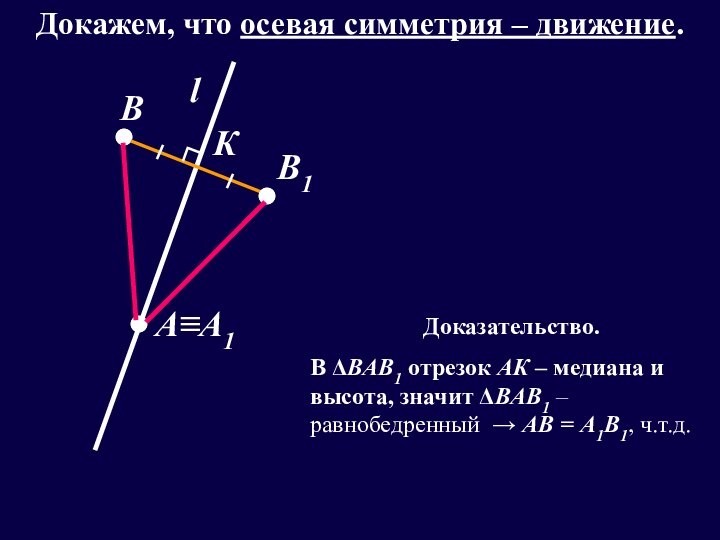
- 14. lА≡А1ВВ1КДокажем, что осевая симметрия – движение.Доказательство.В ΔВАВ1
- 15. В частности, если при осевой симметрии относительно
- 16. Преобразование, переводящее каждую точку А фигуры в
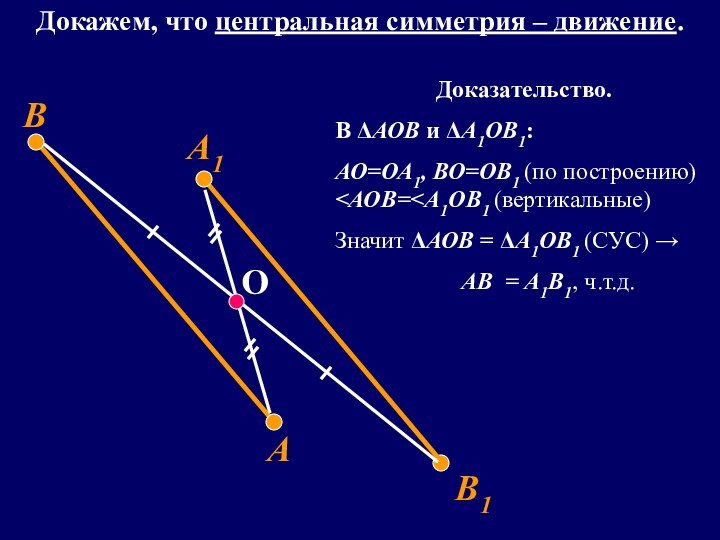
- 17. А1В1ОАВДокажем, что центральная симметрия – движение.Доказательство.В ΔАОВ и ΔА1ОВ1:АО=ОА1, ВО=ОВ1 (по построению)
- 18. Если при центральной симметрии относительно центра О
- 19. Осевую симметрию исторически называют геральдической
- 20. После падения Византии племянница ее последнего императора
- 21. а
- 22. Симметрия вокруг нас Симметричны снежинки, кристаллы, листья, цветы. Симметричны животные, рыбы, птицы, насекомые.Симметрично человеческое тело.
- 26. Любая жизнь подобна бесценному алмазуСПАСАЯ ПРИРОДУ – ТЫ СПАСАЕШЬ СЕБЯ
- 27. Нагляднее всего симметрия видна в архитектуре.
- 30. Мы увидели симметрию вокруг нас
- 31. Математический
- 32. 2. Начертите прямую а и точку В
- 33. 3. Закончите предложение: «Преобразование фигуры F в фигуру F1 называется движением, если оно ...».
- 34. 4. Треугольники АВС и МКР симметричны
- 35. 5. Два ромба симметричны друг другу относительно
- 36. 6. В какую фигуру переходит при движении отрезок длиной в 9 см?
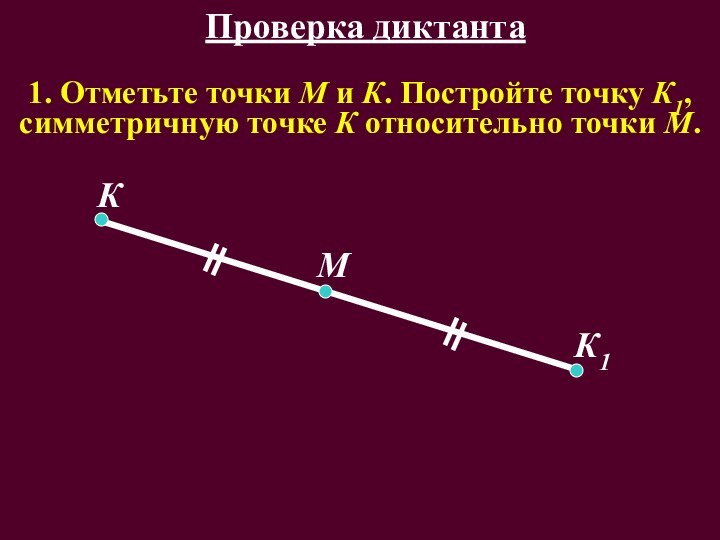
- 37. 1. Отметьте точки М и К. Постройте точку К1, симметричную точке К относительно точки М.КК1МПроверка диктанта
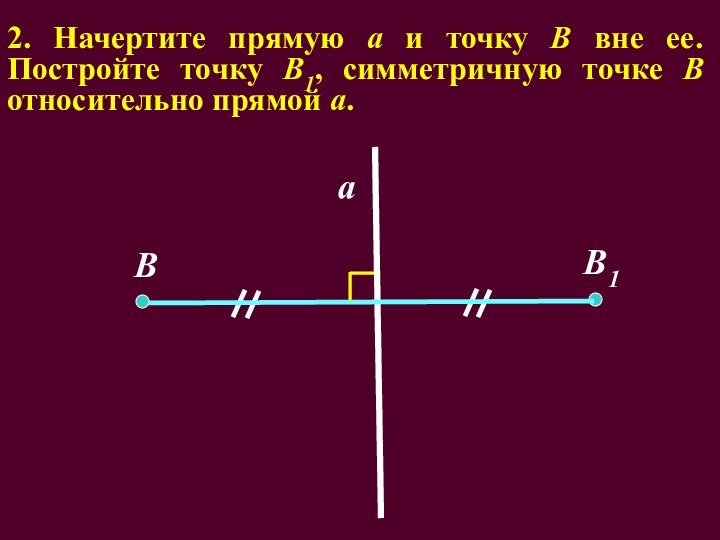
- 38. 2. Начертите прямую а и точку В
- 39. 3. Закончите предложение: «Преобразование фигуры F в
- 40. 4. Треугольники АВС и МКР симметричны относительно
- 41. 5. Два ромба симметричны друг другу относительно
- 42. 6. В какую фигуру переходит при движении
- 43. Параллельные прямыеаba ׀׀ b
- 44. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольникВАDСАВ=СD, АВ׀׀СD → АВСD-параллелограммпараллелограмм
- 45. ПараллелограммВАDС
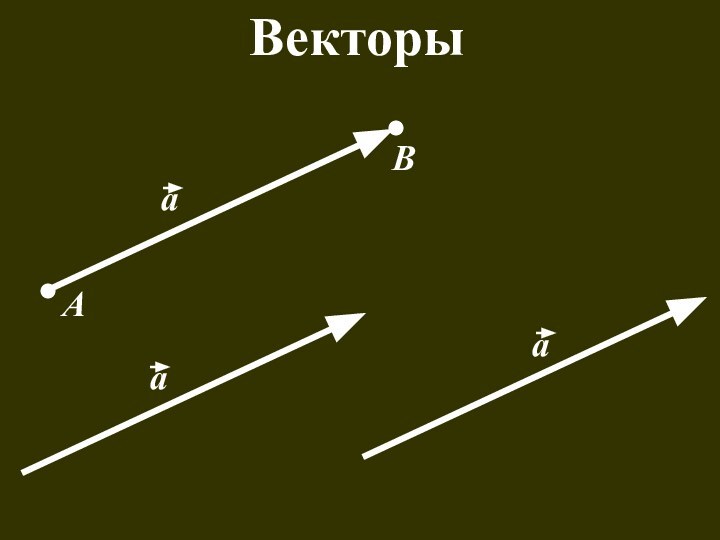
- 46. ВекторыаааАВ
- 47. Преобразование, при котором каждая точка фигуры перемещается
- 48. Чтобы задать параллельный перенос
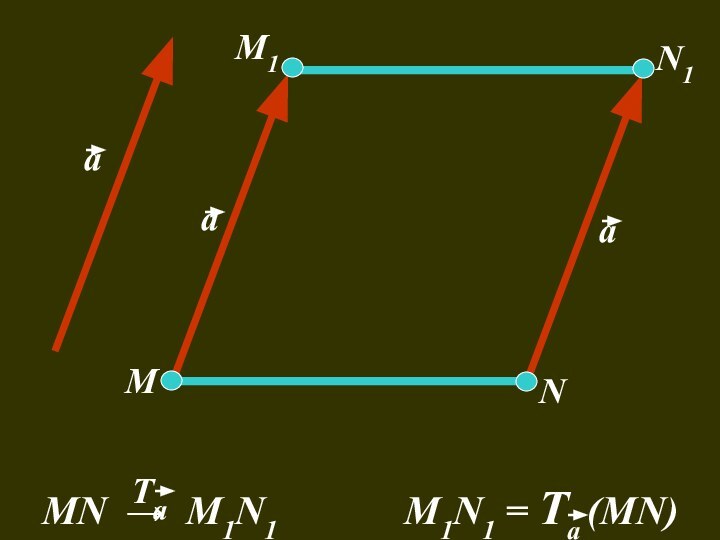
- 49. аааММ1N1NMN → M1N1
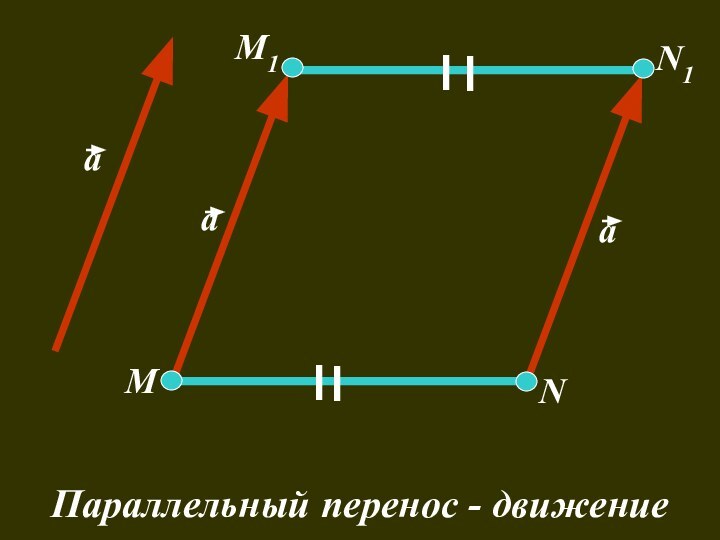
- 50. аааММ1N1NПараллельный перенос - движение
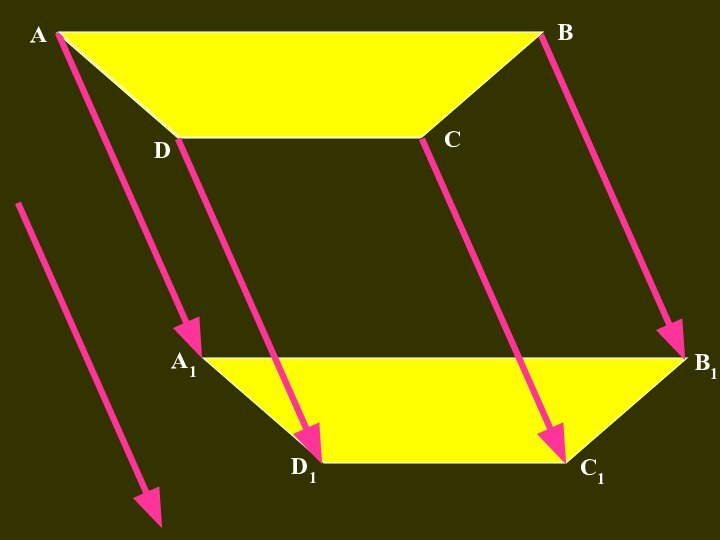
- 51. АА1DСВВ1С1D1
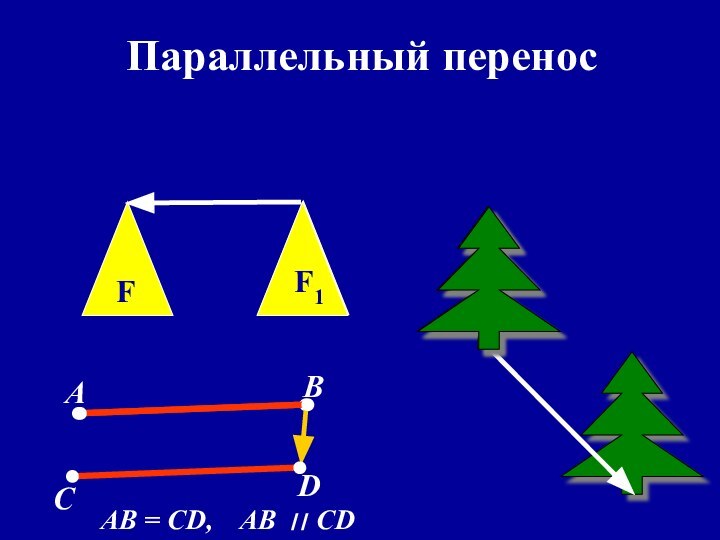
- 52. Параллельный переносАВСDAB = CD,AB ׀׀ CD FF1F1
- 53. Для параллельного переноса имеют место следующие свойства:
- 54. Решим на закрепление:№1162,№1163(а)№1164.
- 55. Решим на закрепление: Построить образы отрезка, треугольника и четырехугольника при параллельном переносе.
- 56. Разноуровневая практическая работаАСВ Начертите отрезок АВ и
- 57. Преобразование, при котором каждая точка фигуры перемещается
- 58. Скачать презентацию
- 59. Похожие презентации
Этот урок - урок Добра, Мудрости, Радости Во всем мне хочется дойти до самой сути. В работе, в поисках пути, В сердечной смуте.













































Слайд 4
Обучающая:
Закрепить знания по
осевой и центральной симметрии. Установить что такое параллельный перенос.
Учиться выполнять параллельный перенос и применять его при решении задач.Цели урока:
Слайд 5
Развивающая:
Развивать логическое мышление, умение
доказательно развивать свою мысль и умение делать выводы.
Цели урока:
Слайд 6
Воспитывающая:
Формирование умения работать в
коллективе. Воспитание умения делать собственный выбор. Воспитание любви к
природе и гордости за Родину.Цели урока:
Слайд 7
Валеологическая:
Создание оптимальных условий учебного процесса. Рациональное
чередование разных видов деятельности.
Цели урока:
Слайд 8
План урока
1. Организационный момент.
2. Задание на дом.
3. Проверка
домашнего задания
(опрос теории и математический диктант).
4. Актуализация
опорных знаний.5. Изучение новой темы.
6. Закрепление темы.
7. Разноуровневая практическая работа.
8. Итог урока.
Слайд 9
Задание на дом
п.116,
вопросы 14, 15
(стр. 281)
№1163(а), №1165
Принести циркуль и транспортир.
По желанию
сделать модель для параллельного переноса.
Слайд 11
Отображение плоскости на себя.
Выполняются следующие условия:
Каждой точке
плоскости ставится в соответствие какая-то одна точка этой же
плоскости.Каждая точка плоскости оказывается поставленной в соответствие какой-то точке этой же плоскости.
Слайд 12
Движение – отображение плоскости на себя, сохраняющее расстояние.
Осевая
и центральная симметрия – движения.
При движении:
отрезок отображается на равный
ему отрезоктреугольник отображается на равный ему треугольник
угол отображается на равный ему угол
луч отображается на луч
прямая отображается на прямую
любая фигура отображается на равную ей фигуру
Слайд 13
А1
А
l
Преобразование, при котором каждая точка А фигуры преобразуется
в симметричную ей относительно некоторой оси l точку А1,
при этом отрезок АА1 ┴ l и АК=КА1, называетсяосевой симметрией или
симметрией относительно прямой
К
А → А1 А1 = Sl(А)
Sl
Слайд 14
l
А≡А1
В
В1
К
Докажем, что осевая симметрия – движение.
Доказательство.
В ΔВАВ1 отрезок
АК – медиана и высота, значит ΔВАВ1 – равнобедренный
→ АВ = А1В1, ч.т.д.Слайд 15 В частности, если при осевой симметрии относительно прямой
l фигура Р переходит сама в себя, то она
называется симметричной относительно оси l, а ось l называется ее осью симметрии.Р
l
Слайд 16 Преобразование, переводящее каждую точку А фигуры в точку
А1, симметричную ей относительно центра О, называется центральной симметрией
или симметрией относительно точкиТочка О называется центром симметрии и является неподвижной. Других неподвижных точек это преобразование не имеет.
М
М1
О
М → М1 М1 = SО(М)
SO
Слайд 17
А1
В1
О
А
В
Докажем, что центральная симметрия – движение.
Доказательство.
В ΔАОВ и
ΔА1ОВ1:
АО=ОА1, ВО=ОВ1 (по построению)
(СУС) → АВ = А1В1, ч.т.д.
Слайд 18 Если при центральной симметрии относительно центра О фигура
Р преобразуется в себя, то она называется симметричной относительно
центра О.При этом центр О называется центром симметрии фигуры Р.
Р
O
Слайд 20 После падения Византии племянница ее последнего императора Софья
Палеолог бежала в Рим, а оттуда была выдана замуж
за великого князя московского Ивана III. Самым ценным приданым своей невесты жених считал ее родство с византийским императором, что давало ему повод объявить себя государем (царем) всея Руси. Двуглавый орел хорошо послужил государству Российскому как символ объединения русских земель вокруг богатого города и умного, волевого лидера.
Слайд 22
Симметрия вокруг нас
Симметричны снежинки, кристаллы, листья, цветы.
Симметричны животные, рыбы, птицы, насекомые.
Симметрично человеческое тело.
Слайд 31
Математический диктант.
1.
Отметьте точки К и М. Постройте точку К1, симметричную
точке К относительно точки М.
Слайд 32
2. Начертите прямую а и точку В вне
ее. Постройте точку В1, симметричную точке В относительно прямой
а.Слайд 33 3. Закончите предложение: «Преобразование фигуры F в фигуру
F1 называется движением, если оно ...».
Слайд 34 4. Треугольники АВС и МКР симметричны относительно
некоторой точки. Стороны ΔАВС равны 6 см, 4 см
и 7 см. Найти периметр Δ МКР.Слайд 35 5. Два ромба симметричны друг другу относительно некоторой
прямой. У первого ромба имеется прямой угол.
Будет ли второй ромб квадратом?Слайд 37 1. Отметьте точки М и К. Постройте точку
К1, симметричную точке К относительно точки М.
К
К1
М
Проверка диктанта
Слайд 38 2. Начертите прямую а и точку В вне
ее. Постройте точку В1, симметричную точке В относительно прямой
а.В1
В
а
Слайд 39 3. Закончите предложение: «Преобразование фигуры F в фигуру
F1 называется движением, если оно ...».
сохраняет расстояниеСлайд 40 4. Треугольники АВС и МКР симметричны относительно точки.
Стороны ΔАВС равны 6 см, 4 см и 7
см. Найти периметр Δ МКР.17 см
Слайд 41 5. Два ромба симметричны друг другу относительно прямой.
У первого ромба имеется прямой угол. Будет ли второй
ромб квадратом?Да
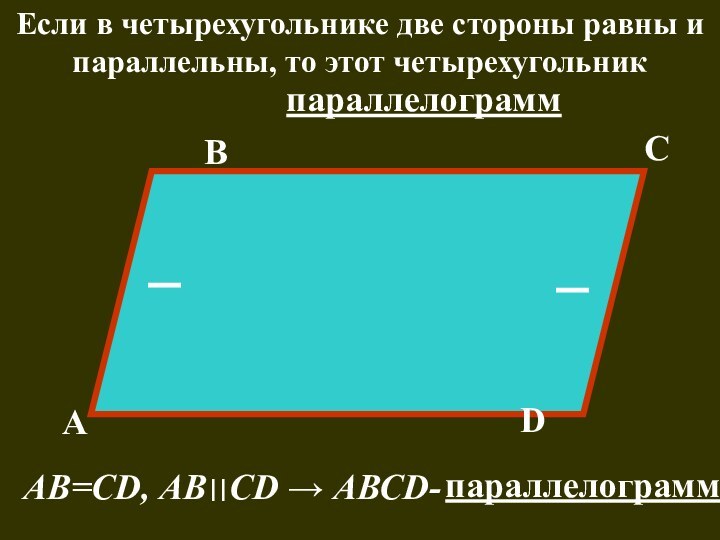
Слайд 44 Если в четырехугольнике две стороны равны и параллельны,
то этот четырехугольник
В
А
D
С
АВ=СD, АВ׀׀СD → АВСD-
параллелограмм
параллелограмм
Слайд 47 Преобразование, при котором каждая точка фигуры перемещается в
одном и том же направлении и на одно и
то же расстояние называется параллельным переносом.Чтобы задать параллельный перенос, достаточно задать некоторый вектор.
а
Слайд 48
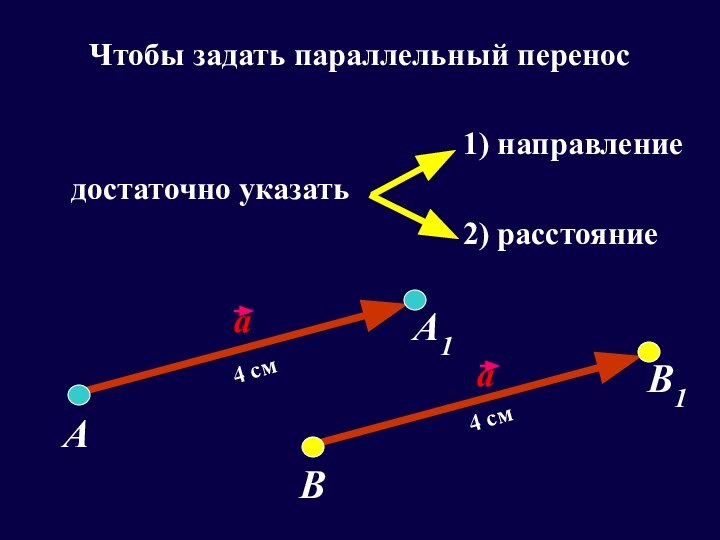
Чтобы задать параллельный перенос
1) направление
достаточно указать
2) расстояние
а
А
А1
4 см
а
В
В1
4 см
Слайд 53
Для параллельного переноса имеют место следующие свойства:
1) отрезок
переходит в
равный ему отрезок;2) угол переходит в
равный ему угол;
3) окружность переходит в
равную ей окружность;
4) любой многоугольник переходит в
равный ему многоугольник;
5) параллельные прямые переходят в
параллельные прямые;
6) перпендикулярные прямые переходят в
перпендикулярные прямые.
Слайд 55
Решим на закрепление:
Построить образы отрезка, треугольника и
четырехугольника при параллельном переносе.
Слайд 56
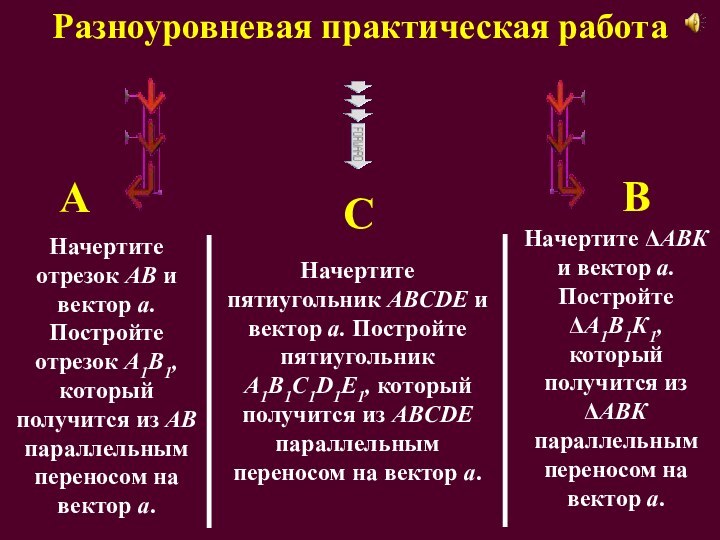
Разноуровневая практическая работа
А
С
В
Начертите отрезок АВ и вектор
a. Постройте отрезок А1В1, который получится из АВ параллельным
переносом на вектор a.Начертите ΔАВК и вектор a. Постройте ΔА1В1К1, который получится из ΔАВК параллельным переносом на вектор a.
Начертите пятиугольник AВCDE и вектор a. Постройте пятиугольник A1B1C1D1E1, который получится из AВCDE параллельным переносом на вектор a.
Слайд 57 Преобразование, при котором каждая точка фигуры перемещается в
одном и том же направлении и на одно и
то же расстояние называется параллельным переносом.Чтобы задать параллельный перенос, достаточно задать некоторый вектор.
а
а
M1 = Та (M)
М
М1





























