Презентация на тему Пересекающиеся плоскости

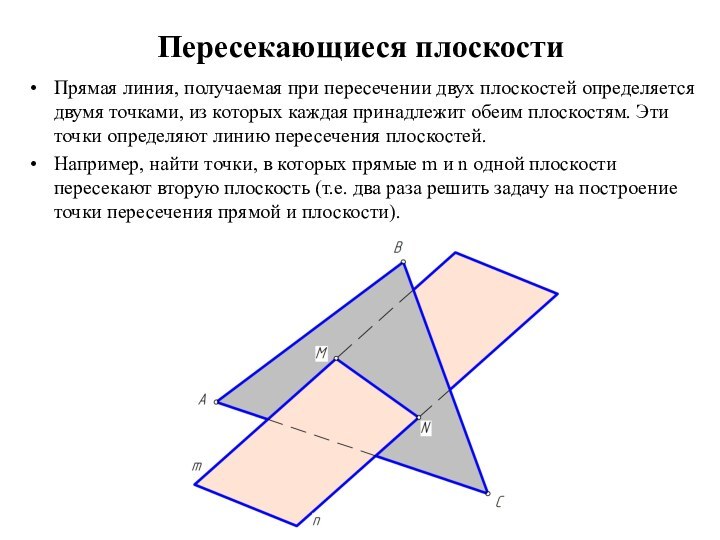
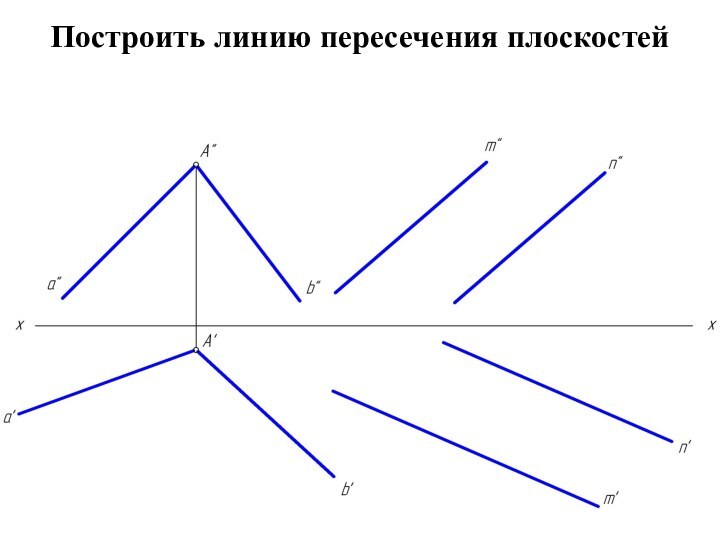
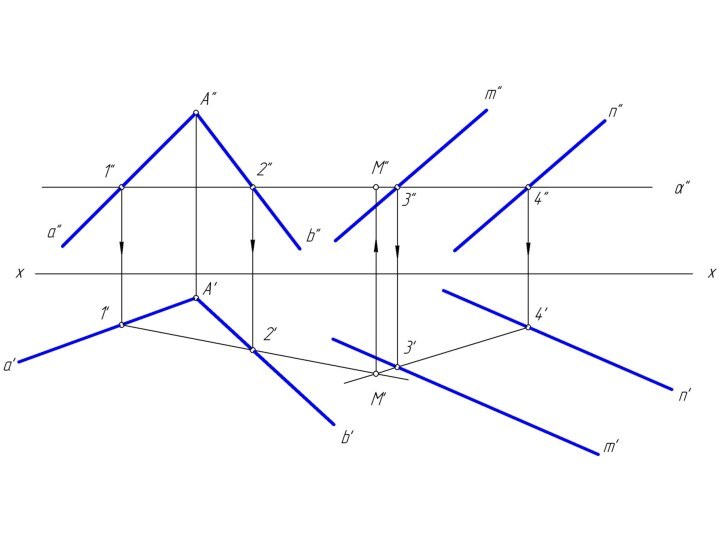
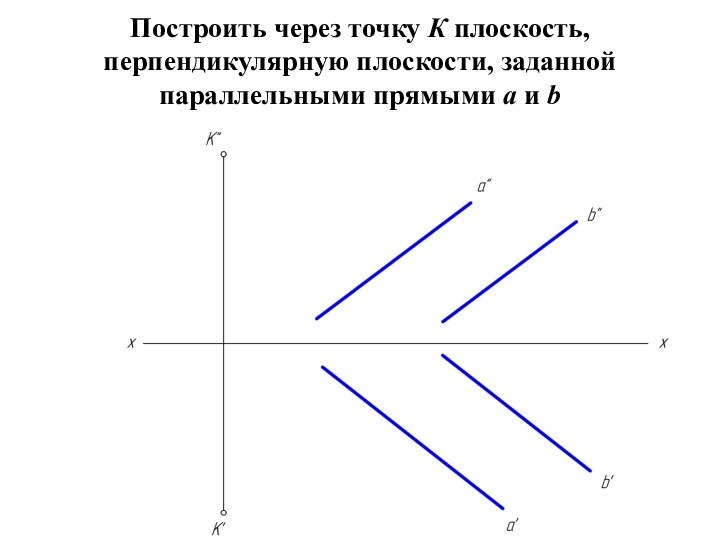
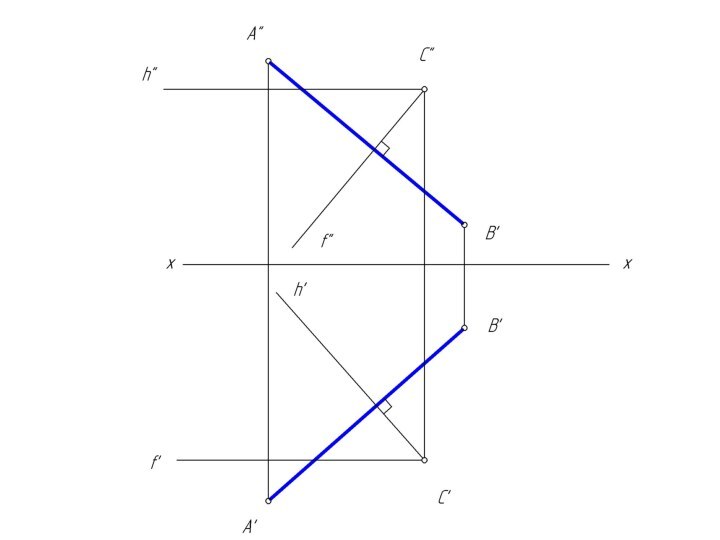
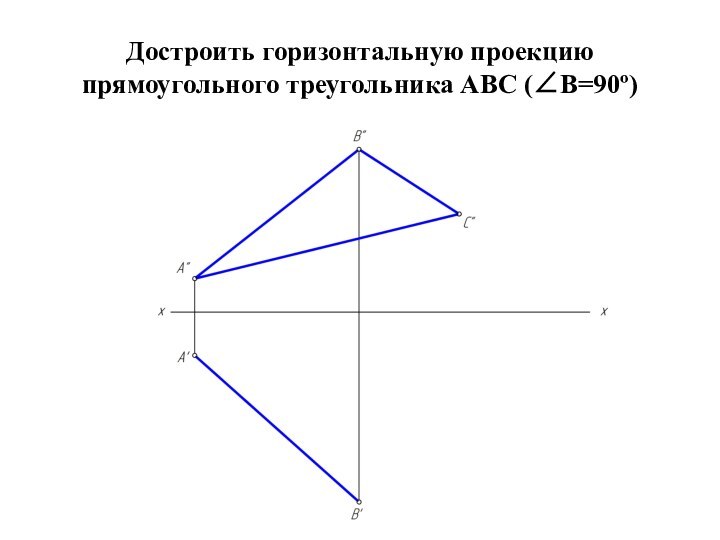
двумя пересекающимися прямыми a и b, назовем ее φ;
Вторая

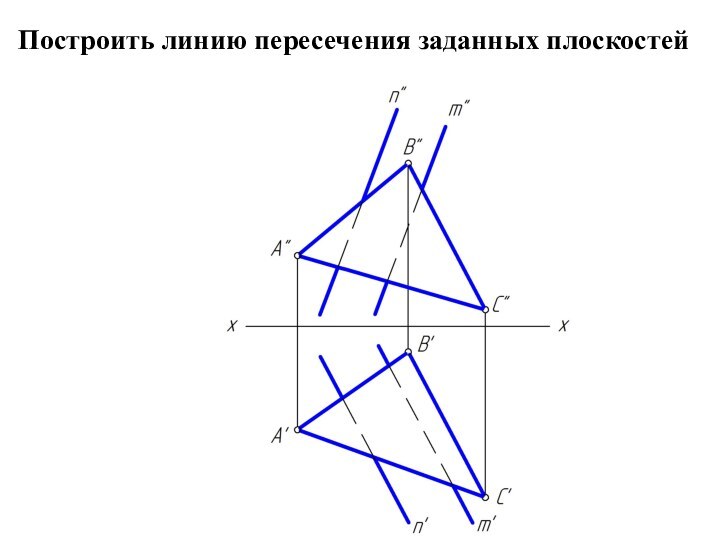
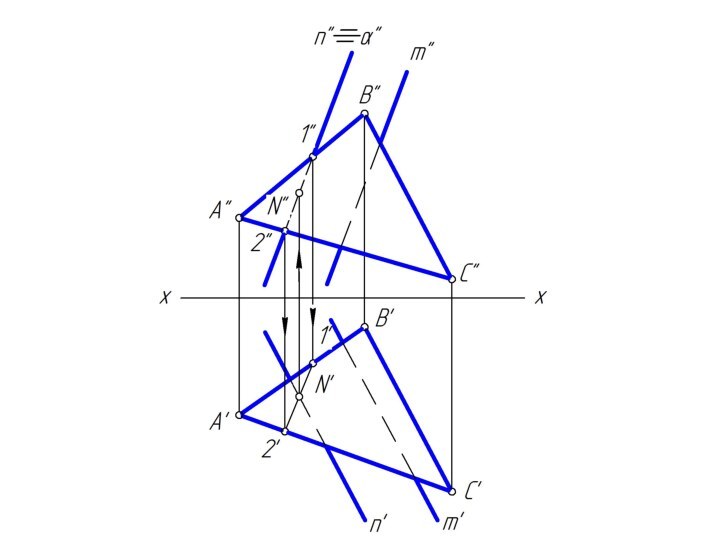
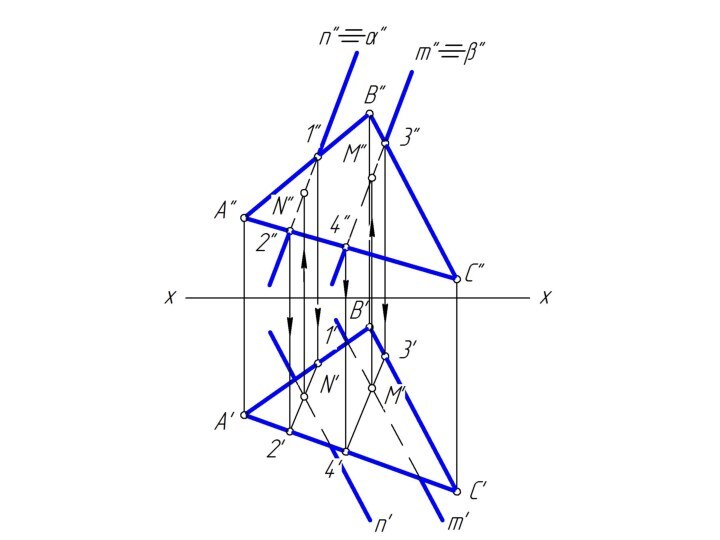
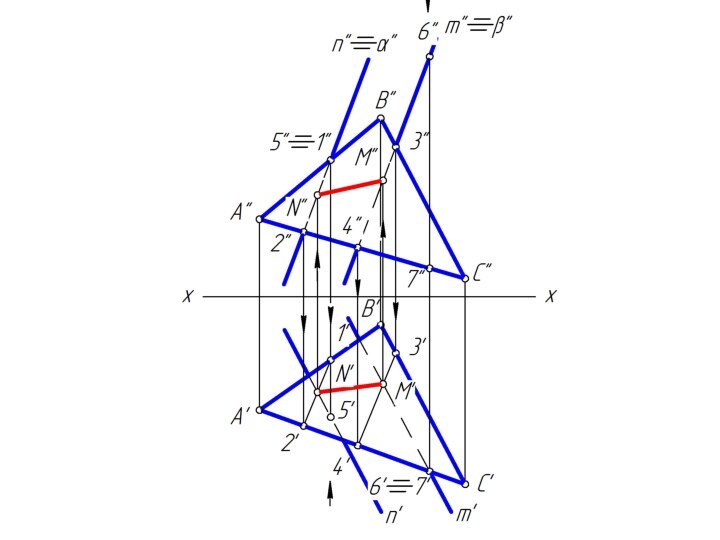
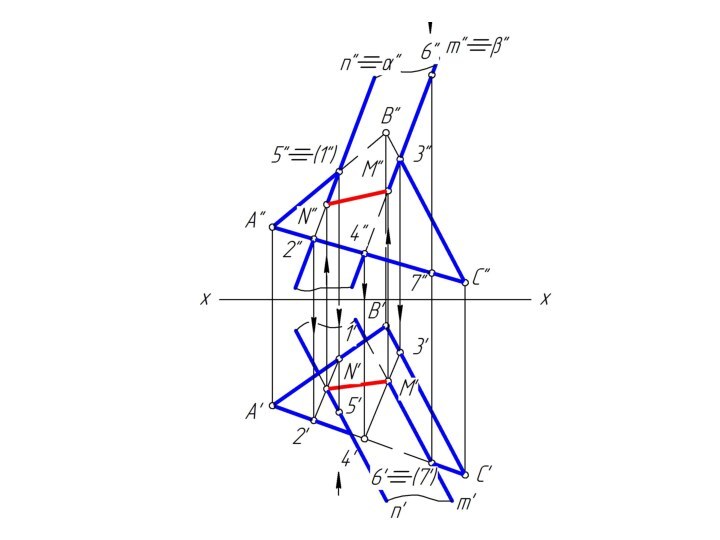
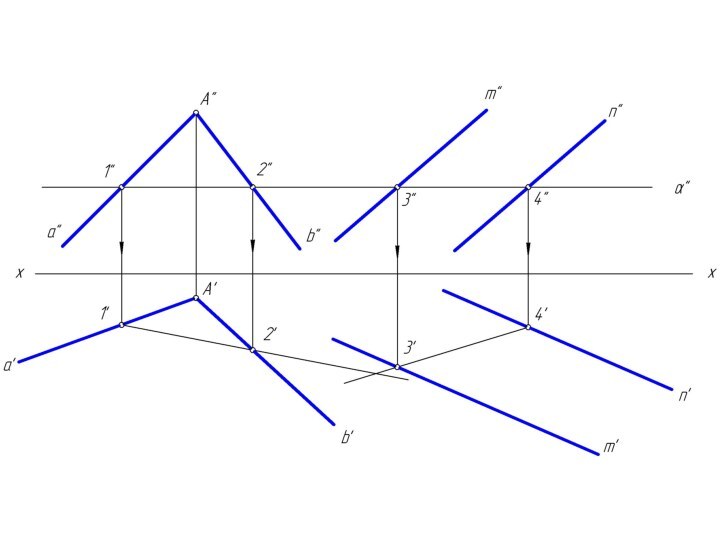
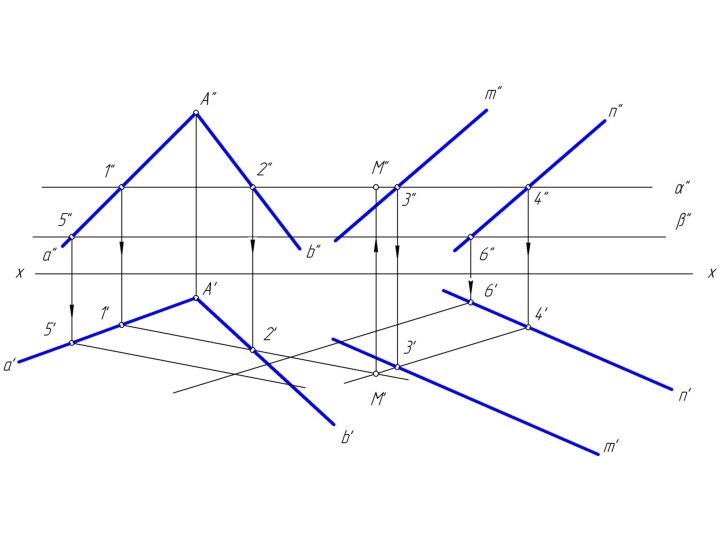
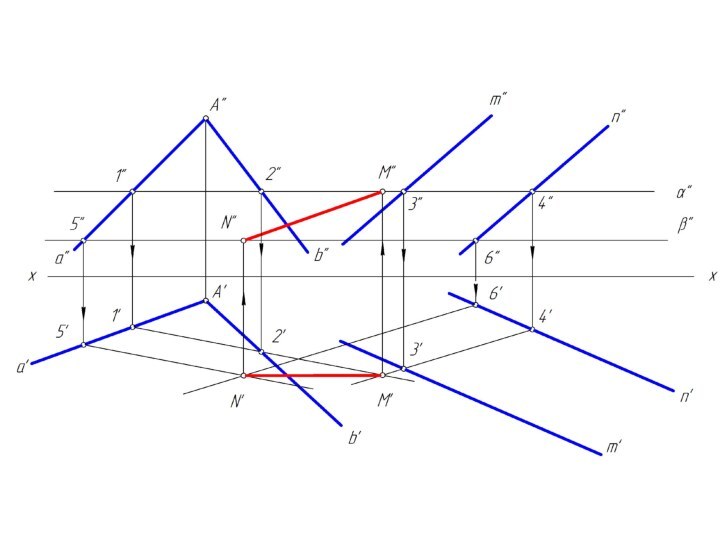
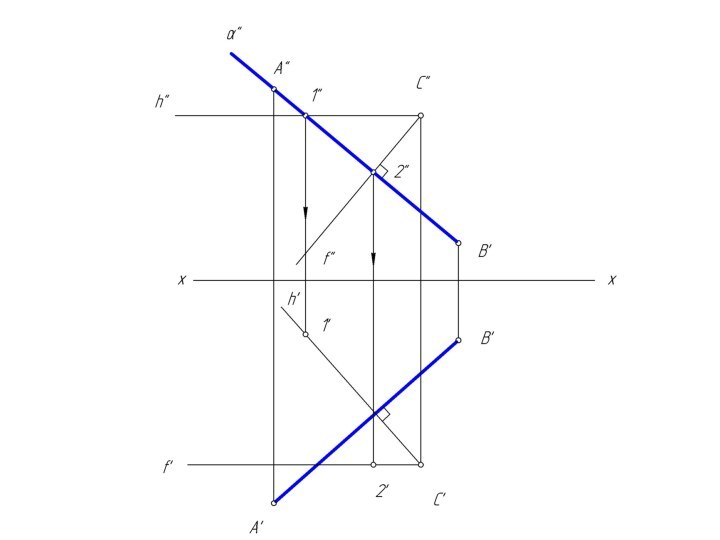
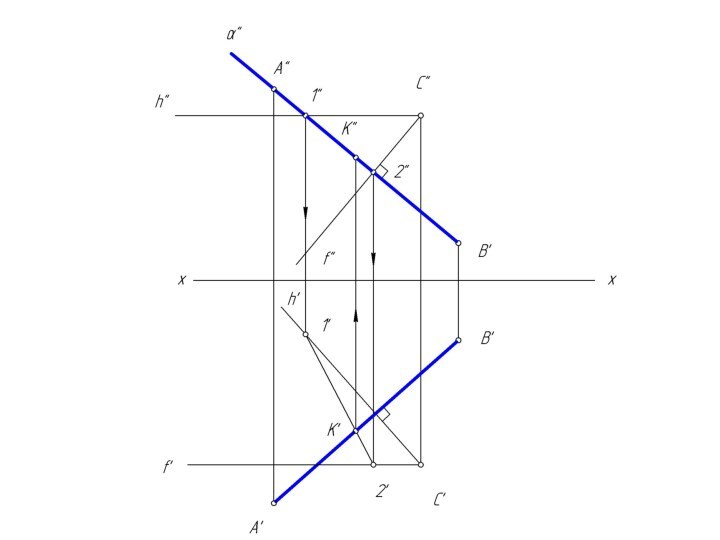
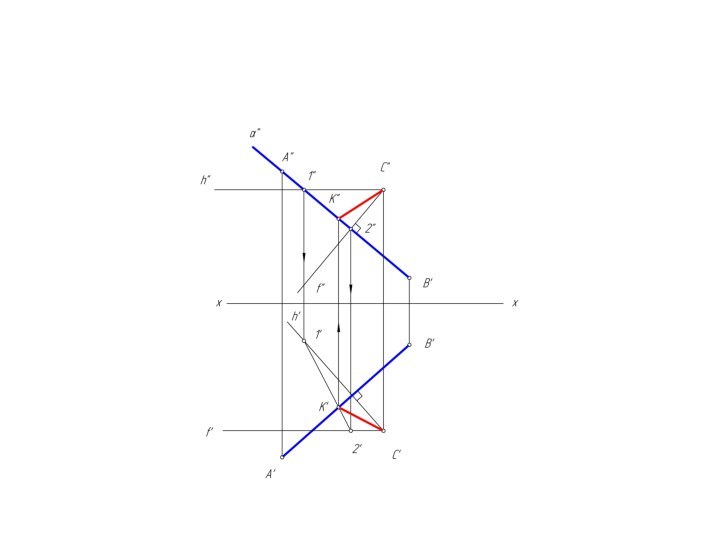
плоскость задана двумя параллельными прямыми m и n, назовем ее λ.
Чтобы найти две точки, принадлежащие одновременно двум заданным плоскостям φ и λ достаточно ввести две вспомогательные секущие плоскости α и β и выполнить последовательность операций:
(φ∩α) ∩ (λ∩α) = M; (φ∩β) ∩ (λ∩β) = N
Вспомогательным плоскостям α и β необходимо придать проецирующее положение, которое позволяет без дополнительных построений найти линию пересечения с заданными плоскостями φ и λ.

она перпендикулярна к двум пересекающимся прямым, принадлежащим этой плоскости.
Если

в плоскости взять не произвольные пересекающиеся прямые, а ее горизонталь и фронталь, то появляется возможность в этом случае воспользоваться теоремой о проецировании прямого угла.
Для того чтобы прямая (n) в пространстве была перпендикулярна плоскости, необходимо и достаточно, чтобы на эпюре горизонтальная проекция прямой (n') была перпендикулярна горизонтальной проекции горизонтали плоскости (h'), а фронтальная проекция прямой (n'') была перпендикулярна фронтальной проекции фронтали (f'') этой плоскости.
n'⊥h' и n''⊥f ''

из них содержит прямую, перпендикулярную к другой плоскости.
Поэтому построение

плоскости α, перпендикулярной плоскости β, можно осуществить двумя путями:
1. Проводим прямую m, перпендикулярную плоскости β, затем через прямую m проводим плоскость α;
2. Проводим прямую n, принадлежащую плоскости β, затем строим плоскость α, перпендикулярную прямой n.

плоскостей (первый путь решения), то задача имеет множество решений.
То

же самое происходит и при решении задачи по второму пути (в плоскости можно провести множество прямых n)
Чтобы конкретизировать задачу, необходимо указать дополнительные условия.

параллельными прямыми a и b

провести прямую, перпендикулярную отрезку АВ.
Перпендикуляр к плоскости перпендикулярен к

любой прямой, проведенной в этой плоскости. Исходя из этого можно наметить следующий алгоритм решения задачи:
1. через заданную точку С построить плоскость α, перпендикулярную отрезку АВ;
2. построить точку К пересечения отрезка АВ с плоскостью α;
3. отрезок СК перпендикулярен отрезку АВ.