Определение:
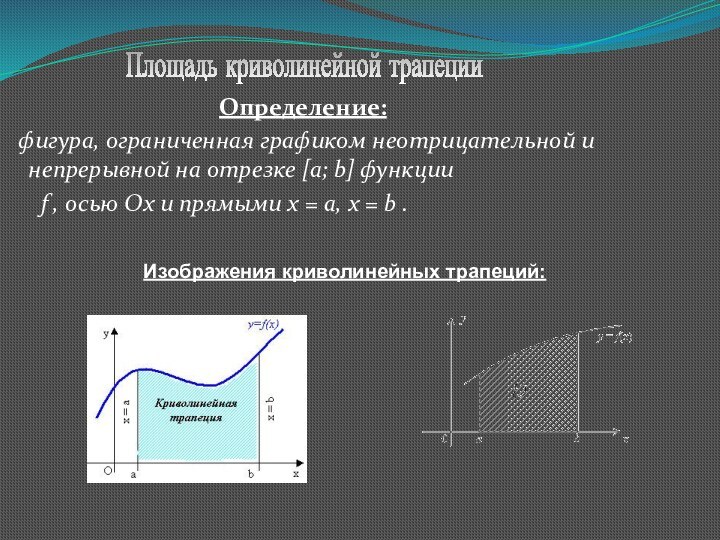
фигура, ограниченная графиком неотрицательной и непрерывной на отрезке [a; b] функции
f , осью Ох и прямыми х = а, х = b .
Площадь криволинейной трапеции
Изображения криволинейных трапеций:
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть

![Площадь криволинейной трапеции Если f – непрерывная и неотрицательная на отрезке [a; b]функция , а](/img/tmb/14/1308708/d89dd95689a2915d92137421a6ecfd7c-720x.jpg)
![Площадь криволинейной трапеции Доказательство Доказательство : Рассмотрим функцию S( x) , определенную наотрезке [a; b]](/img/tmb/14/1308708/45e1ba6e0391a4643ad4fba965bb7bea-720x.jpg)

![Площадь криволинейной трапеции Пусть на отрезке [а; b] оси Ох задана непрерывная функция f, не](/img/tmb/14/1308708/c2938125cb96a332cdfc88ef59dac662-720x.jpg)


![Площадь криволинейной трапеции ТЕОРЕМА. Пусть функция у=f(x) непрерывна на отрезке [a,b] и F(x)](/img/tmb/14/1308708/b4f146acc40234230e8e37b82d62c58e-720x.jpg)









Площадь криволинейной трапеции
Изображения криволинейных трапеций:
Теорема:
Теорема о вычислении площади криволинейной трапеции
Доказательство
Для вычисления площадей криволинейных трапеций применяется следующая теорема:
Теорема. Если f — непрерывная и неотрицательная на отрезке [а; b] функция, a F — ее первообразная на этом отрезке, то площадь S соответствующей криволинейной трапеции (рис. 2) равна приращению первообразной на отрезке [а; b] т. е.
S=F(b)-F(a). (1)
Доказательство. Рассмотрим функцию S (х), определенную на отрезке [а; b]. Если а
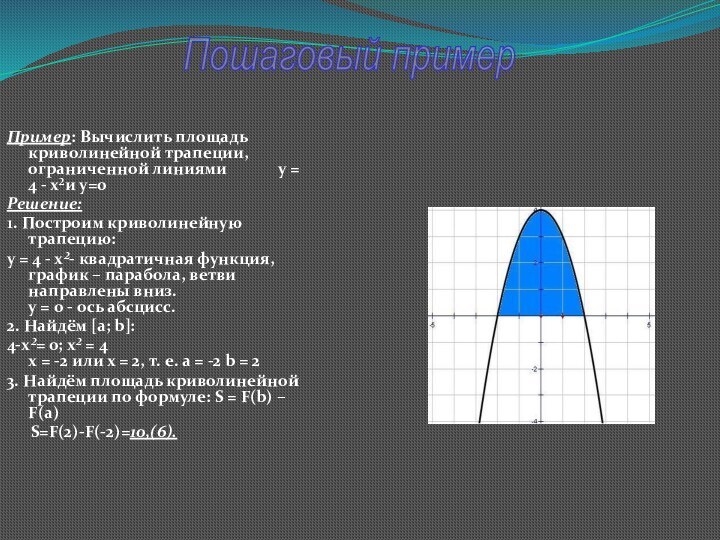
Пошаговый пример