Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Однопараметрические семейства линий

Содержание

2. Найти все точки плоскости ХоY,через которые: (а)
3. ax+by=p Например, уравнение
4. y-b=p(x-a) Например, уравнение
5. (x-a)²+(y-b)²=p Например, уравнение x²+2x+y²-6y+p=0(x+1)²+(y-3)²=10-p задает (при p
6. x²+y²=px Семейство окружностей радиуса 1/2׀p׀ c центром
7. x²+y²=py Семейство окружностей радиуса1/2׀p׀ c центром на
8. (x-a)(y-b)=p При p=0 уравнение задает пару пересекающихся
9. y=f(x-p) y-p=f(x) Например, (x-p)²+(y-1)²=4 задает семейство окружностей
10. y=f(x/p) y/p=f(x) На рисунке представлено семейство парабол
11. Определить вид семейства линий, заданных
12. y= -x²+4px+2-3p-4p²Ясно, что это параболы с ветвями,
13. Скачать презентацию
14. Похожие презентации

Найти все точки плоскости ХоY,через которые: (а) проходит только одна парабола; (б) не проходит ни одна парабола; (в) проходит более одной параболы семейства y=x²+(4p+2)x+2p²

Главная
Математика
Однопараметрические семейства линий

Научно-исследовательская работа по математике ОДНОПАРАМЕТРИЧЕСКИЕ СЕМЕЙСТВА ЛИНИЙ Автор: Гуркин Александр Александрович,

Найти все точки плоскости ХоY,через которые: (а) проходит только одна парабола; (б)

ax+by=p Например, уравнение x-2y=p задает семейство

y-b=p(x-a) Например, уравнение y+2=p(x-3) задает семейство

(x-a)²+(y-b)²=p Например, уравнение x²+2x+y²-6y+p=0(x+1)²+(y-3)²=10-p задает (при p

x²+y²=px Семейство окружностей радиуса 1/2׀p׀ c центром на оси oX в точке

x²+y²=py Семейство окружностей радиуса1/2׀p׀ c центром на оси oУ в точке (0;

(x-a)(y-b)=p При p=0 уравнение задает пару пересекающихся прямых: x=b и y=p. При

y=f(x-p) y-p=f(x) Например, (x-p)²+(y-1)²=4 задает семейство окружностей радиуса R=2 с центром в

y=f(x/p) y/p=f(x) На рисунке представлено семейство парабол y=p(x²-2x) для значений р=1,p=3,p=1/2,

Определить вид семейства линий, заданных данными уравнениями, и нарисовать несколько

y= -x²+4px+2-3p-4p²Ясно, что это параболы с ветвями, направленными вниз:y=-(x-2p)²+2-3p вершина которых V

y=x²+(4p+2)x+2p² p=1,p=0,p=-1,p=-2y=2x-x²(огибающая)(б) Д2х-х², тогда квадратное уравнение имеет два решения Р1,2= - х

Слайды презентации

Слайд 2 Найти все точки плоскости ХоY,через которые: (а) проходит только

Найти все точки плоскости ХоY,через которые: (а) проходит только одна парабола;

одна парабола; (б) не проходит ни одна парабола; (в) проходит более

одной параболы семейства

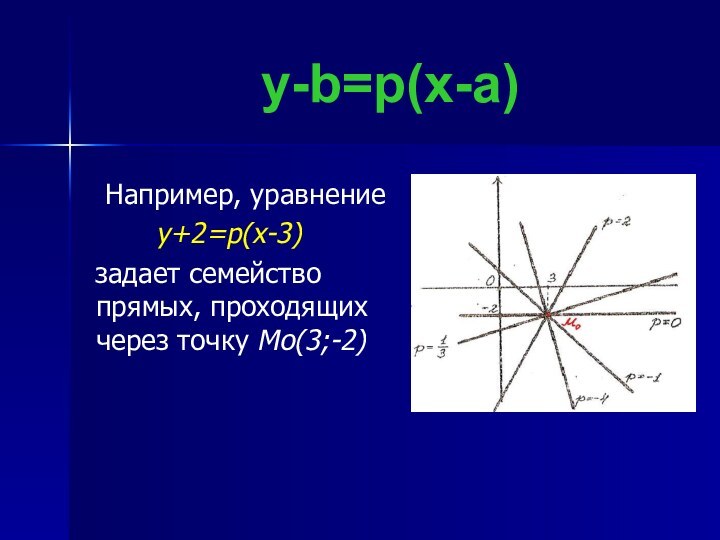
y=x²+(4p+2)x+2p²

Слайд 3 ax+by=p
Например, уравнение

ax+by=p Например, уравнение x-2y=p задает семейство прямых с

x-2y=p
задает семейство прямых с угловым коэффициентом

k=1/2 и пересекающих ось oX в точке (0; - p /2)

Слайд 4 y-b=p(x-a)
Например, уравнение
y+2=p(x-3)

задает семейство прямых, проходящих через точку

Mo(3;-2)

Слайд 5 (x-a)²+(y-b)²=p
Например, уравнение
x²+2x+y²-6y+p=0(x+1)²+(y-3)²=10-p задает (при

p

З)

Слайд 6 x²+y²=px
Семейство окружностей радиуса 1/2׀p׀ c центром на

x²+y²=px Семейство окружностей радиуса 1/2׀p׀ c центром на оси oX в

оси oX в точке (p /2;0). Все они проходят

через начало координат.
Действительно, x²+y²=px<=>(x-p/2)²+y²=p²/2

Слайд 7 x²+y²=py
Семейство окружностей радиуса1/2׀p׀ c центром на оси

x²+y²=py Семейство окружностей радиуса1/2׀p׀ c центром на оси oУ в точке

oУ в точке (0; p /2); все они также

проходят через начало координат.

Слайд 8 (x-a)(y-b)=p
При p=0 уравнение задает пару пересекающихся прямых:

(x-a)(y-b)=p При p=0 уравнение задает пару пересекающихся прямых: x=b и y=p.

x=b и y=p. При p≠0 это две ветви гиперболы-y=b(

p/x-a)
Ее асимптотами являются вышеуказанные прямые x=a и y=b точка пересечения которых является их центром симметрии. При р>0 гипербола занимает первую и третью четверти (относительно асимптот),

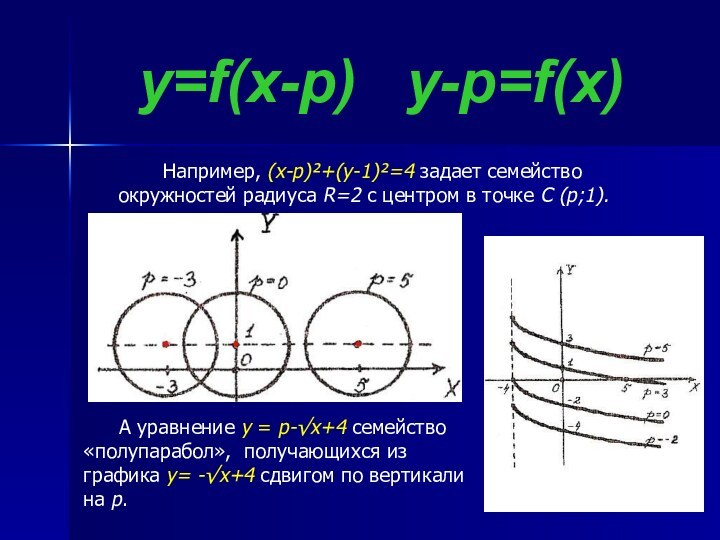
семейства (x+3)(y+2)=p для значений p=0, p= -4, p=6, p=15.

а при p <0 - вторую и четвертую на рисунке представлены линии

Слайд 9 y=f(x-p) y-p=f(x)
Например, (x-p)²+(y-1)²=4 задает семейство окружностей радиуса

R=2 с центром в точке С (p;1).
А уравнение

у = p-√x+4 семейство «полупарабол», получающихся из графика y= -√x+4 сдвигом по вертикали на p.

Слайд 10 y=f(x/p) y/p=f(x)
На рисунке представлено семейство парабол y=p(x²-2x)

y=f(x/p) y/p=f(x) На рисунке представлено семейство парабол y=p(x²-2x) для значений р=1,p=3,p=1/2, p=-1,p=

для значений р=1,p=3,p=1/2, p=-1,p= -2 и p=0 (это

прямая у=0).
Все параболы этого семейства пересекают ось оХ при х=0 и x = 2.

Слайд 11 Определить вид семейства линий, заданных данными уравнениями,

и нарисовать несколько типичных линий
(x+p-2)²+(y-p²/4+1)²=9
семейства, отвечающих конкретным значениям р
Данное

уравнение представляет собой окружность радиуса R=3 с центром в точке С с координатами x= -p+2 y=p²/4-1. Исключив из этой системы параметр p , получим уравнение y=1/4(x-2)²-1. Значит, все центры этих окружностей лежат на параболе y=(1/4)x²-x

р=0 (с центром С(2; -1) ), р=2 (с центром С(0;0) ), р=4(с центром С(6;3) ), р=5 (с центром С(-3;5 ¼)).

Слайд 12 y= -x²+4px+2-3p-4p²
Ясно, что это параболы с ветвями, направленными

y= -x²+4px+2-3p-4p²Ясно, что это параболы с ветвями, направленными вниз:y=-(x-2p)²+2-3p вершина которых

вниз:y=-(x-2p)²+2-3p вершина которых V имеет координаты x=2p y=2-3p

исключив параметр р из предыдущей системы, получим y=2-3|2x

Т. е. все вершины парабол лежат на Прямой y=2-3|2 x.Поскольку
коэффициент при х² постоянен (равен -1), то все параболы имеют одинаковую форму, т.е. получаются друг из ,друга параллельным переносом.

Здесь представлены параболы семейства при
р=0, р=4 и р= -2.