Слайд 2
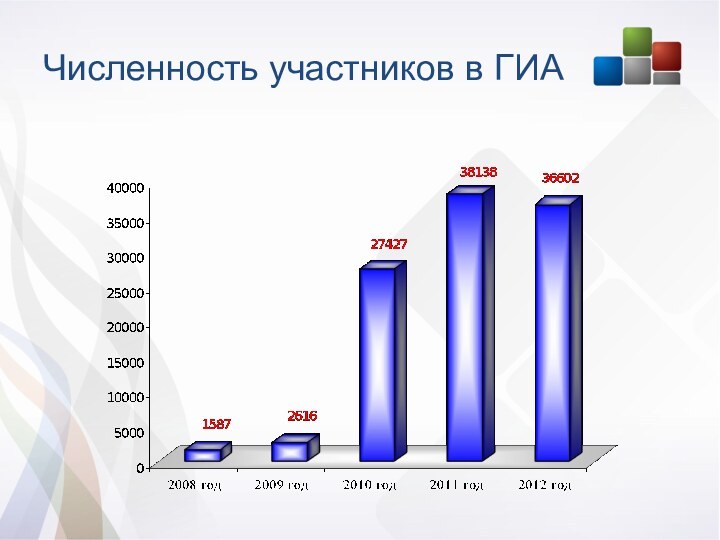
Численность участников в ГИА
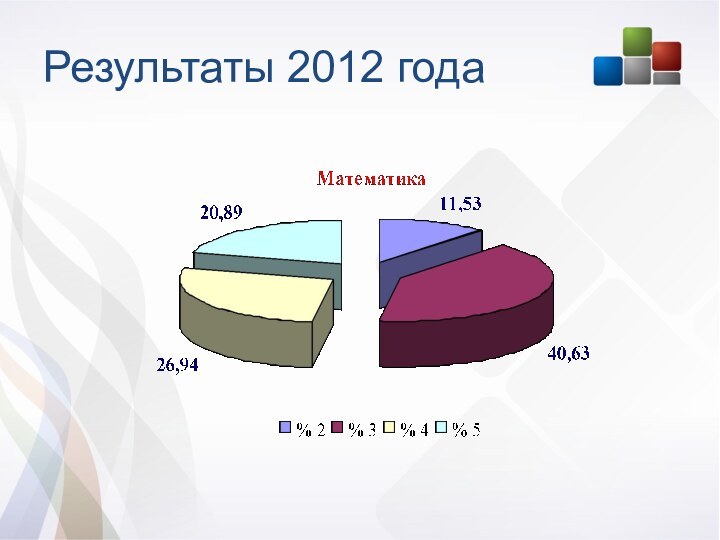
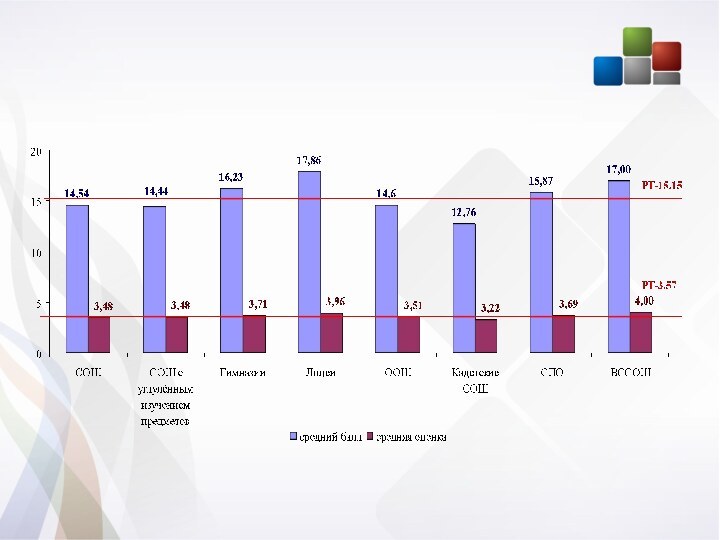
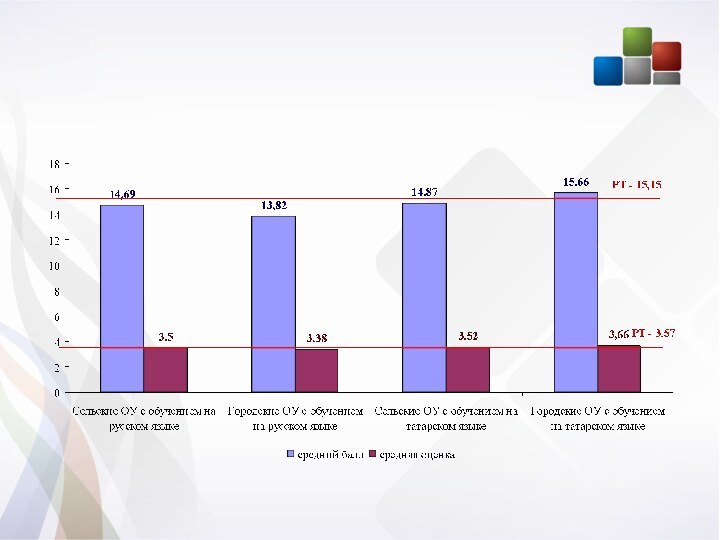
Слайд 4
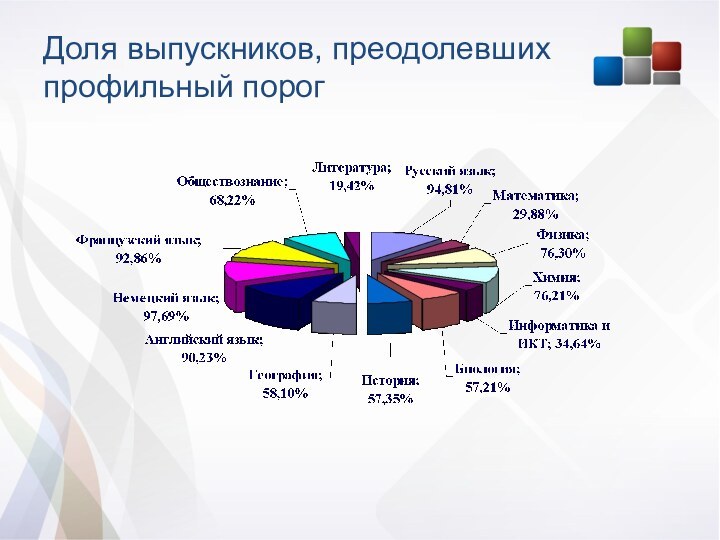
Доля выпускников, преодолевших профильный порог
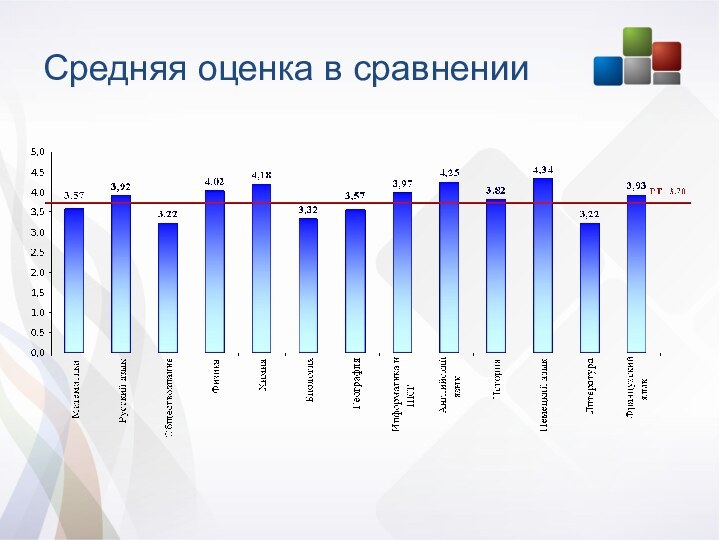
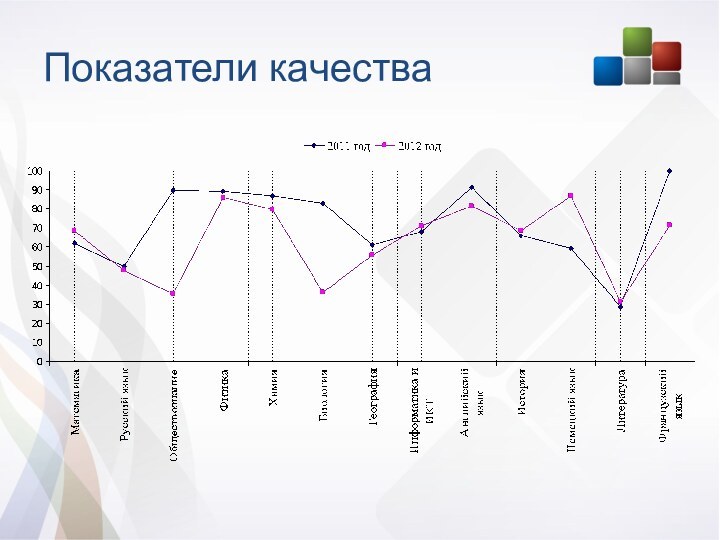
Слайд 9
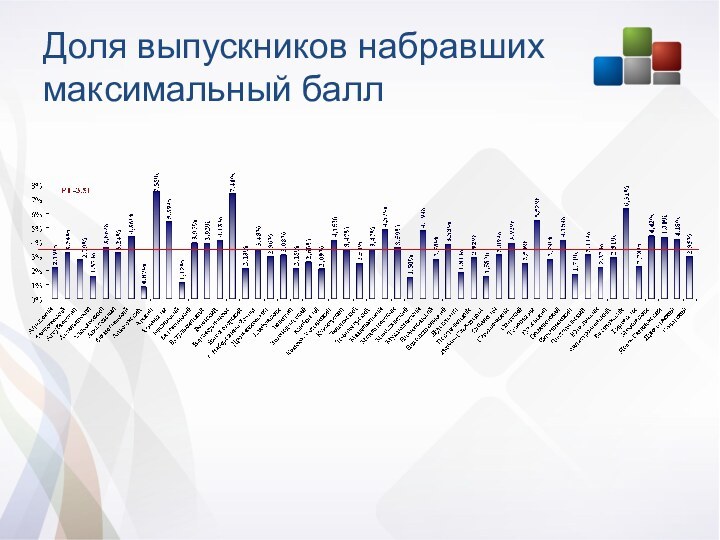
Доля выпускников набравших максимальный балл
Слайд 10
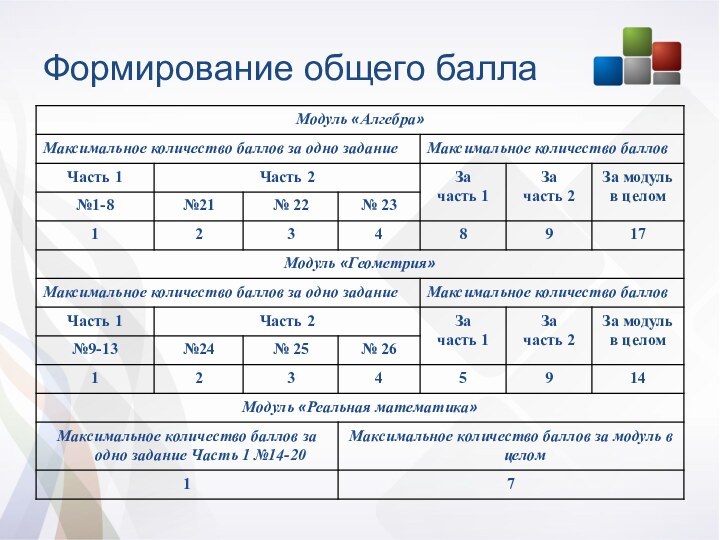
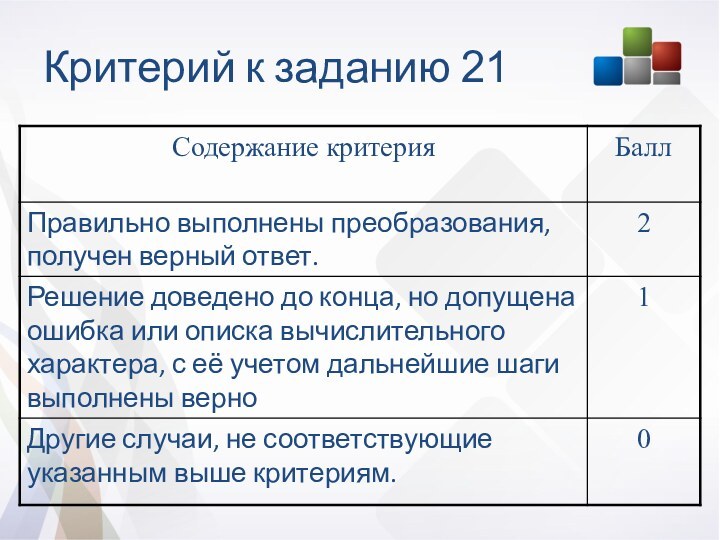
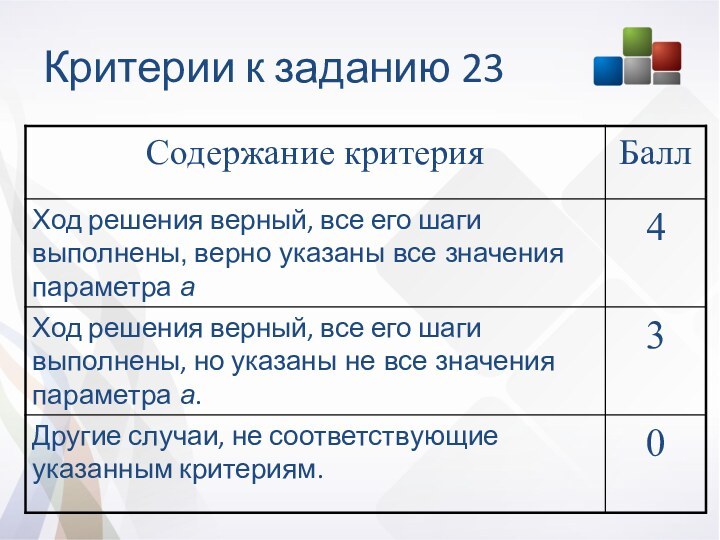
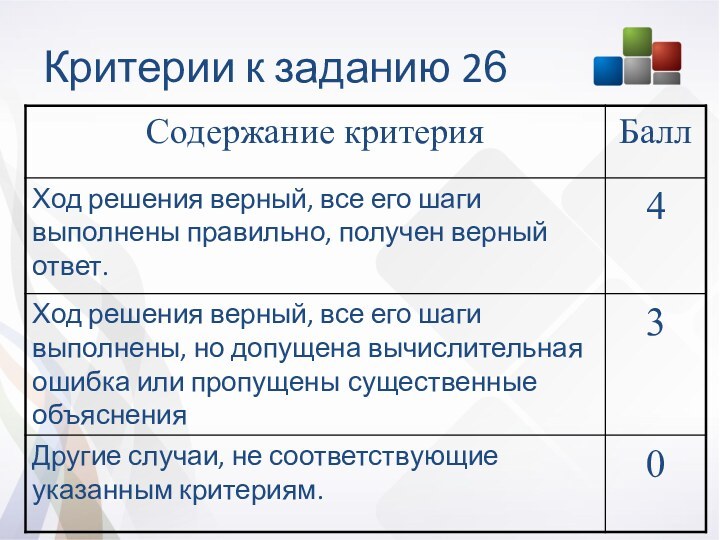
Структура и характеристика
Работа состоит из трёх модулей: «Алгебра»,
«Геометрия», «Реальная математика». Модули выполняются последовательно.
Общее время экзамена 235
минут
Всего в работе 26 заданий:
- 20 заданий базового уровня
6 заданий повышенного уровня
Максимальный балл за работу 38
Слайд 12
Минимальный критерий
8 баллов:
- не менее 3 баллов
по модулю «Алгебра»
- не менее 2 баллов по
модулю «Геометрия»
- не менее 2 баллов по модулю «Реальная математика»
Слайд 13
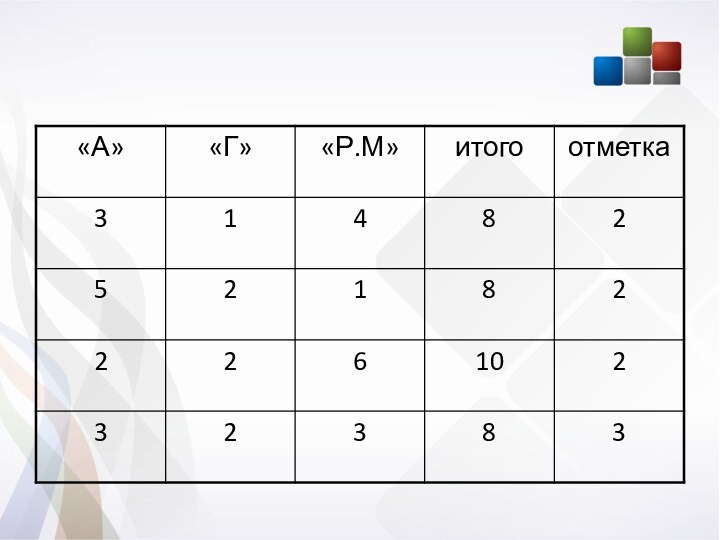
Схема перевода в 5-балльную шкалу отметок
Слайд 15
Дополнительные материалы
Справочные материалы, содержащие основные формулы курса математики,
и выдаваемые вместе с работой.
Линейка
Калькулятором пользоваться нельзя!!!
Слайд 17
1. Общие положения
1.1 Бланк заполняется чёрной гелевой ручкой
1.2
Бланки ответов (№1 и №2) индивидуальные. Обмен бланками не
допускается.
При получении бланка заполните следующие поля:
Фамилия, имя и отчество
Подпись
Номер варианта
Ответы на задания (Бланк №1)
Замена ошибочных ответов (Бланк №1)
Поле для записи развернутых ответов (Бланк №2)
Подпись должна помещаться в отведенном для нее поле.
Не разрешается делать любые пометки, исправления и записи вне указанных полей.
Слайд 18
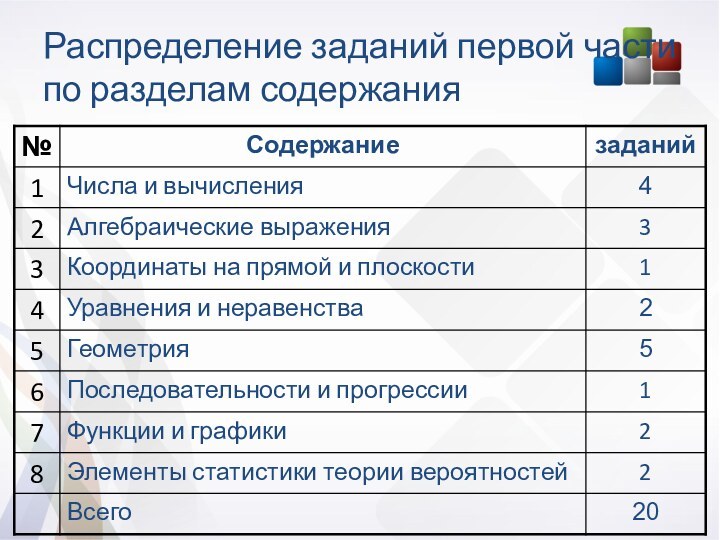
Распределение заданий первой части по разделам содержания
Слайд 19
Уровни сложности
Планируемые показатели трудности заданий первой части работы
находятся в диапазоне от 60% до 95%: 8 заданий
уровня 80-90%, 8 задания уровня 70-80% и 4 задания уровня 60-70%.
Планируемый уровень трудности заданий второй части: 21(40-50%), 22(20-40%),
23(10-20%), 24(40-50%), 25(20-40%),
26(10-20%)
Слайд 20
Сопоставьте числовые выражения и принимаемые ими значения:
1) 0,002
2) 0,2
3) -0,2
4) -0,002
Слайд 21
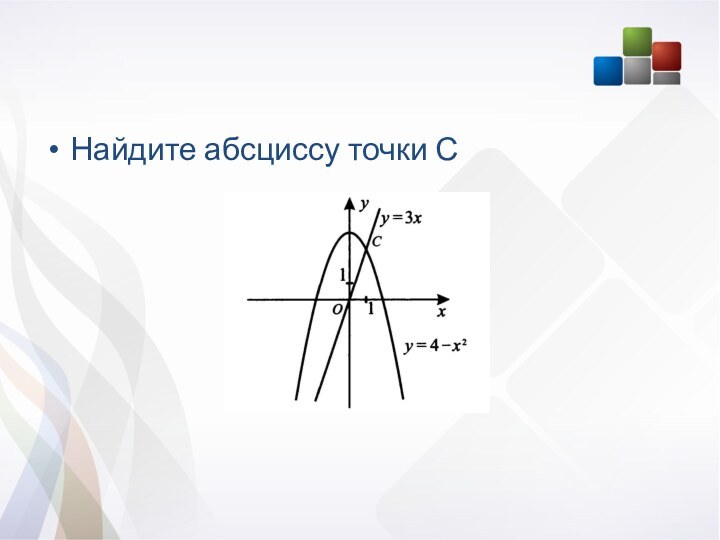
На координатной прямой отмечены числа а и b
. Какое из приведенных утверждений неверно?
Слайд 22
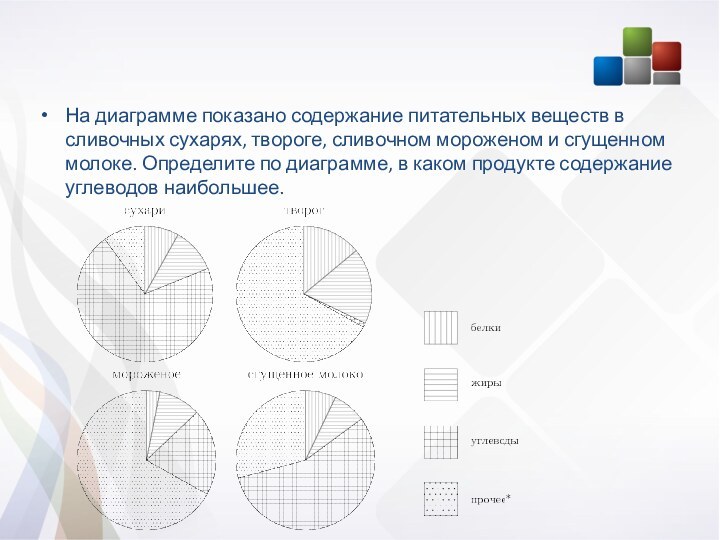
На диаграмме показано содержание питательных веществ в сливочных
сухарях, твороге, сливочном мороженом и сгущенном молоке. Определите по
диаграмме, в каком продукте содержание углеводов наибольшее.
Слайд 23
Средний балл тестирования
учащихся 9 классов по математике
Укажите
номера верных утверждений
Худшие результаты у учащихся Туниса
Только у 2
государств средний балл выше 500
Учащиеся 2 государств имеют одинаковый средний балл
У учащихся 3 государств средний балл не менее 460
Слайд 24
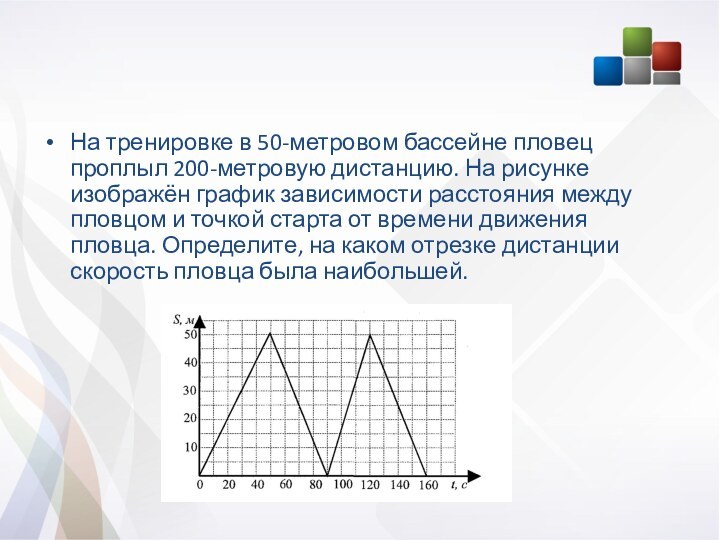
На тренировке в 50-метровом бассейне пловец проплыл 200-метровую
дистанцию. На рисунке изображён график зависимости расстояния между пловцом
и точкой старта от времени движения пловца. Определите, на каком отрезке дистанции скорость пловца была наибольшей.
Слайд 25
На одном из рисунков изображена гипербола. Укажите номер
этого рисунка
1) 2) 3) 4)
Слайд 27
Задачи на вероятность
Телевизор у Саши сломался и показывает
только один случайный канал. Саша включает телевизор. В это
время по пятнадцати каналам из пятидесяти показывают кинокомедии. Найдите вероятность того, что Саша попадет на канал, где комедия не идет.
На тарелке 30 пирожков: 3 с мясом, 24 с капустой и 3 с вишней. Леша наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
В полуфинал соревнований вышли 12 спортсменов, выступающих за различные спортивные клубы: 6 за ЦСКА, 4 за Спартак, 2 за Динамо. Порядок выступления определяется жеребьёвкой. Какова вероятность того, что завершать выступления будут спортсмен из ЦСКА?
В новогоднем подарке 7 шоколадных конфет, 9 ирисок, 15 карамелек и 4 леденца. Какова вероятность первой достать шоколадную конфету?
Слайд 28
Геометрия
Какие из следующих утверждений верны?
1) Угол опирающийся на
диаметр окружности – прямой.
2) Диагонали параллелограмма равны.
3) Сумма
двух противоположных углов четырехугольника не превосходит 180 градусов.
4) Если в параллелограмме диагонали перпендикулярны, то это — ромб.
Слайд 29
Геометрия
Мальчик прошел от дома по направлению на запад
720 м. Затем повернул на юг и прошел 300
м. На каком расстоянии (в метрах) от дома оказался мальчик?
Какой угол (в градусах) образуют минутная и часовая стрелки часов в 5 ч?
Человек ростом 1,5 м стоит на расстоянии 6 м от столба, на котором висит фонарь на высоте 10,5 м. Найдите длину тени человека в метрах.
Сколько потребуется кафельных плиток квадратной формы со стороной 20 см, чтобы облицевать ими стену, имеющую форму прямоугольника со сторонами 2,6 м и 3,6 м?
Слайд 30
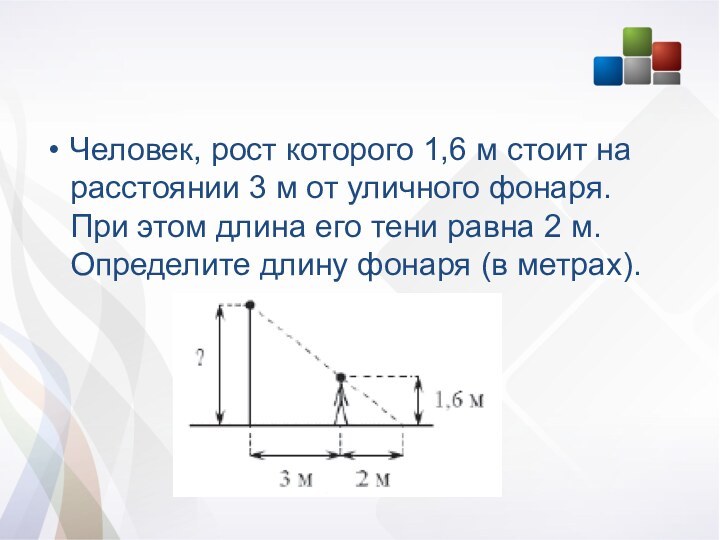
Человек, рост которого 1,6 м стоит на расстоянии
3 м от уличного фонаря. При этом длина его
тени равна 2 м. Определите длину фонаря (в метрах).
Слайд 31
Часть 2
Сократите дробь
Решите систему уравнений
Разложите на множители
Какое из
Слайд 32
При каких значениях р вершины парабол
и
расположены по разные стороны от оси ох?
Известно, что графики функций
и имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
Слайд 33
Найдите наибольшее значение выражения
При каких значениях х и
у оно достигается?
Найдите наименьшее значение выражения
При каких значениях х
и у оно достигается?
Слайд 34
Часть 2
Смешав 40-процентный и 90-процентный растворы кислоты и
добавив 10 кг чистой воды, получили 62-процентный раствор кислоты.
Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 72-процентный раствор кислоты. Сколько килограммов 40-процентного раствора использовали для получения смеси?
Теплоход идёт по течению реки в 5 раз медленнее, чем скутер против течения, а по течению скутер идёт в 9 раз быстрее, чем теплоход против течения. Во сколько раз собственная скорость скутера больше собственной скорости теплохода?
Слайд 35
Задания с графиками
Постройте график функции
И определите, при
каких значениях с прямая у=с имеет с графиком ровно
три общие точки.
Слайд 36
Геометрия
Основания трапеции равны 6 и 10, а боковые
стороны 2 и 4. Биссектрисы углов при одной стороне
пересекаются в точке А, а при другой – в точке В. Найдите АВ.
На окружности лежат четыре точки А, B, С, D в указанном порядке. Точки K, L, M, N – середины дуг АВ, ВС, СD, DА соответственно. Докажите, что КМ и LN перпендикулярны.
Слайд 37
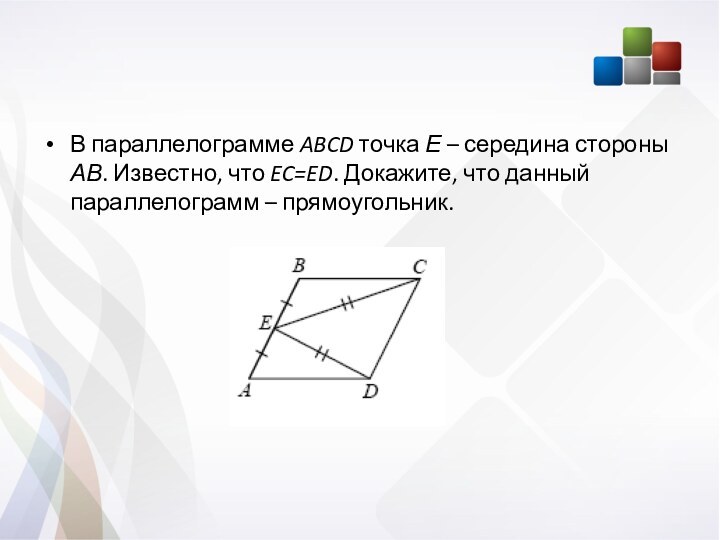
В параллелограмме ABCD точка Е – середина стороны
АВ. Известно, что EC=ED. Докажите, что данный параллелограмм –
прямоугольник.
Слайд 38
Одна из биссектрис треугольника делится точкой пересечения биссектрис
в отношении 3:2, считая от вершины. Найдите периметр треугольника,
если длина стороны треугольника, к которой эта биссектриса проведена, равна 12 см.