Слайд 2
Понятие рационального числа
Рациональные числа - это натуральные, отрицательные
и дробные (обыкновенные и конечные десятичные) числа.
От английского "ratio"
- отношение,соотношение.
Примеры рациональных чисел:
Слайд 3
Историческая справка
“ К созданию понятия отрицательного числа китайские

ученые подошли раньше математиков других народов, во II в.
до н. э. Положительные количества в китайской математике называли “чжен”, отрицательные – “фу”. Их изображали разными цветами: “ чжен” - красным, “ фу” - черным. Такой способ изображения использовался в Китае до середины ХII столетия, пока Ли Е не предложил более удобное обозначение отрицательных чисел - цифры, которые изображали отрицательные числа перечеркивали черточкой справа налево. Введение отрицательных чисел и правил их сложения и вычитания можно считать одним из самых крупных открытий китайских ученых”
“ В Европе с сознанием уверенности в справедливости своих вычислений начал оперировать с отрицательными числами французский математик Никола Шюке. В своих трудах в 1484 г. Он рассматривает задачи, приводящие к уравнениям с отрицательными корнями. Шюке заявляет, что “это вычисление, которое иные считают невозможным, правильно”.
Чех Ян Видман уже писал “+” и “ - ” для сложения и вычитания. А чуть позднее немецкий ученый Михель Штофель написал “Полную Арифметику”, которая была напечатана в 1544 году. В ней встречаются такие записи для чисел: 0 – 2; 0 + 2; 0 – 5; 0 + 7. Всеобщее признание отрицательные числа получили в первой половине XIX в., когда была развита строгая теория положительных и отрицательных чисел.
Слайд 4
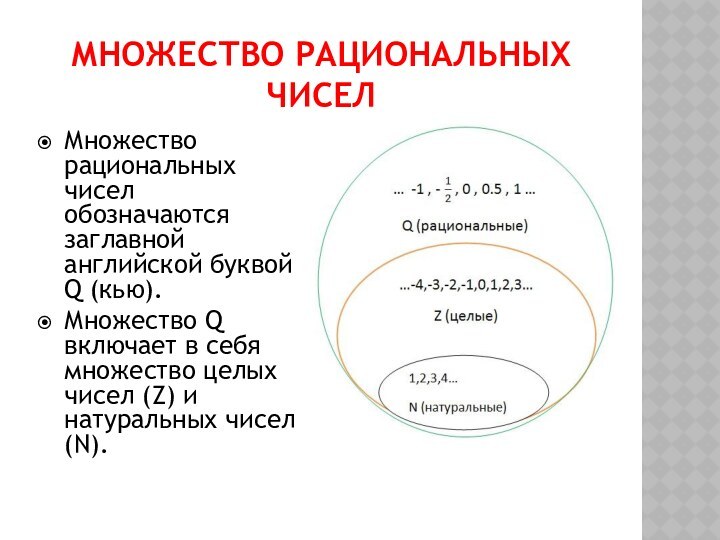
Множество рациональных чисел
Множество рациональных чисел обозначаются заглавной английской
буквой Q (кью).
Множество Q включает в себя множество целых
чисел (Z) и натуральных чисел (N).
Слайд 5
рациональное число
Любое рациональное число можно представить в виде
дроби, у которой числитель принадлежит целым числам, а знаменатель
- натуральным.
a/b, где a ∈ Z ( a принадлежит целым числам ), b∈N ( b принадлежит натуральным числам ).
Слайд 6
Сравнение рациональных чисел
Сравнение рациональных чисел — это сравнение
чисел положительных и отрицательных, целых и дробных (обыкновенные дроби
и десятичные дроби).
Из двух рациональных чисел больше то, которому на числовой оси соответствует точка, расположенная правее.
Всякое положительное число больше 0.
Всякое отрицательное число меньше 0.
Из двух отрицательных чисел больше то, модуль которого меньше.
Любое положительное число больше любого отрицательного числа.
Слайд 7
Проверь себя.
Даны числа: 3; 2,5; -5,6; 0,25; -
6,89, 0.
Назовите числа противоположные числам.
Найдите модуль каждого из чисел.
Выберите
число, модуль которого наибольший; наименьший.
Сравните дроби:
1) 1 и 1 ; 2) 2 и 3 ; 3) 5 и 3 .
5 8 5 4 6 8
Слайд 8
Сложение рациональных чисел
Чтобы сложить рациональные числа с одинаковыми
знаками, складывают их модули и перед суммой ставят их
общий знак.
(+19) + (+23) = 42; (-16) + (-307) = - 323.
Чтобы сложить два рациональных числа с разными знаками и разными модулями, необходимо поставить знак числа с большим модулем и приписать к нему разность между большим и меньшим модулем.
(+107) + (-56) = 51; (-23,6) + 7,5 = -16,1.
Сумма двух противоположных чисел (то есть, с разными знаками и одинаковыми модулями) равна нулю.
(-2,57) + (+2,57) = 0.
При сложении любого рационального числа и нуля получаем само это число.
Слайд 9
Законы сложения
Законы сложения положительных чисел (переместительный и сочетательный)
справедливы и для рациональных чисел. Применяя их, можно по-разному
находить сумму нескольких чисел.
Например, сложение нескольких чисел с разными знаками можно выполнять последовательно: сначала найти сумму первых двух слагаемых, к ней прибавить третье слагаемое и т. д. Но иногда удобнее сложение выполнять таким способом: сложить отдельно все положительные числа и отдельно все отрицательные числа, затем полученные два числа сложить по правилу сложения чисел с разными знаками.
(+105) + (-4) + (-8) + (+21) + (-7) = (+126) + (-19) = +107.
Слайд 10
Вычитание рациональных чисел
Вычитание рациональных чисел зависит от знаков
чисел уменьшаемого и вычитаемого.
Чтобы из одного числа вычесть
другое, достаточно к уменьшаемому прибавить число, противоположное вычитаемому.
Например: -102 — (-80) = -102 + 80 = -22.
Если уменьшаемое — отрицательное число, а вычитаемое — положительное число, то нужно сложить модули уменьшаемого и вычитаемого и перед полученным результатом поставить знак «-».
Например: -839 — 71 = — (|-839|+|-71|) = — (839+71) = -910.
Если уменьшаемое — положительное число н вычитаемое — положительное число, то нужно найти разность модулей уменьшаемого и вычитаемого и перед полученным результатом поставить знак «-», если модуль уменьшаемого меньше модуля вычитаемого. Если модуль уменьшаемого равен модулю вычитаемого, то разность равна нулю.
Примеры.
0,165 — 0,015 = 0,15 т. к. |0,1б5| > |0,0151
1 307 — 1 307 = 0 т. к. |1 307| = |1 307|
Слайд 11
умножение рациональных чисел
При умножении двух рациональных чисел умножаются

их абсолютные величины (модули чисел) и перед произведением ставится
знак, зависящий от знаков множителей.
Знак произведения определяется по таблице знаков.
Таблица знаков
Первый знак Второй знак Знак произведения
+ + +
— — +
+ — —
— + —
Если произведение содержит более двух рациональных чисел, то результат можно определить поэтапно («шаг за шагом»), на каждом этапе вычисляя произведение двух сомножителей. А можно по особому правилу определить знак произведения для всех множителей сразу.
Если в произведении все числа положительные, то модуль их произведения равен произведению модулей всех множителей, а знак произведения — «+».
Если в произведении есть числа положительные и отрицательные, то модуль их произведения равен произведению модулей всех множителей, а знак произведении «+» — при четном количестве отрицательных множителей (минусов) и «-» — при нечетном количестве отрицательных множителей (минусов).
2 — 13 * 7 * 24 = 4 368
2 * (-13) * (-7) * 24 = 4 368, т. к. количество минусов четное;
(-2) * (-13) * (-7) * 24 = -4 368, т. к. количество минусов нечетное.
Если при умножении рациональных чисел одни или несколько множителей равны 0, то все произведение равно 0.
2 * 0,71 * 172 * 0 * (176 — 176) = 0
Слайд 12
деление отрицательных чисел
Частное от деления двух отрицательных чисел
есть число положительное. Модуль частного есть частное модулей делимого
и делителя.
Например:
(-81) : (-9) = |-81|:|-9| = 81 : 9 = 9;
(-0,74) : (-0,37) = |-0.74| : |—0,37| = 0,74 : 0,37 = 2
Частное от деления отрицательного числа на положительное число и положительного числа на отрицательное число есть число отрицательное. Модуль частного есть частное модулей делимого и делителя.
Например:
(-180) : 3 = —|—180| : |3| = —(180 : 3) = -60
Рациональные числа, как и другие, па нуль делить нельзя. Если делимое нуль, а делитель — рациональное число, то при любом его значении и знаке частное равно нулю.
Правила, по которым определяется знак произведения, действительны и для частного. Поэтому знак частного тоже проверяется по таблице знаков.
Слайд 13
Степень числа
Степень любого числа — это произведение одинаковых
сомножителей. Количество сомножителей определяет показатель степени.
Четная степень отрицательного числа
— число положительное. Нечетная степень отрицательного числа — число отрицательное. Любая степень числа нуль равна нулю.