- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Презнтация по математике на тему Симметрия
Содержание
- 2. СоДеРжАнИе Истоки понятия симметприиЗеркальная симметрияЦентральная симметрияОсевая симметрияСимметрия человеческого телаСимметрияв неживой природеВиды симметрийСимметрияСимметрия в живой природеОб авторахЗаключение
- 3. Мы выбрали симметрию темой своей презентации, потому
- 4. Истоки понятия симметрии Истоки понятия
- 5. Виды симметрий Существует множество различных видов симметрии.
- 6. Зеркальная симметрия
- 7. Единственная горизонтальная симметрия, которую мы встречаем в природе,- это отражение в зеркале воды
- 8. Фигура называетсясимметричной относительно точки О,если для каждой
- 9. Симметрия относительно точки – называется центральной симметрией
- 10. Центральная симметрия присутствует там, где
- 11. Две точки А и А1 называются симметричными
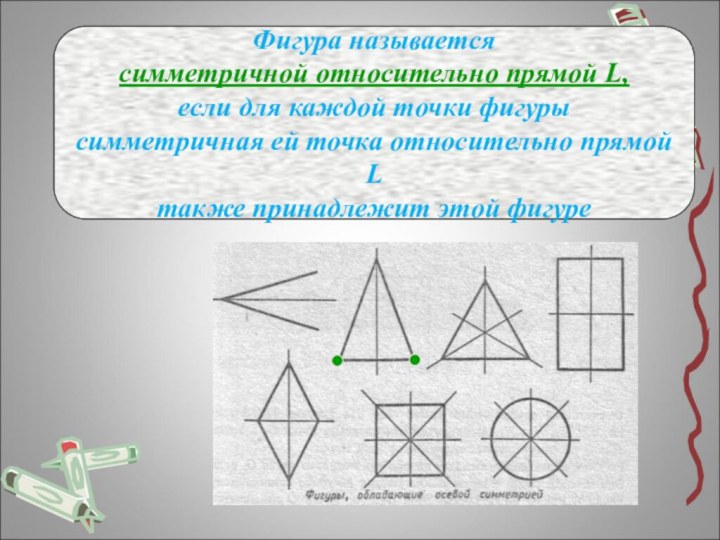
- 12. Фигура называетсясимметричной относительно прямой L,если для каждой
- 13. «Симметрия» по-гречески означает«соразмерность, пропорциональность,одинаковость расположения частей»
- 14. В архитектуре осевая симметрия используется как средство выражения архитектурного замысла
- 16. Медресе ШирдарКупол скалы в ИерусалимеИталия Рим Вывод:
- 17. Живой организм не имеет кристаллического
- 18. Симметрия, или соразмерность частей целого организма, имеет
- 19. Поворотная симметрия 5-ого порядкаЗеркальная билатеральная симметрияВывод: Симметрия ограничивает многообразие структур, которые могут существовать в природе.
- 20. Симметрия в мире растений Зеркальная симметрияПоворотная симметрия
- 21. симметрия человеческого тела Симметрия человеческого тела всегда
- 22. Человек назвался существом симметричным Существует ли на самом деле симметричный человек?
- 23. оригиналлевыеполовинкифотографииправыеполовинкифотографии
- 24. Представители класс обитателей глубин— морские черви —
- 25. Симметрия в неживой природе Вывод: Именно кристаллы вносят в мир неживой природы очарование симметрии.
- 26. Симметрия в одежде
- 28. Симметрия, проявляясь в самых различных объектах материального
- 29. Скачать презентацию
- 30. Похожие презентации
СоДеРжАнИе Истоки понятия симметприиЗеркальная симметрияЦентральная симметрияОсевая симметрияСимметрия человеческого телаСимметрияв неживой природеВиды симметрийСимметрияСимметрия в живой природеОб авторахЗаключение
























Слайд 2
СоДеРжАнИе
Истоки понятия
симметприи
Зеркальная
симметрия
Центральная
симметрия
Осевая
симметрия
Симметрия
человеческого
тела
Слайд 3 Мы выбрали симметрию темой своей презентации, потому что
она пронизывает буквально все вокруг, захватывая, казалось бы, совершенно
неожиданные области и объекты нашей жизни, но при этом, нам кажется, о ней сегодня мало говорят, считая это явление обычным, недостойным какого-либо особенного внимания.
Симметрия
Слайд 4
Истоки понятия симметрии
Истоки понятия симметрии
восходят к древним. Их наиболее важным открытием было осознание
сходства и различия правого и левого. Здесь природными образцами им служили собственное тело, а также тела животных, птиц и рыб. В качестве примера, можно вспомнить великолепные памятники архитектуры глубокой древности, где пространственные закономерности проявляются особенно ярко. Это храмы древнего Вавилона и пирамиды Гизы, дворец в Ашшуре.Итак, с глубокой древности, начиная, по-видимому, с неолита, человек постепенно осознал и пытался выразить в художественных образах тот факт, что в природе, кроме хаотического расположения одинаковых предметов или их частей, существуют некоторые пространственные закономерности. Они могут быть совсем простыми - последовательное повторение одного предмета, более сложными - повороты или отражения в зеркале. Для того чтобы точно выразить эти закономерности, нужны были специальные термины. По преданию, их придумал Пифагор Регийский.
Термином "симметрия", что в буквальном смысле значит соразмерность (пропорциональность, однородность, гармония), Пифагор Регийский обозначил пространственную закономерность в расположении одинаковых частей фигуры или самих фигур.
Слайд 5
Виды симметрий
Существует множество различных видов симметрии. К
простейшим из них относятся:
а) симметрия относительно плоскости (зеркальная симметрия);б) симметрия относительно точки (центральная симметрия);
в) симметрия относительно прямой (осевая симметрия).
Слайд 7 Единственная горизонтальная симметрия, которую мы встречаем в природе,- это отражение в
зеркале воды
Слайд 8
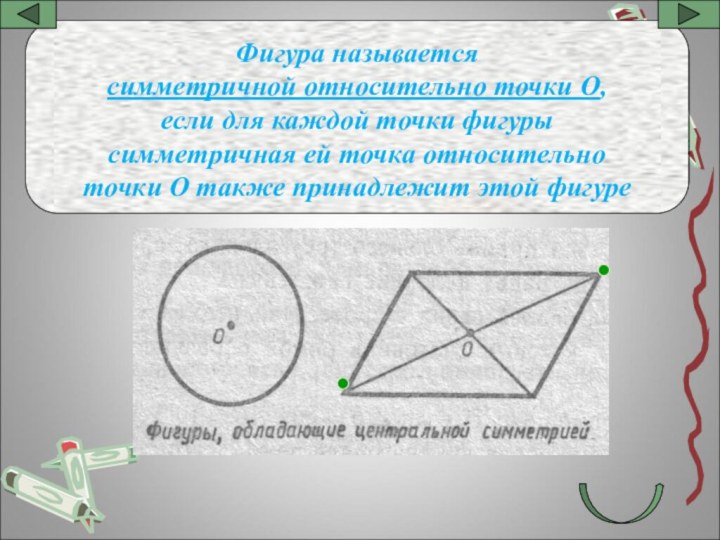
Фигура называется
симметричной относительно точки О,
если для каждой точки
фигуры
симметричная ей точка относительно
точки О также принадлежит этой фигуре
Слайд 9
Симметрия относительно точки –
называется центральной симметрией
Две
точки А и А1 называются симметричными относительно точки О,
если О – середина отрезка АА1А
А1
О
О – центр симметрии
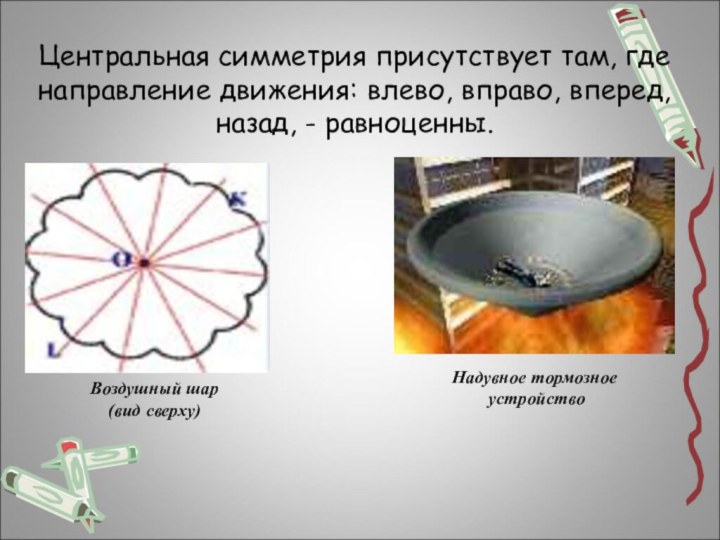
Слайд 10 Центральная симметрия присутствует там, где направление движения: влево,
вправо, вперед, назад, - равноценны.
Воздушный шар
(вид сверху)
Надувное
тормозноеустройство
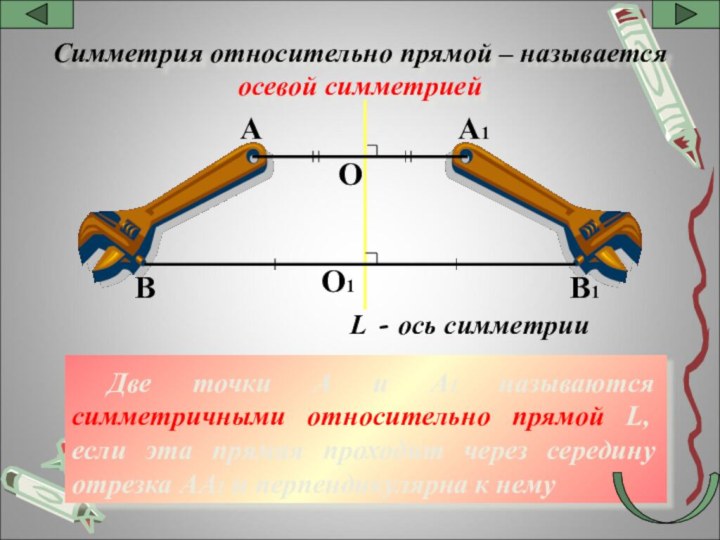
Слайд 11 Две точки А и А1 называются симметричными относительно
прямой L, если эта прямая проходит через середину отрезка
АА1 и перпендикулярна к немуВ1
А
А1
В
О
L - ось симметрии
О1
Симметрия относительно прямой – называется осевой симметрией
Слайд 12
Фигура называется
симметричной относительно прямой L,
если для каждой точки
фигуры
симметричная ей точка относительно прямой L
также принадлежит этой фигуре
Слайд 13
«Симметрия» по-гречески означает
«соразмерность, пропорциональность,
одинаковость расположения частей»
Слайд 16
Медресе Ширдар
Купол скалы в Иерусалиме
Италия Рим
Вывод: когда
мы говорим о гармонии, красоте, эмоциональности, мы тем самым
касаемся симметрии.Слайд 17 Живой организм не имеет кристаллического строения
в том смысле, что даже отдельные его органы не
обладают пространственной решеткой.Однако упорядоченные структуры в ней представлены очень широко. Если они жидкие, то их называют жидкими кристаллами. В этих структурах сильно вытянутые молекулы расположены так, что их длинные оси в среднем ориентированы в одну сторону. В некоторых случаях образуются дополнительные сверхструктуры: возникает закручивание или слоистые структуры.
Жидкие кристаллы, как и твердые, обладают анизотропией физических свойств. Однако пространственной решетки жидкие кристаллы не имеют.
Слайд 18 Симметрия, или соразмерность частей целого организма, имеет непосредственное
отношение к характеру приспособленности животных к условиям существования
Слайд 19
Поворотная симметрия 5-ого порядка
Зеркальная билатеральная симметрия
Вывод: Симметрия ограничивает
многообразие структур, которые могут существовать в природе.
Слайд 21
симметрия человеческого тела
Симметрия человеческого тела всегда являлась
и является основным источником нашего эстетического восхищения хорошо сложенным
человеческим телом.
Слайд 24
Представители класс обитателей глубин— морские черви — имеют
цилиндрическое тело, а в ротовой полости — массу острых
зубов. Зубы расположены так, что если соединить их прямыми линиями, то получится пятиугольник. Такой феномен Никлз объясняет следующим образом. Если бы число зубов было четным, то они мешали бы друг другу. Минимальное нечетное число — три, но треугольник сильно отличается от круга и не соответствует цилиндрическому телу червя. Семь, девять и больше зубов — излишняя роскошь, которую природа не может себе позволить. Поэтому реализуется оптимальный случай, наиболее соответствующий круговому сечению ротового отверстия, пятиугольник.Если рассматривать царство живого, то любому его представителю, от простейшей водоросли до эвкалипта, от крошечного жучка до кита, от червяка до человека, можно приписать одну из групп симметрии (точечных или пространственных), выведенных для материальных фигур..
Слайд 25
Симметрия в неживой природе
Вывод: Именно кристаллы вносят
в мир неживой природы очарование симметрии.
Слайд 28 Симметрия, проявляясь в самых различных объектах материального мира,
несомненно, отражает наиболее общие, наиболее фундаментальные его свойства. Поэтому
исследование симметрии разнообразных природных объектов и сопоставление его результатов является удобным и надежным инструментом познания основных закономерностей существования материи.Можно надеяться, что на основе биологических законов сохранения, разнообразных инвариантов, симметрии законов живой природы относительно тех или иных преобразований рано или поздно удастся глубже проникнуть в сущность живого, объяснить ход эволюции, её вершины, тупики, предсказать неизвестные сейчас ветви, теоретически возможные и действительные числа типов, классов, семейств…организмов. И вообще нужно проанализировать вопрос о том, нельзя ли эволюцию материи в целом и внутри отдельных её форм представить как групповые преобразования, найти их инварианты и на основе последних определить все возможные варианты эволюции в цело и в частностях, предсказать возможные её ветви – число, характер и т. д. Таким образом, развитый здесь подход даёт возможность поставить вопрос о неединственности той картины развития, которую мы знаем.
Заключение...





























