может принимать аргумент, т.е. множество значений х, для которых
можно вычислить у, если функция задана формулой.Обозначение:
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Построение графиков функций с использованием производной
Содержание
- 2. Основные понятия
- 3. 1. Область определения функции-множество всех
- 4. 2. Область изменения функцииили множество значений функции. Обозначение:
- 5. 3. Точки пересечения с осями координат.Ордината точки
- 6. 4. Четные, нечетные функции и функции общего
- 7. Область определения нечетной функции-интервал оси Ох, симметричный
- 8. 5. Периодические функции. -периодическая
- 9. 6. Ограниченные функции.
- 10. 7. Точки разрыва функции и их характер.Для
- 11. Виды точек разрыва: -точка устранимого разрыва
- 12. -точка конечного разрываАВх0
- 13. -точка бесконечного разрыва
- 14. 8. Асимптоты графика функций.Прямая l называется асимптотой
- 16. Виды асимптотВертикальнаяГоризонтальнаяНаклоннаяЕсли f(x) можно представить в виде
- 17. 9.Возрастание и убывание функции на интервале
- 19. Достаточные признаки возрастания и убывания функции: ЕслиЕсли
- 20. 10.Точки экстремумаВ окрестности точки х0, f(х0)-наименьшеезначение функции
- 21. Достаточные признаки точки экстремума.
- 22. 1ый достаточный признак Точка х0 –точка максимума
- 24. 2ой достаточный признак
- 25. 11.Выпуклость и вогнутость
- 26. Достаточные признаки выпуклости и вогнутости Кривая вогнута на (a;b)
- 27. 12.Точки перегиба функцииухf(х0)х0
- 28. Достаточный признак точки перегиба Для построения точки
- 29. Связь между существованием производной в точке х0
- 30. Различные типы точек перегиба:х0х0х0х0х0х0х0х0
- 31. Скачать презентацию
- 32. Похожие презентации
Основные понятия
Слайд 5
3. Точки пересечения с осями координат.
Ордината точки пересечения
с осью Оу находится из условия
у= f(0)
Абсциссы точек пересечения
с осью Ох (нули функции) находятся из условия f(x) =0.
Слайд 6
4. Четные, нечетные функции и функции общего положения.
Область
определения четной функции- интервал оси Ох, симметричный относительно точки
О.График четной функции симметричен относительно оси Оу.
Слайд 7 Область определения нечетной функции-интервал оси Ох, симметричный относительно
точки О.
График нечетной функции симметричен относительно начала координат.
Функция, не являющаяся ни нечетной, ни четной, называется функцией общего положения.
Слайд 10
7. Точки разрыва функции и их характер.
Для элементарных
функций точка разрыва - это такая точка, в которой
функция не определена, но определена в окрестностях этой точки.
Слайд 14
8. Асимптоты графика функций.
Прямая l называется асимптотой
графика
функции у=f(x), если
расстояние от точки М графика до
прямой стремится
к нулю приудалении точки М до кривой в
бесконечность.
Слайд 16
Виды асимптот
Вертикальная
Горизонтальная
Наклонная
Если f(x) можно представить в виде f(x)=kx+b+
, где
, когда , то прямая y=kx+b является асимптотой:
при k равном нулю - горизонтальной,
при k не равном нулю- наклонной.
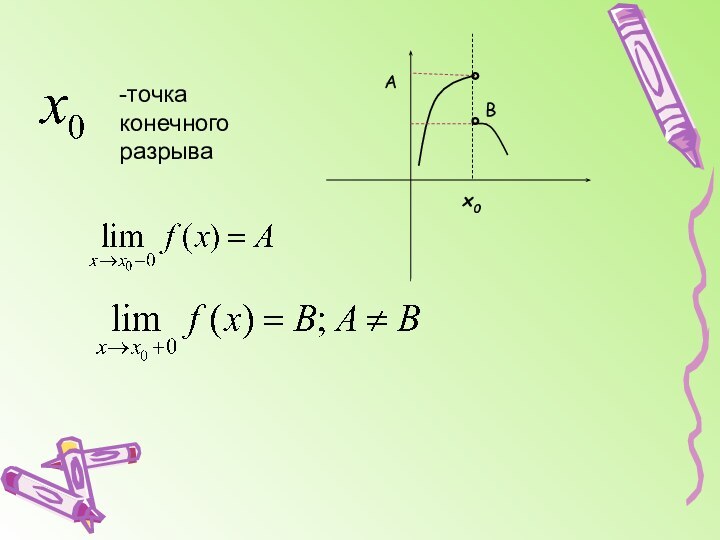
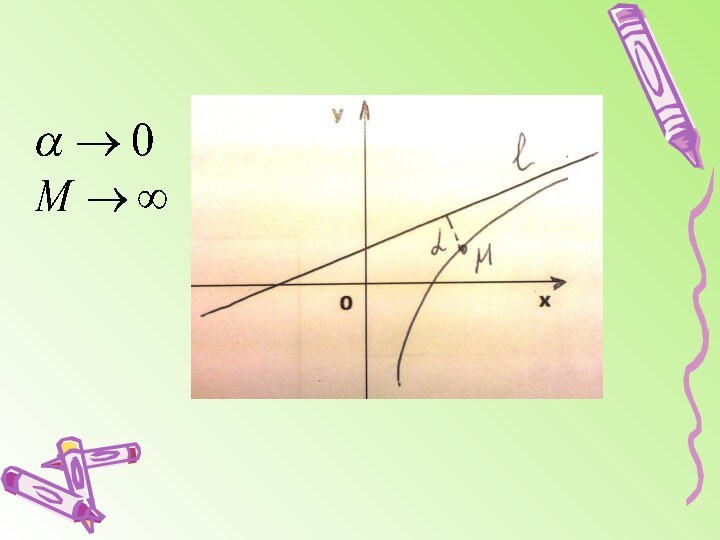
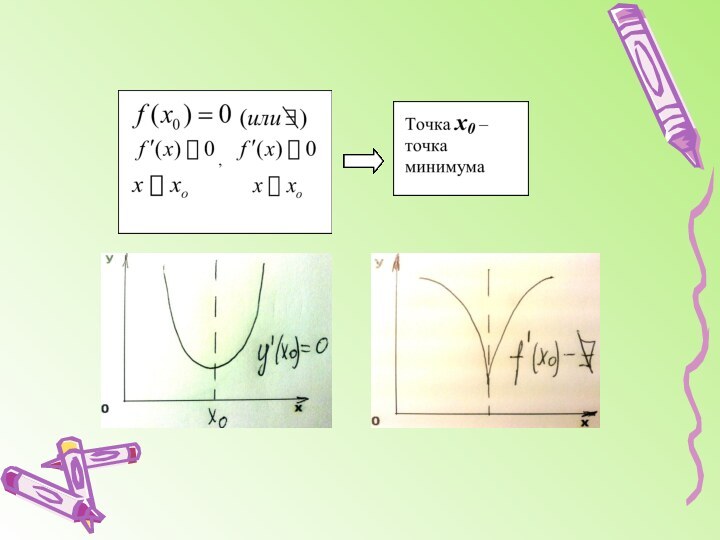
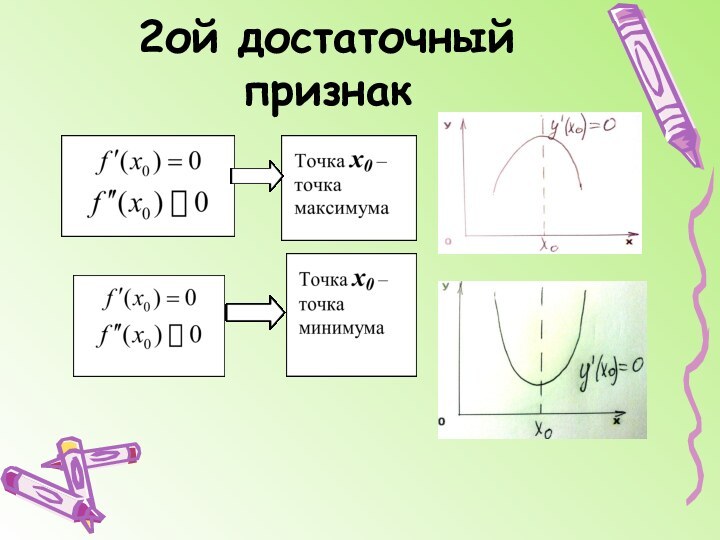
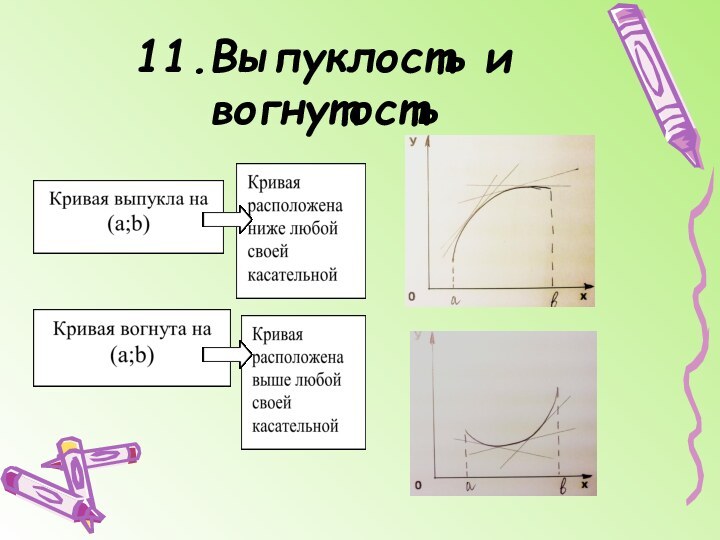
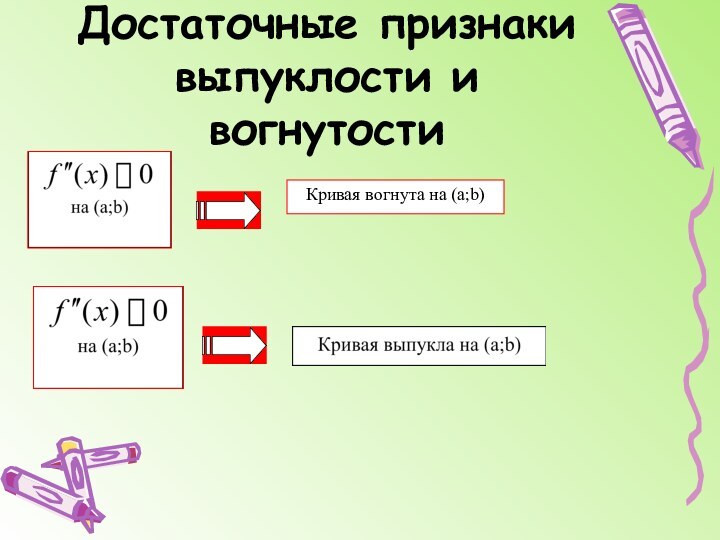
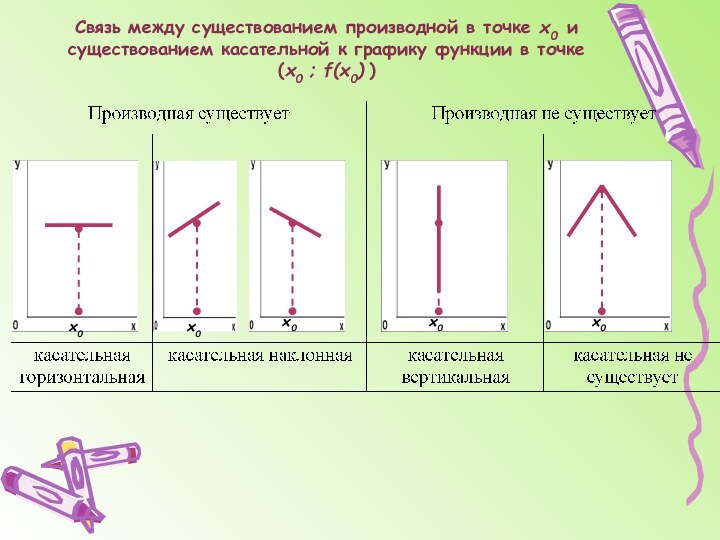
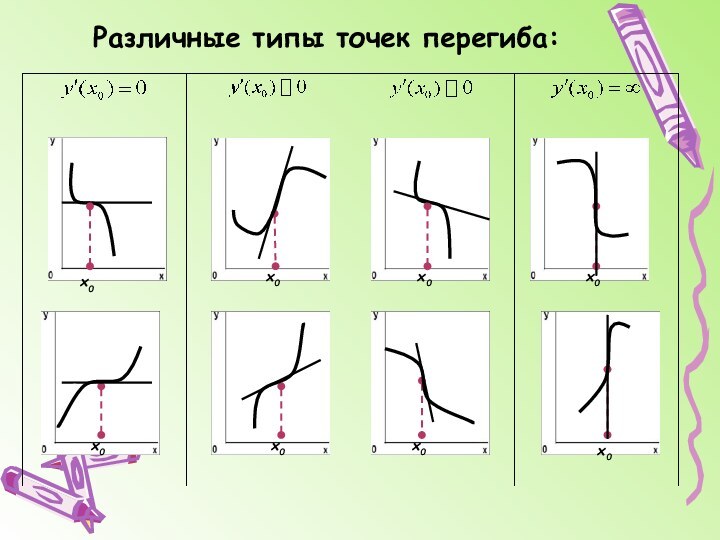
График функции может иметь вертикальные асимптоты в точках разрыва (бесконечного) или на границах области определения функции.
Слайд 28
Достаточный признак точки перегиба
Для построения точки перегиба необходимо
установить связь между существованием производной в точке х0 и
существованием касательной к графику функции в точке (х0 ; f(х0) ).Слайд 29 Связь между существованием производной в точке х0 и
существованием касательной к графику функции в точке (х0 ;
f(х0) )х0
х0
х0
х0
х0
