- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Построение касательной к окружности
Содержание
- 2. ПовторениеРасстояние между двумя точками-длина отрезка, соединяющего эти
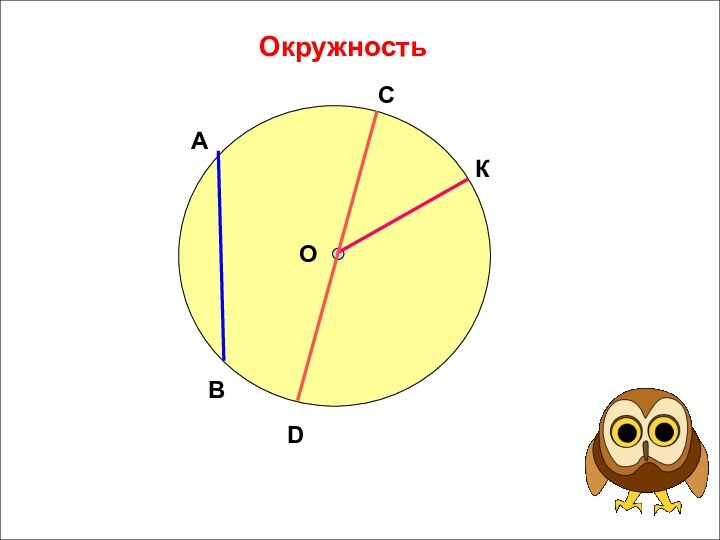
- 3. ОкружностьАВСDОК
- 4. В окружности с центром в точке О
- 5. В окружности с центром в точке О
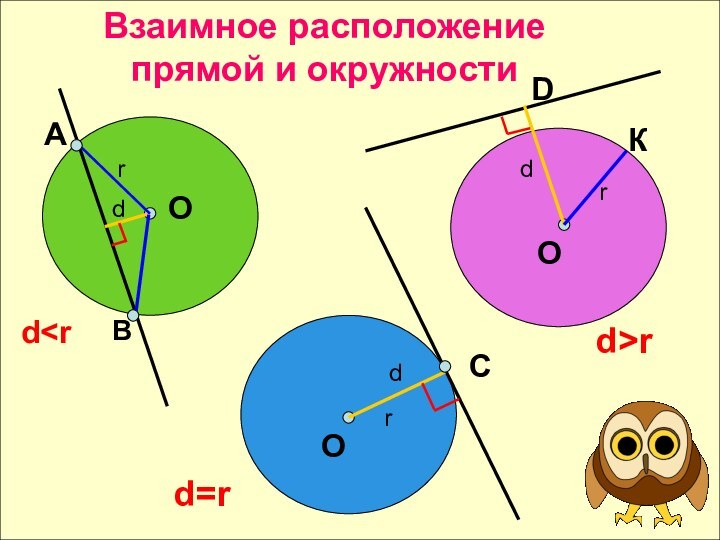
- 6. Взаимное расположение прямой и окружностиАВrddrСОООКD
- 7. Среди следующих утверждений укажите истинные.Окружность и прямая
- 8. Закончите фразу, чтобы получилось верное высказывание:Окружность и
- 9. Установите истинность или ложность утверждений:Прямая а является
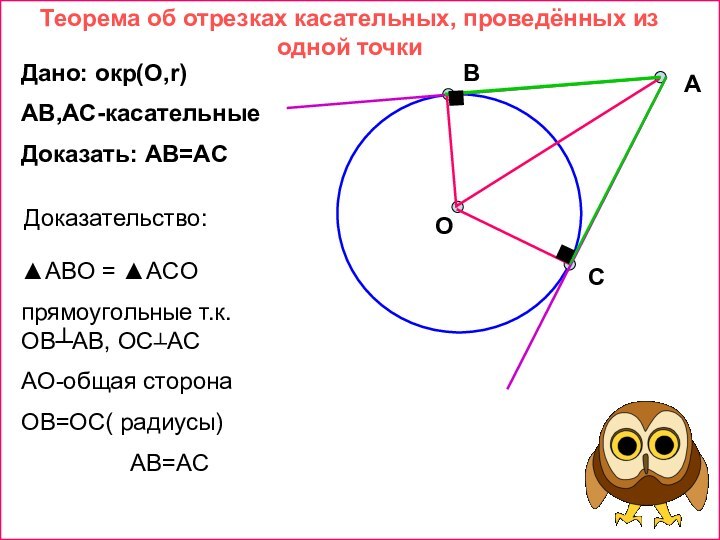
- 10. Теорема об отрезках касательных, проведённых из одной
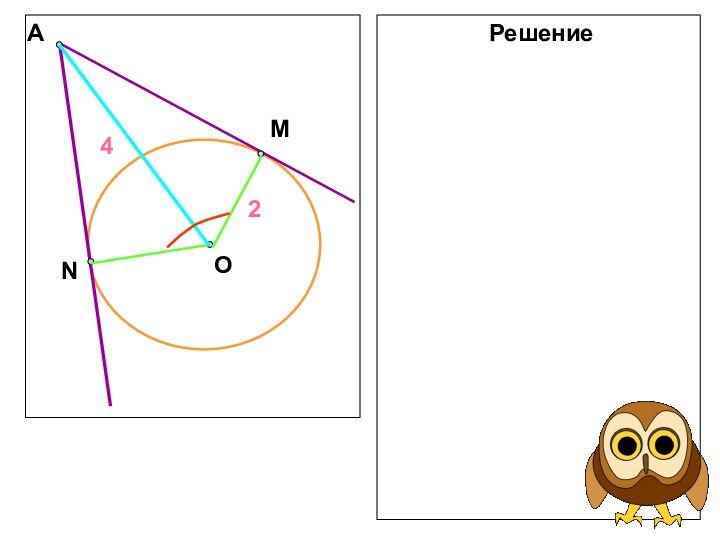
- 11. АСОВРешение:Решение
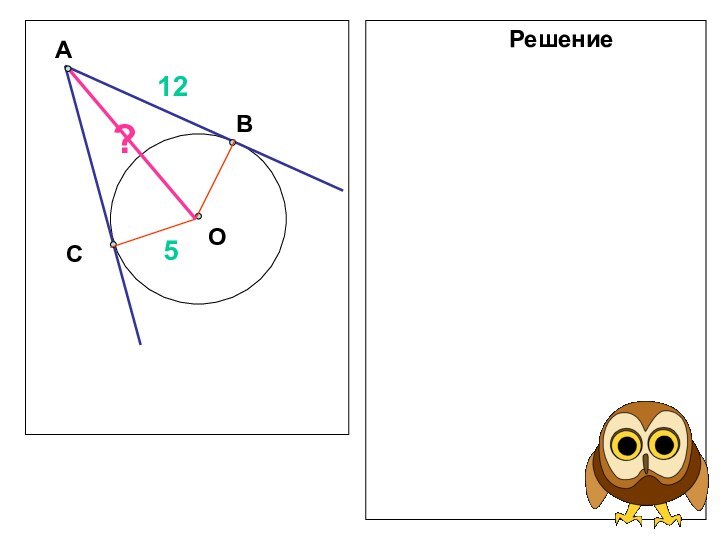
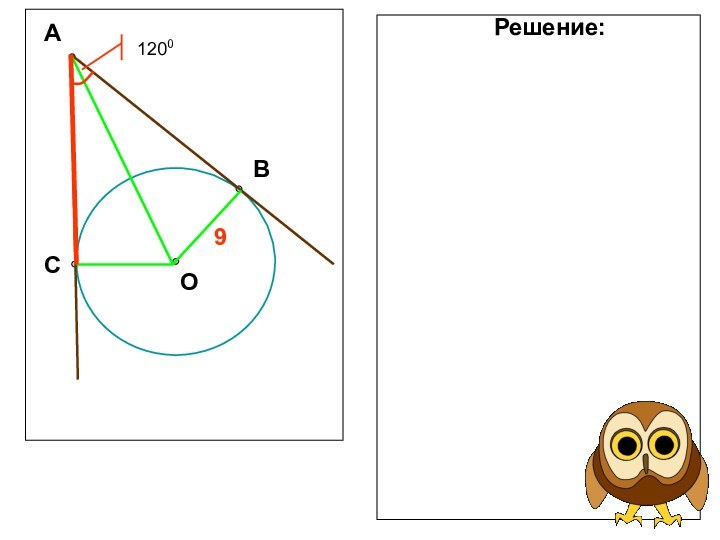
- 12. ОСВА9Решение:
- 13. Скачать презентацию
- 14. Похожие презентации
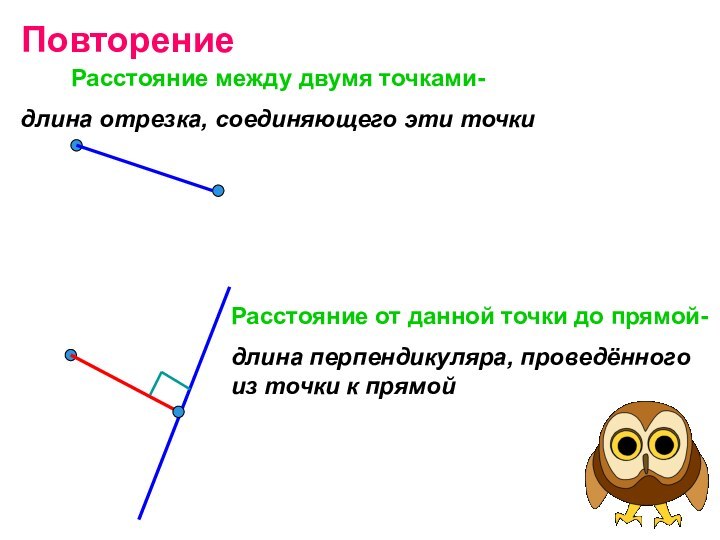
ПовторениеРасстояние между двумя точками-длина отрезка, соединяющего эти точкиРасстояние от данной точки до прямой-длина перпендикуляра, проведённого из точки к прямой




Слайд 2
Повторение
Расстояние между двумя точками-
длина отрезка, соединяющего эти точки
Расстояние
от данной точки до прямой-
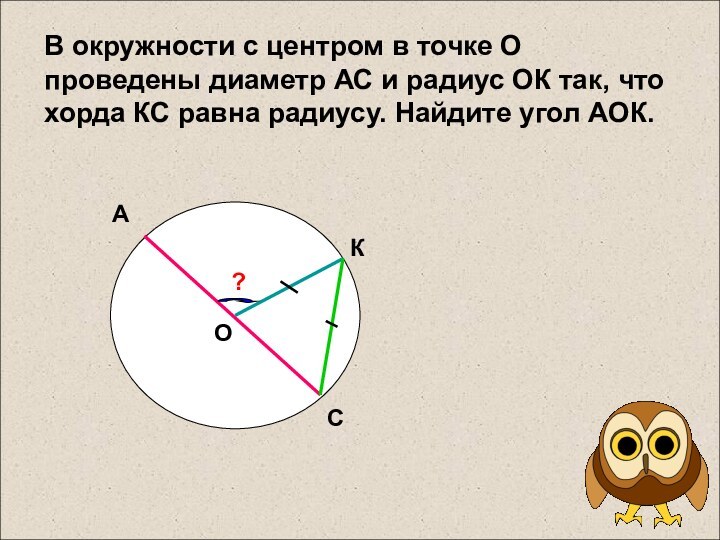
к прямойСлайд 4 В окружности с центром в точке О проведены
диаметр АС и радиус ОК так, что хорда КС
равна радиусу. Найдите угол АОК.А
С
О
К
?
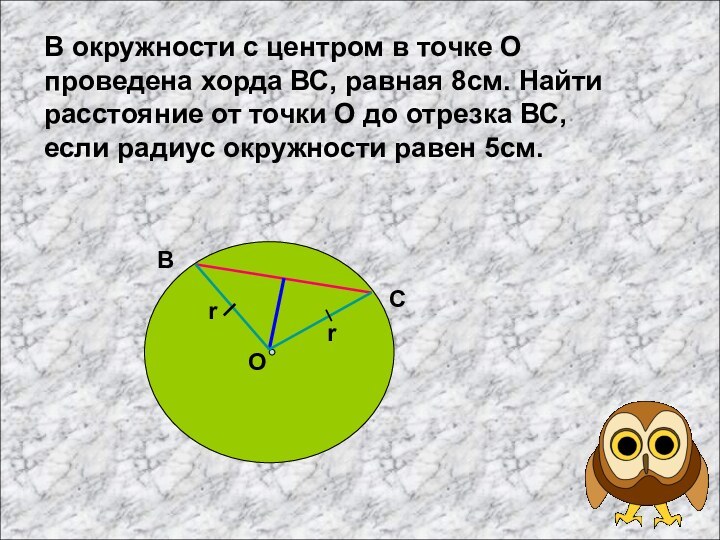
Слайд 5 В окружности с центром в точке О проведена
хорда ВС, равная 8см. Найти расстояние от точки О
до отрезка ВС, если радиус окружности равен 5см.В
С
О
r
r
Слайд 7
Среди следующих утверждений укажите истинные.
Окружность и прямая имеют
две общие точки, если:
Расстояние от центра окружности до прямой
не превосходит радиуса окружности;расстояние от центра окружности до прямой меньше радиуса окружности;
расстояние от окружности до прямой меньше радиуса.
Слайд 8
Закончите фразу, чтобы получилось верное высказывание:
Окружность и прямая
имеют одну общую точку, если …
Вставьте пропущенные слова.
Окружность и
прямая имеют одну общую точку, если … расстояние от … до прямой…
Слайд 9
Установите истинность или ложность утверждений:
Прямая а является секущей
по отношению к окружности, если она имеет с окружностью
общие точки.Прямая а является секущей по отношению к окружности, если она пересекает окружность в двух точках.
Прямая а является секущей по отношению к окружности, если расстояние от центра окружности до данной прямой не больше радиуса.