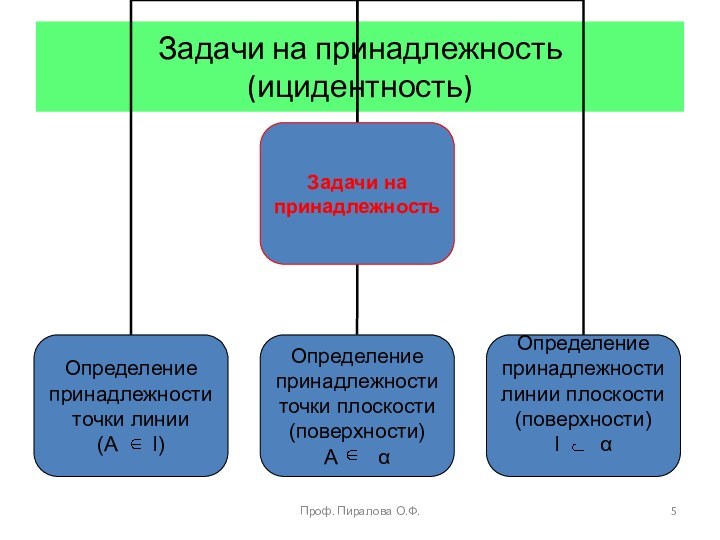
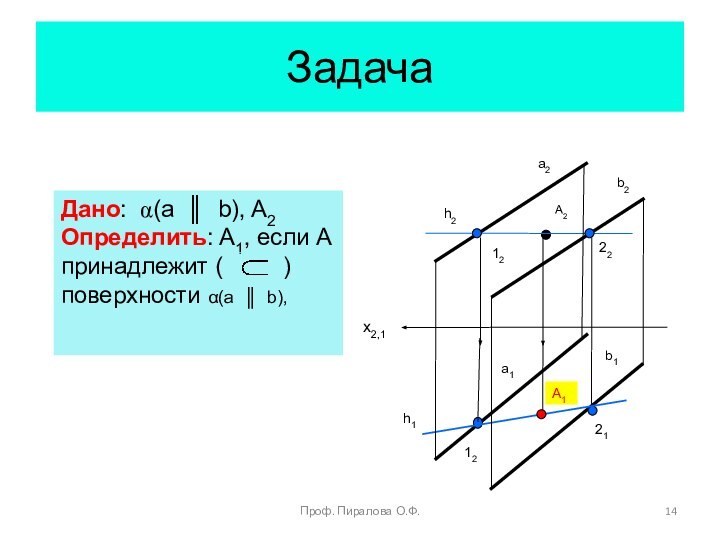
точки плоскости
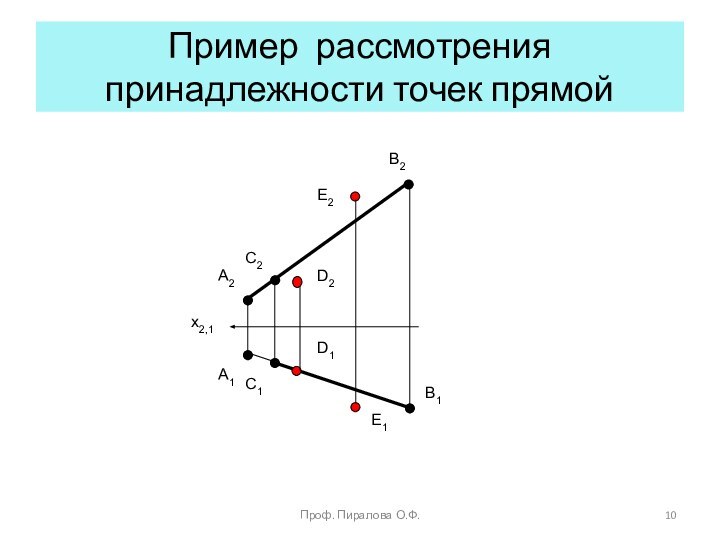
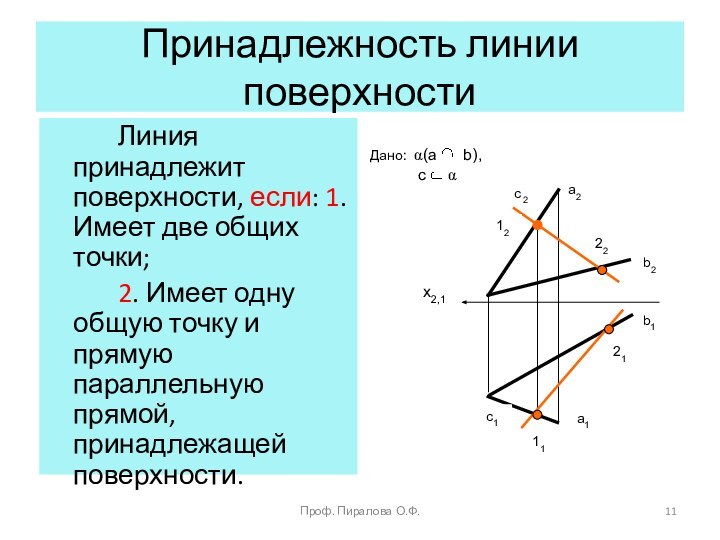
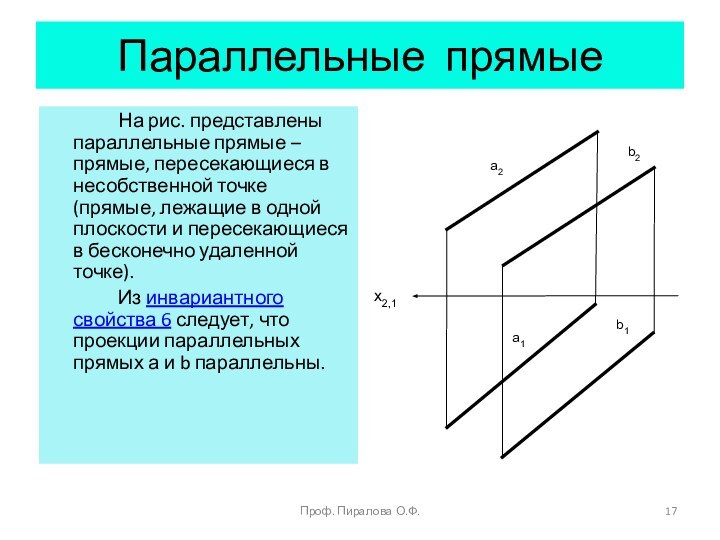
Принадлежность линии плоскости
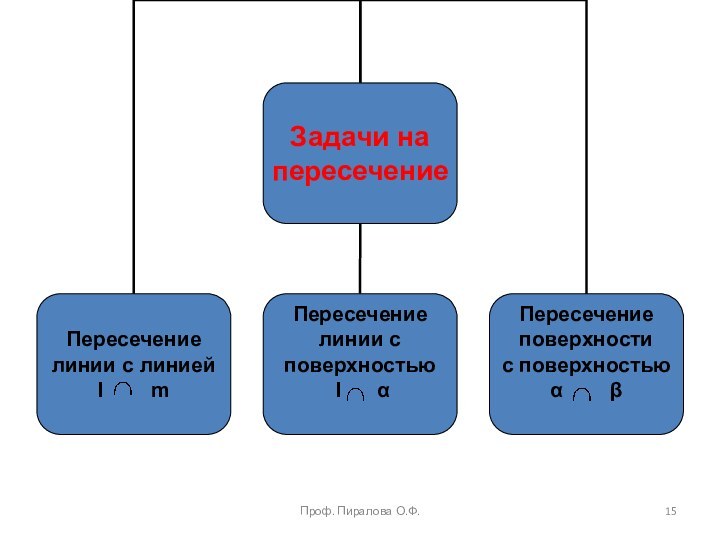
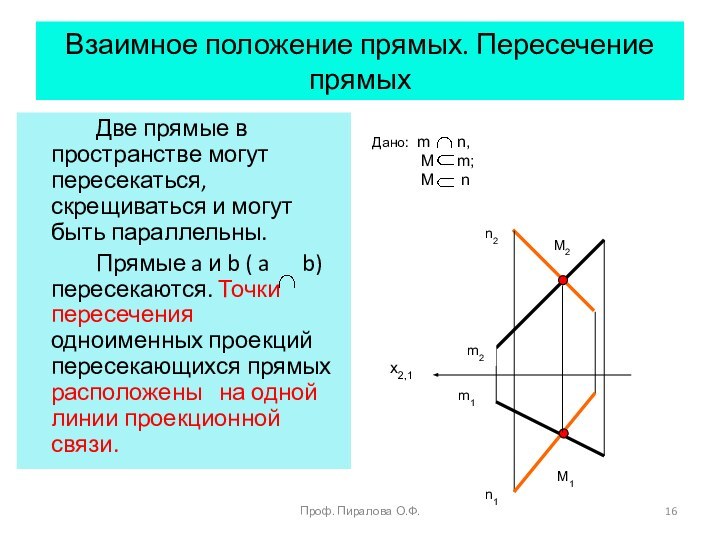
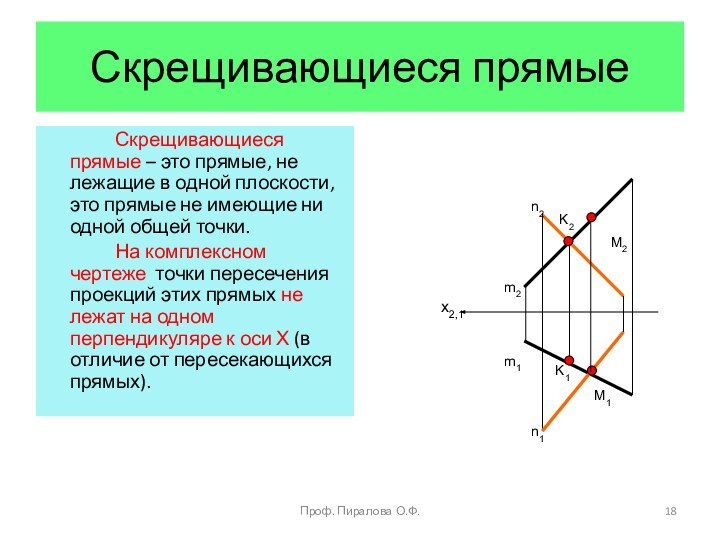
Пересечение линии линией
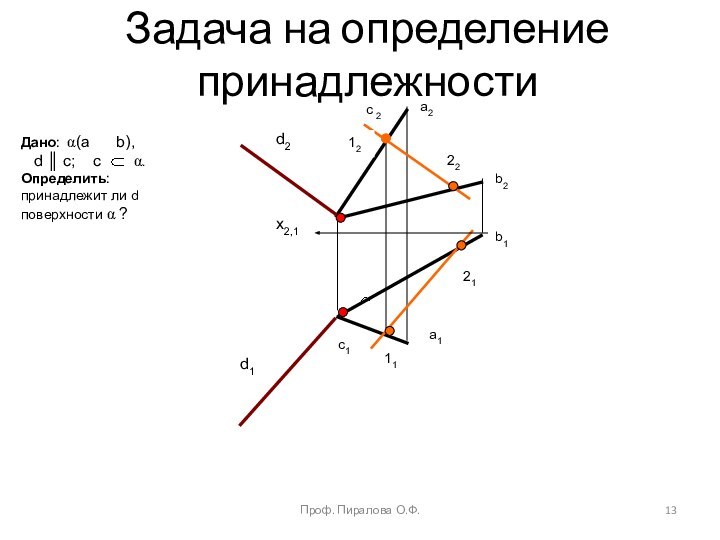
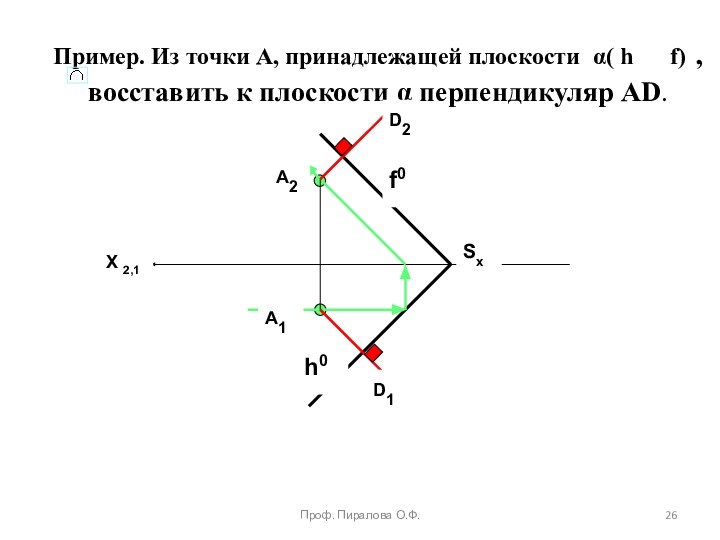
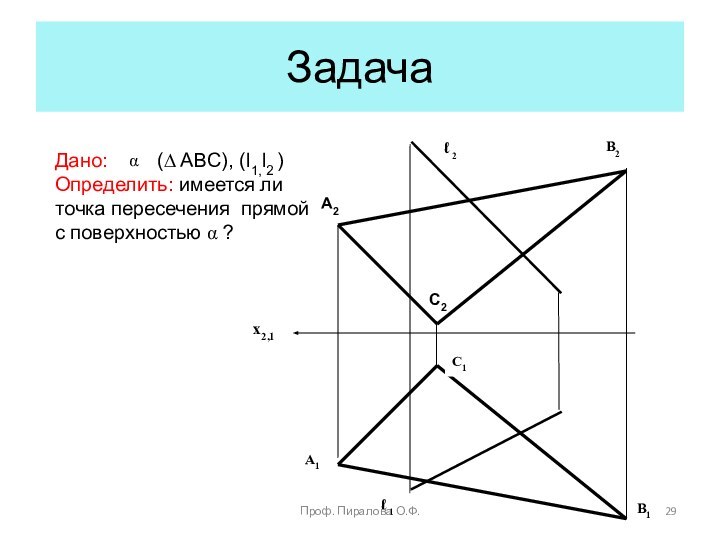
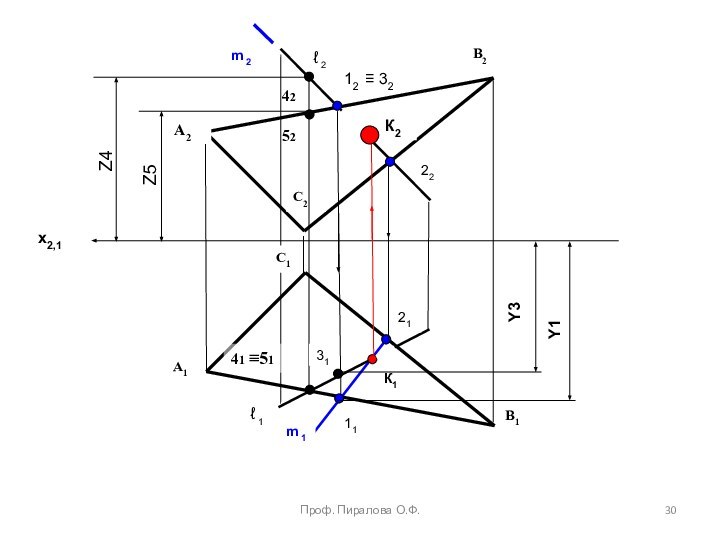
Пересечение линии с плоскостью
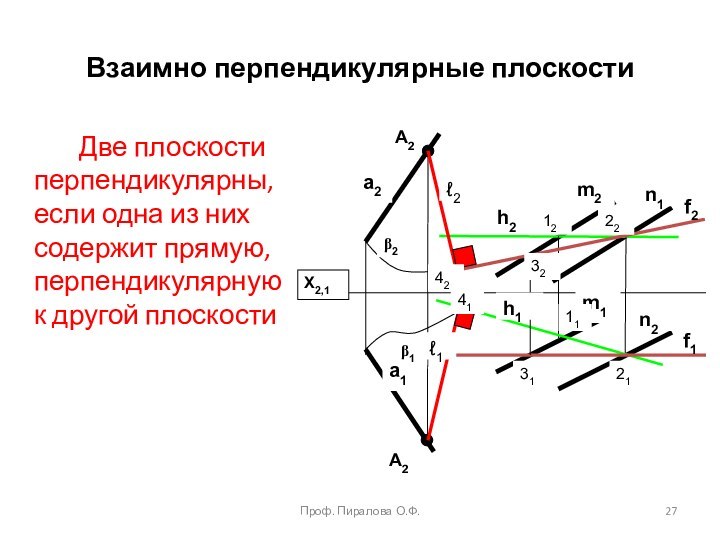
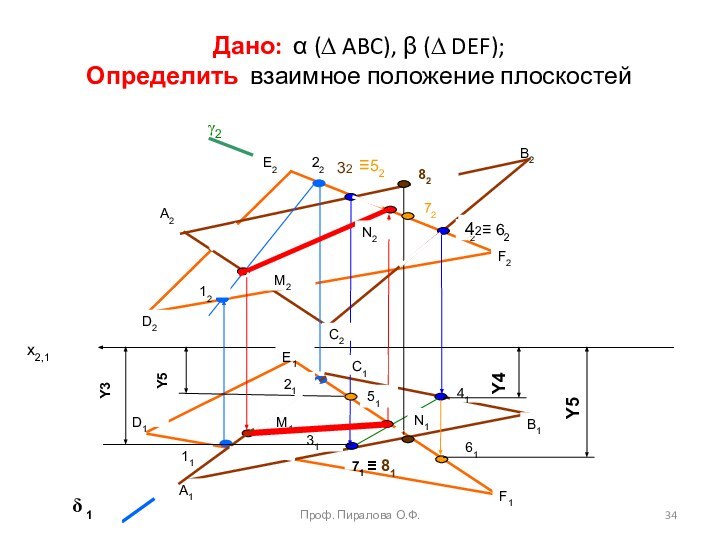
Взаимное
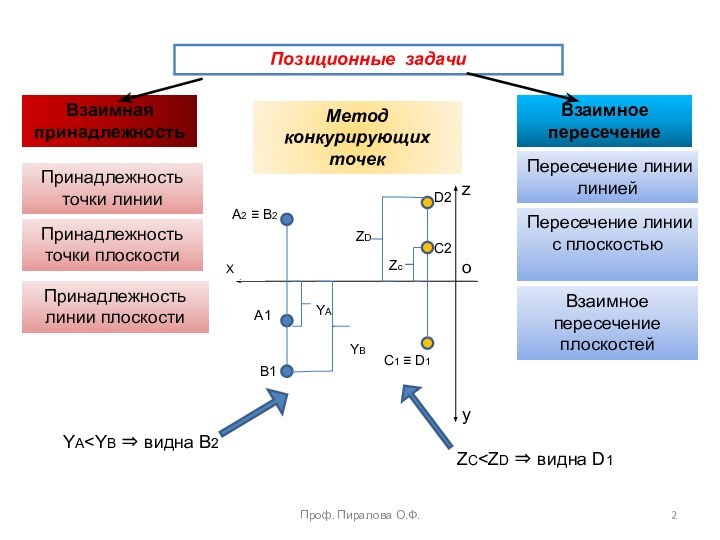
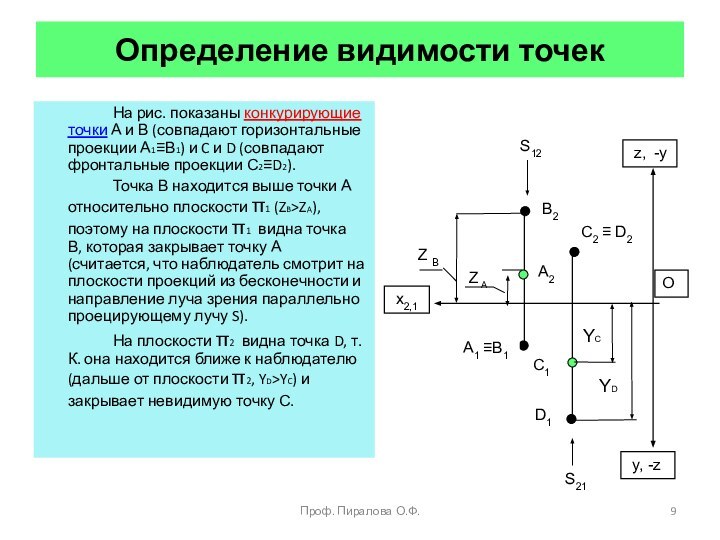
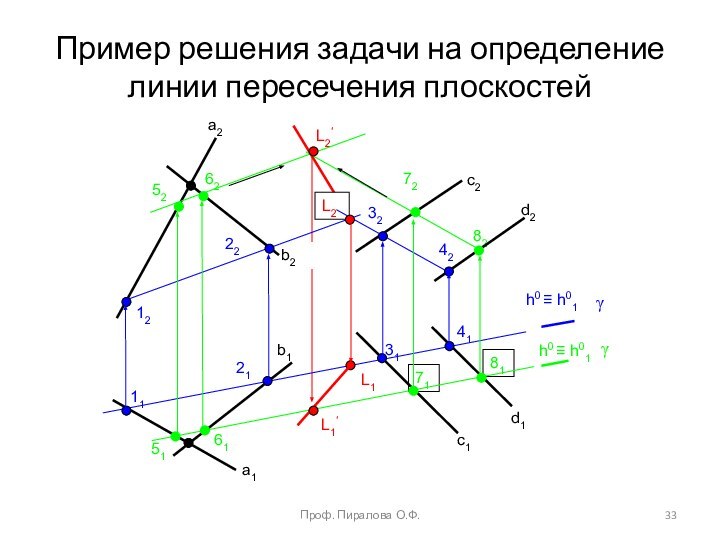
пересечение плоскостейМетод конкурирующих точек
Х
z
o
y
A2 ≡ B2
A1
B1
YA
YB
YA С1 ≡ D1 C2 D2 Zc ZD ZC