- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Практическое применение логарифмов в экономике
Содержание
- 2. Непер Джон(1550 - 1617)Известный английский математик, шотландский
- 3. Можно найти применение логарифмам не только в
- 4. Пример 1. Задача о вкладчике.Пусть вкладчик положил
- 5. Попробуем найти закон образования суммы вклада после каждого годаПосле первого годаПосле второго года
- 6. Через n лет хранения денег их количество составитВывели формулу, которая в экономике называется формулой сложных процентов
- 7. В нашем случае деньги на вкладе накапливаются
- 8. Рассмотрим этот же пример в общем видеНекоторая
- 9. Пример. Пенсионер 1 января положил на вклад
- 10. В итоге получим, что закон образования суммы
- 12. Скачать презентацию
- 13. Похожие презентации
Непер Джон(1550 - 1617)Известный английский математик, шотландский барон. Математика и астрономия были его увлечениями, а не профессией. Непер вошел в историю математики как изобретатель логарифмов, составитель первой таблицы логарифмов, которой он посвятил 20 лет своей жизни.











Слайд 3 Можно найти применение логарифмам не только в математике,
но и в других областях науки, например, экономике, в
частности, в банковском деле
Слайд 4
Пример 1. Задача о вкладчике.
Пусть вкладчик положил в
банк 10 000 рублей под ставку 12 % годовых.
Через сколько лет его вклад удвоится?Через год на счету вкладчика будет сумма:
Еще через год эта сумма составит
Слайд 5 Попробуем найти закон образования суммы вклада после каждого
года
После первого года
После второго года
Слайд 6
Через n лет хранения денег их количество составит
Вывели
формулу, которая в экономике называется формулой сложных процентов
Слайд 7 В нашем случае деньги на вкладе накапливаются по
формуле
Нам необходимо найти n, при котором
т.е. решить уравнение
по
определению логарифма получимУвеличение вклада произойдет через 6 лет (с небольшим)
Слайд 8
Рассмотрим этот же пример в общем виде
Некоторая сумма
денег в А рублей подвержена приросту в р% годовых.
Через сколько лет эта сумма составит S рублей?Прологарифмируем это уравнение по основанию 10, получим:
Слайд 9
Пример.
Пенсионер 1 января положил на вклад все
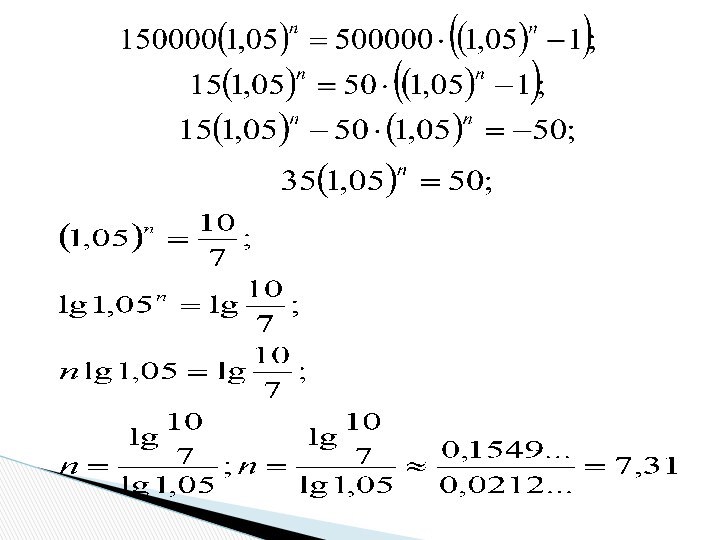
свои сбережения – 150 000 рублей под 5% годовых.
Он намеревается каждый год 31 декабря снимать с вклада по 25 тыс.рублей. На протяжении какого периода времени он это может делать?Рассмотрим ситуацию в общем виде. Пусть А – исходная сумма, S – снимаемая сумма ежегодно, Р – процентная ставка.
Тогда через год на счету будет
а после снятия денег
через два года
Слайд 10 В итоге получим, что закон образования суммы в
конце каждого года после съема денег с вклада
Для нашего
случая получим:Нам надо найти, при каком значении n эта сумма будет равна нулю.





























