- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Правильная пирамида
Содержание
- 2. Цели урока: введение понятия правильной пирамиды;рассмотрение свойств
- 3. Ответить на вопросыСформулируйте определение пирамиды. Покажите на
- 4. Проверка домашнего задания.№ 247 аДвугранные углы при
- 5. Прверка домашнего задания.№ 249 аОРА1А2АnВ пирамиде все
- 6. Правильные многоугольники.ОВ правильном многоугольникецентры вписанной и описанной
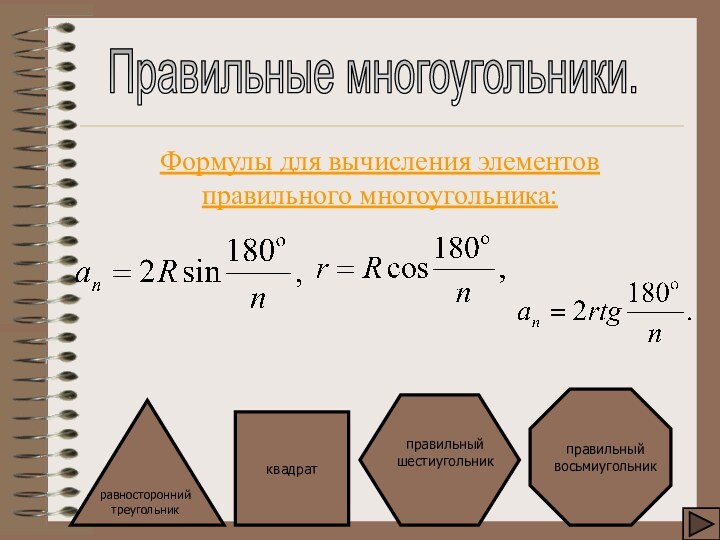
- 7. Правильные многоугольники.Формулы для вычисления элементов правильного многоугольника:
- 8. Тема урока: "Правильная пирамида".Пирамида – правильная, если1)
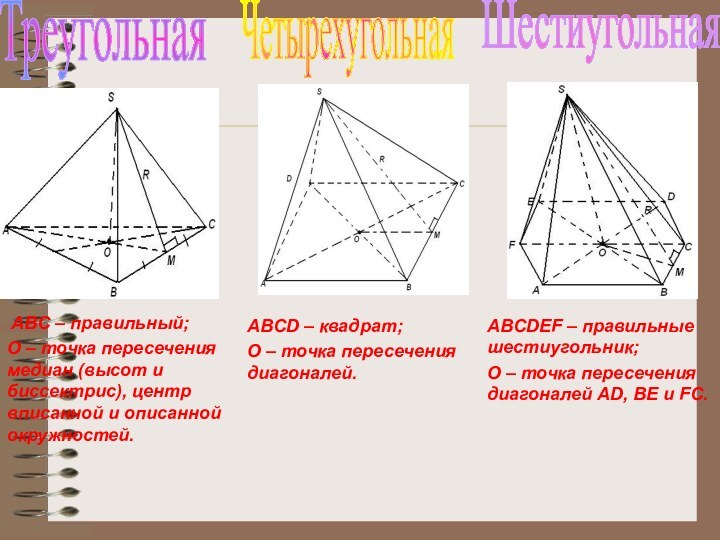
- 9. ТреугольнаяЧетырехугольнаяШестиугольная
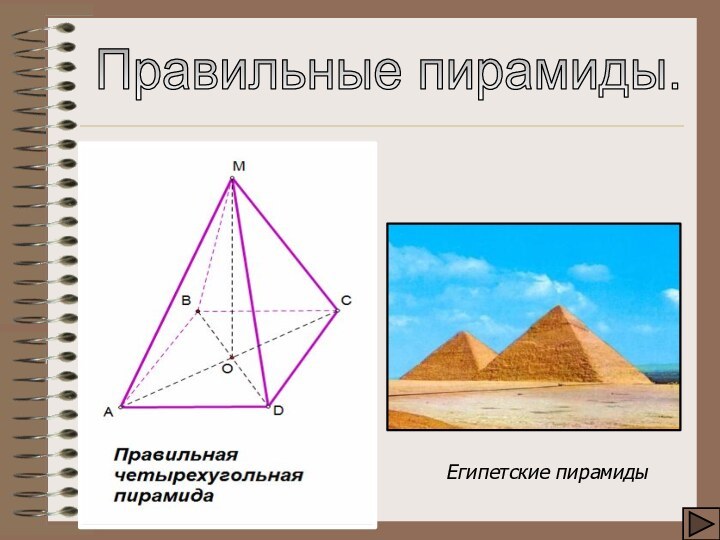
- 10. Египетские пирамидыПравильные пирамиды.
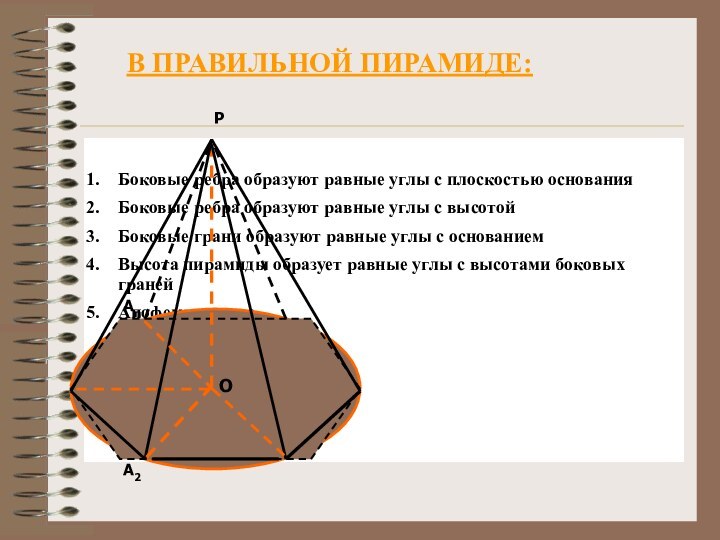
- 11. В правильной пирамиде: Боковые ребра
- 12. Апофема.МН - апофемаАпофема – высота боковой грани
- 13. В правильной четырехугольной пирамиде
- 14. Дано: MAВCD – правильная пирамида. Построить: (AM
- 15. Дано: MAВCD – правильная пирамида. Построить: (CMD
- 16. Дано: MAВCD – правильная пирамида. Построить: (AВM
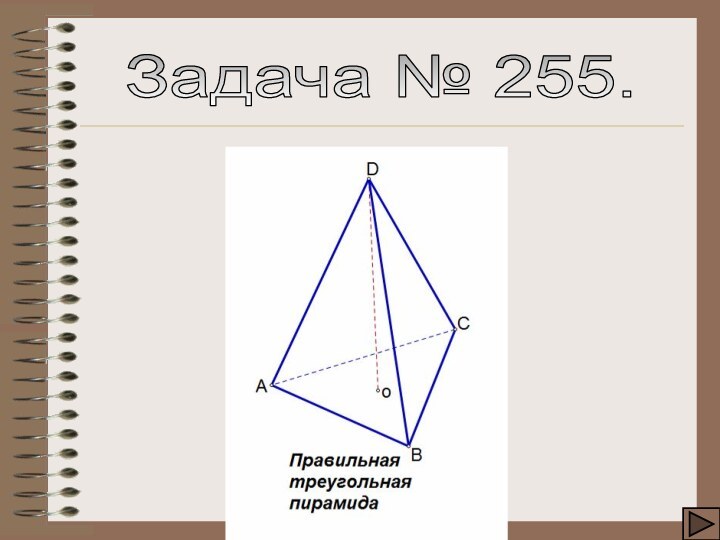
- 17. Задача № 255.
- 18. Итоги урока.Какая пирамида называется правильной? Являются ли
- 19. Скачать презентацию
- 20. Похожие презентации
Цели урока: введение понятия правильной пирамиды;рассмотрение свойств правильной пирамиды;введение понятия апофема;рассмотрение задач на нахождение элементов правильной пирамиды



Слайд 3
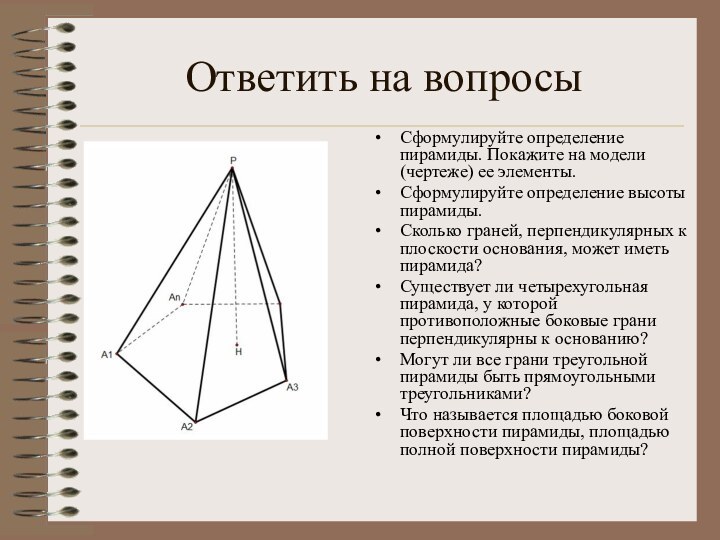
Ответить на вопросы
Сформулируйте определение пирамиды. Покажите на модели
(чертеже) ее элементы.
Сформулируйте определение высоты пирамиды.
Сколько граней, перпендикулярных
к плоскости основания, может иметь пирамида?Существует ли четырехугольная пирамида, у которой противоположные боковые грани перпендикулярны к основанию?
Могут ли все грани треугольной пирамиды быть прямоугольными треугольниками?
Что называется площадью боковой поверхности пирамиды, площадью полной поверхности пирамиды?
Слайд 4
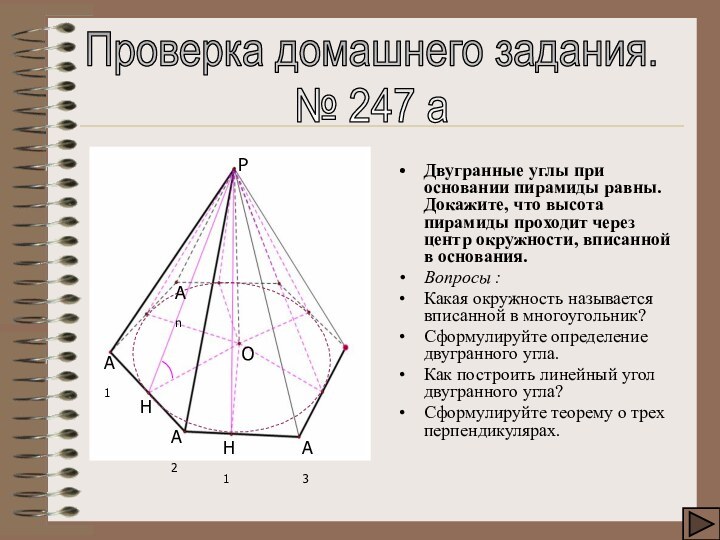
Проверка домашнего задания.
№ 247 а
Двугранные углы при основании
пирамиды равны. Докажите, что высота пирамиды проходит через центр
окружности, вписанной в основания.Вопросы :
Какая окружность называется вписанной в многоугольник?
Сформулируйте определение двугранного угла.
Как построить линейный угол двугранного угла?
Сформулируйте теорему о трех перпендикулярах.
Слайд 5
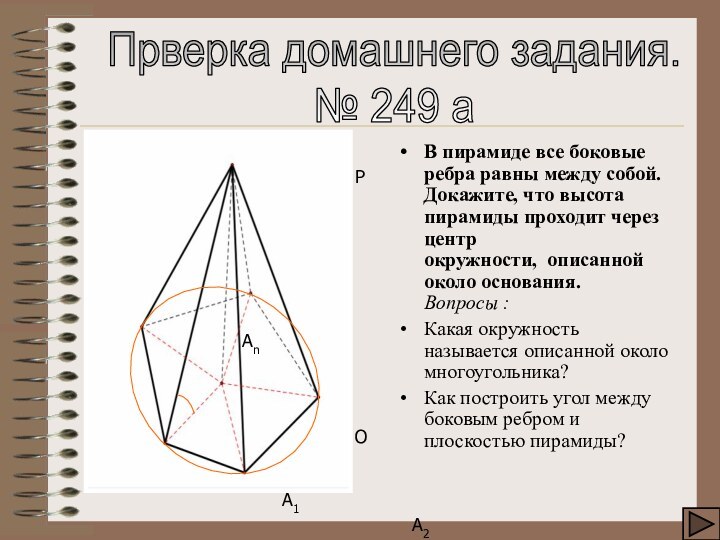
Прверка домашнего задания.
№ 249 а
О
Р
А1
А2
Аn
В пирамиде все боковые
ребра равны между собой. Докажите, что высота пирамиды проходит
через центр окружности, описанной около основания. Вопросы :Какая окружность называется описанной около многоугольника?
Как построить угол между боковым ребром и плоскостью пирамиды?
Слайд 6
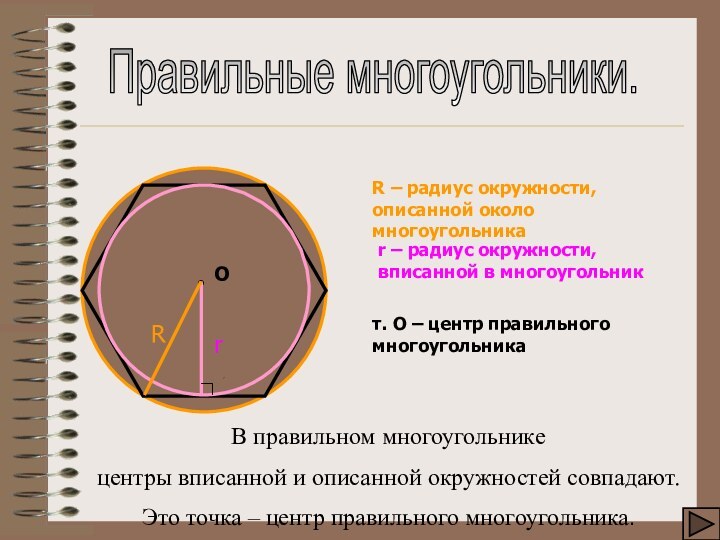
Правильные многоугольники.
О
В правильном многоугольнике
центры вписанной и описанной окружностей
совпадают. Это точка – центр правильного многоугольника.
r
R
R – радиус
окружности, описанной около многоугольникат. О – центр правильного многоугольника
r – радиус окружности, вписанной в многоугольник
Слайд 8
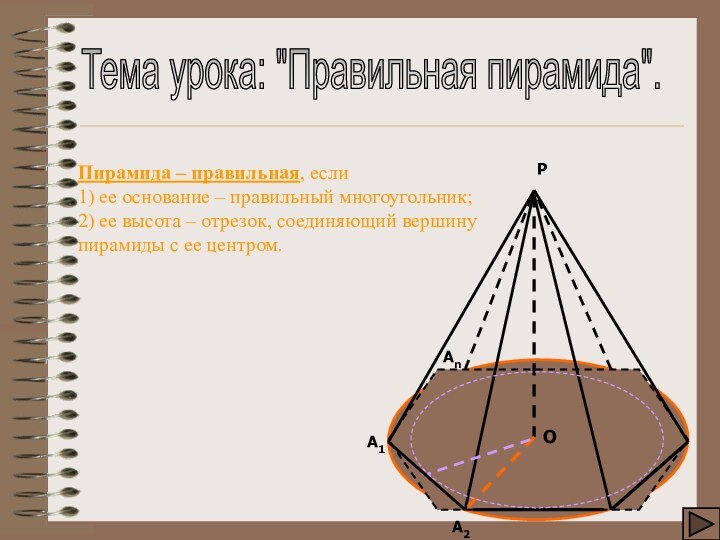
Тема урока: "Правильная пирамида".
Пирамида – правильная, если
1) ее
основание – правильный многоугольник;
2) ее высота – отрезок, соединяющий
вершину пирамиды с ее центром.
Слайд 11
В правильной пирамиде:
Боковые ребра образуют равные
углы с плоскостью основания
Боковые ребра образуют равные углы с
высотойБоковые грани образуют равные углы с основанием
Высота пирамиды образует равные углы с высотами боковых граней
Апофемы равны
Слайд 12
Апофема.
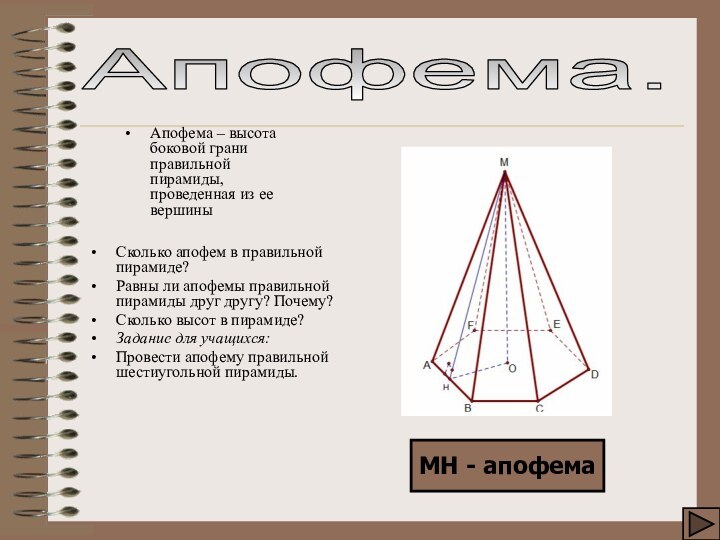
МН - апофема
Апофема – высота боковой грани правильной
пирамиды, проведенная из ее вершины
Сколько апофем в правильной
пирамиде? Равны ли апофемы правильной пирамиды друг другу? Почему?
Сколько высот в пирамиде?
Задание для учащихся:
Провести апофему правильной шестиугольной пирамиды.
Слайд 13
В правильной четырехугольной пирамиде построить:
а)
угол между боковым ребром и плоскостью основания;
б) линейный угол
двугранного угла при основании;в) линейный угол двугранного угла между боковыми гранями.
Задача.
Слайд 14
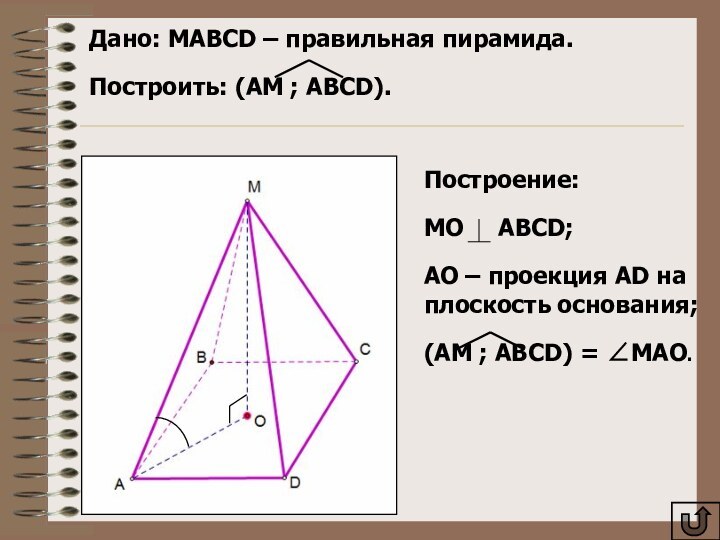
Дано: MAВCD – правильная пирамида.
Построить: (AM ;
ABCD).
Построение:
МО ABCD;
AO – проекция AD на
плоскость основания;(AM ; ABCD) = МAO.
Слайд 15
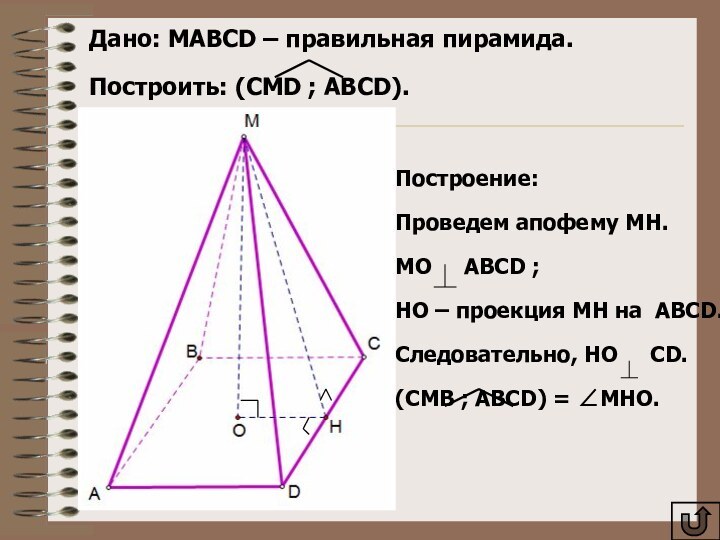
Дано: MAВCD – правильная пирамида.
Построить: (CMD ;
ABCD).
Построение:
Проведем апофему МН.
МO AВСD ;
НО –
проекция МН на ABCD.Следовательно, НО CD.
(СMВ ; ABCD) = МНО.
Слайд 16
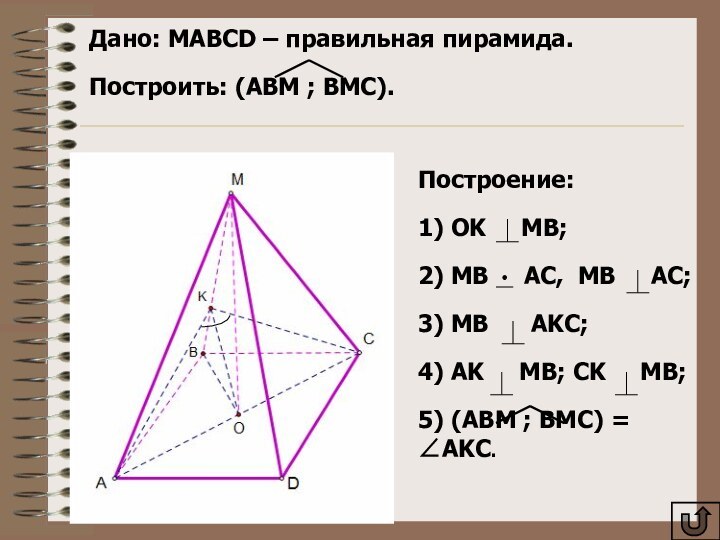
Дано: MAВCD – правильная пирамида.
Построить: (AВM ;
BМC).
Построение:
1) OK MB;
2) MB
AC, MB AC;3) MB AKC;
4) AK MB; CK MB;
5) (ABM ; BMC) = AKC.
Слайд 18
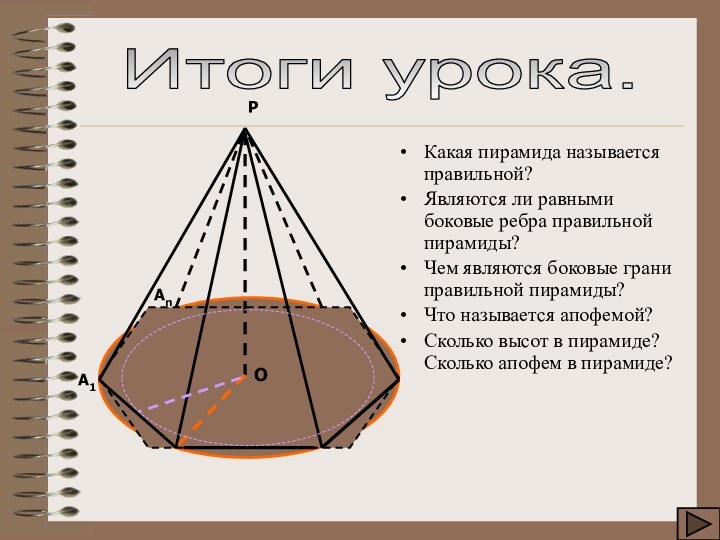
Итоги урока.
Какая пирамида называется правильной?
Являются ли равными
боковые ребра правильной пирамиды?
Чем являются боковые грани правильной пирамиды?
Что
называется апофемой?Сколько высот в пирамиде? Сколько апофем в пирамиде?