Презентация на тему Правильная пирамида

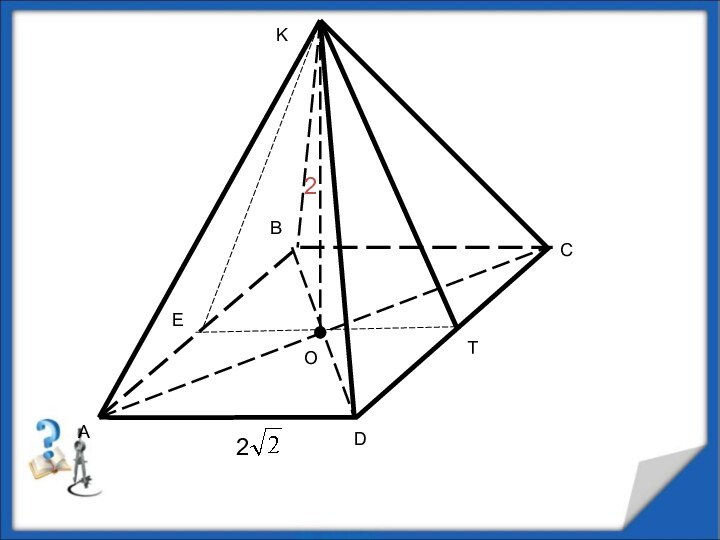
2 и длина высоты 2.

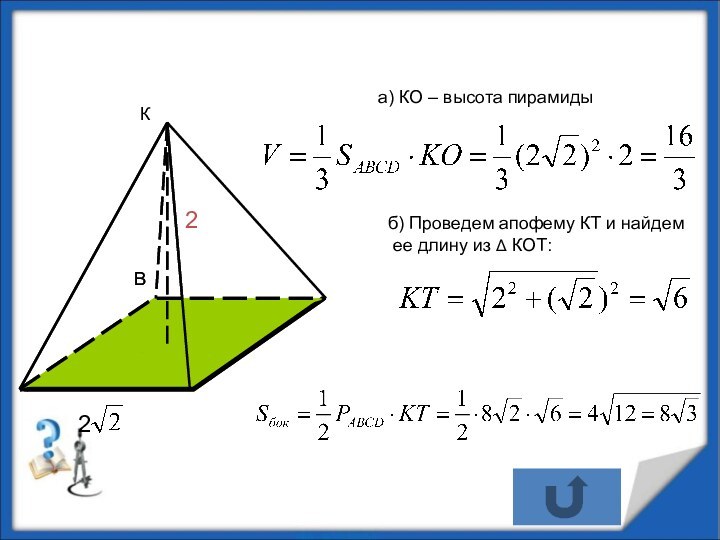
Найдите:
а) объем пирамиды;
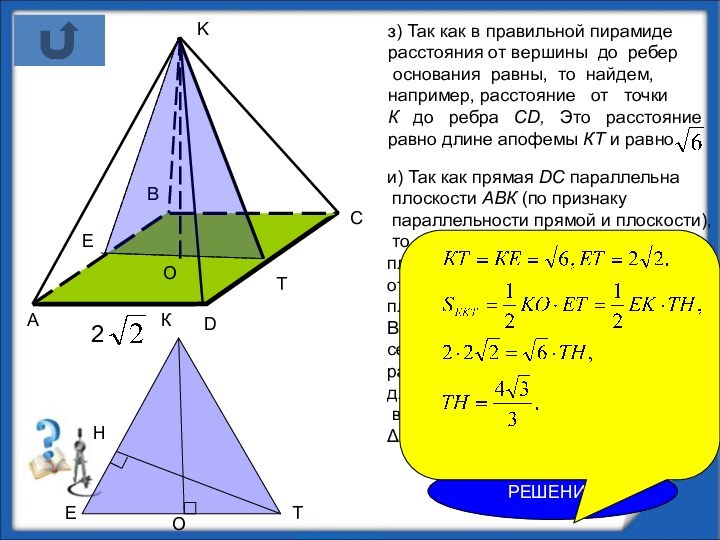
б) площадь боковой по­верхности;
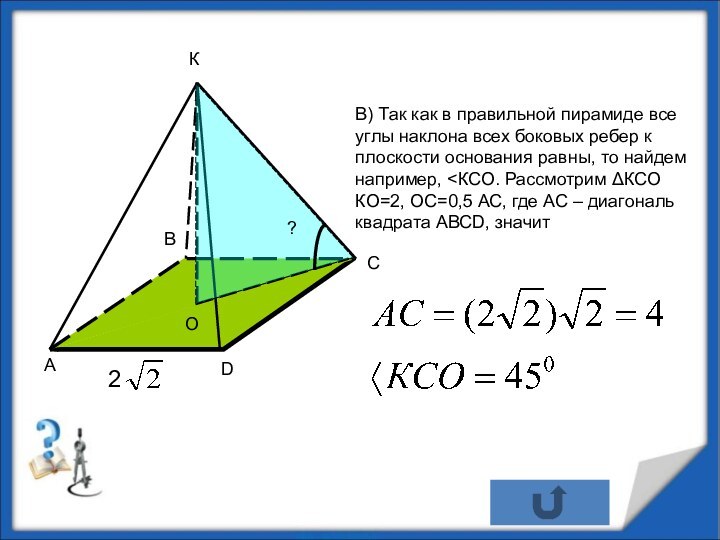
в) угол наклона бокового ребра к плоскости основания;
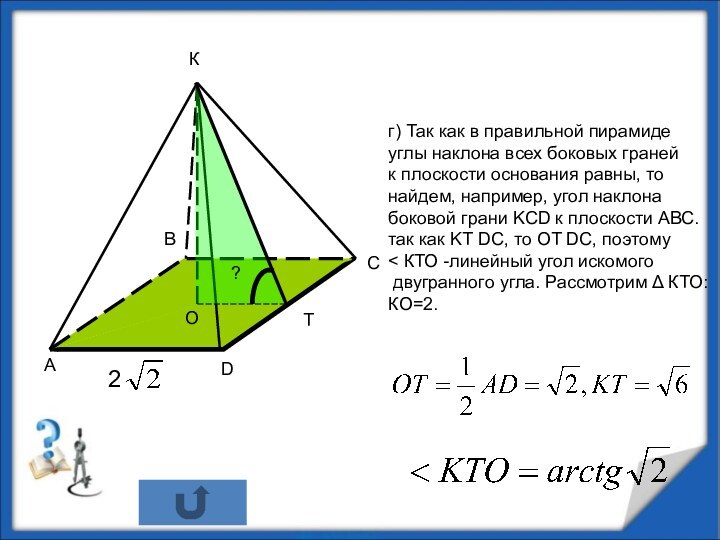
г) угол наклона боковой грани к плоскости основания;
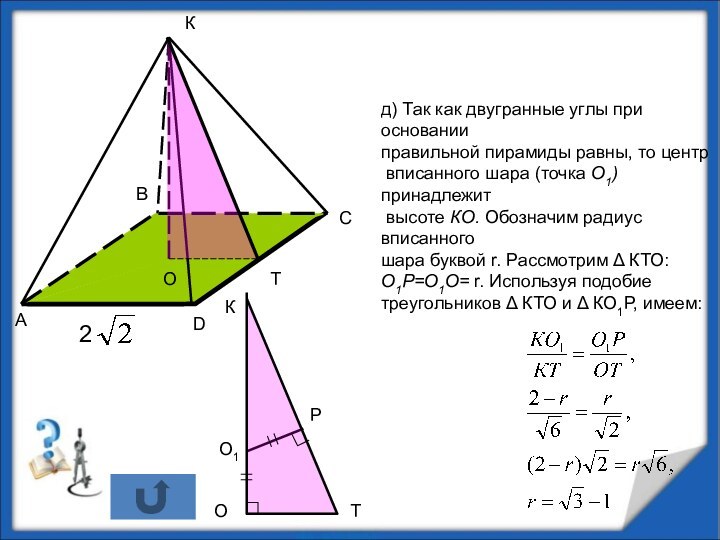
д) радиус вписанного шара;
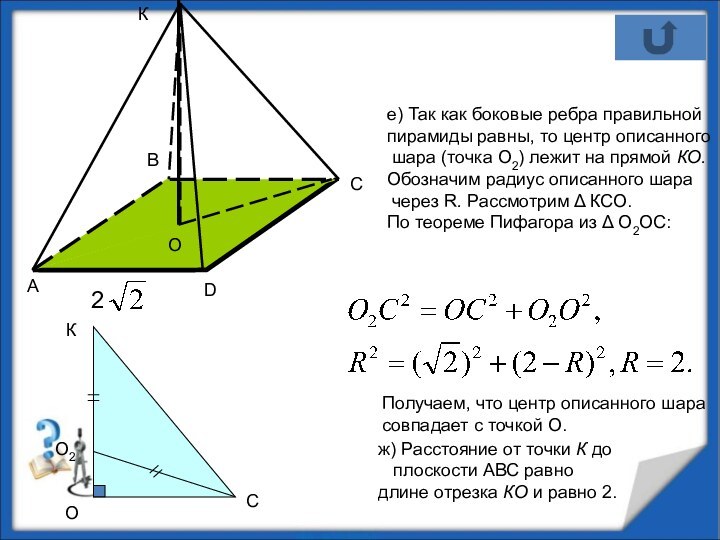
е) радиус описанного шара;
ж) расстояние от вершины пирамиды до плоскости основания;

и) расстояние от ребра основания до противоположной грани;
к)

расстояние между боковым ребром и скрещивающейся с ним диагональю ос­нования;
л) объем вписанного конуса;
м) площадь боковой поверхности описанного конуса.

Выход

и найдем
ее длину из Δ КОТ:
В

всех боковых ребер к
плоскости основания равны, то найдем

например, <КСО. Рассмотрим ΔКСО
КО=2, ОС=0,5 АС, где АС – диагональ
квадрата АВСD, значит

К

О

?

боковых граней
к плоскости основания равны, то
найдем, например, угол

наклона
боковой грани KCD к плоскости АВС.
так как KT DC, то OT DC, поэтому
< КТО -линейный угол искомого
двугранного угла. Рассмотрим Δ КТО:
КО=2.

Т

К

О

?

пирамиды равны, то центр
вписанного шара (точка О1) принадлежит

высоте КО. Обозначим радиус вписанного
шара буквой r. Рассмотрим Δ КТО:
О1Р=О1О= r. Используя подобие треугольников Δ КТО и Δ КО1Р, имеем:

К

Т

О

то центр описанного
шара (точка О2) лежит на прямой

КО.
Обозначим радиус описанного шара
через R. Рассмотрим Δ КСО.
По теореме Пифагора из Δ О2ОС:

Получаем, что центр описанного шара
совпадает с точкой О.

К

О

О2

О

К

С

ж) Расстояние от точки К до
плоскости АВС равно длине отрезка КО и равно 2.

вершины до ребер
основания равны, то найдем,
например,

расстояние от точки
К до ребра СD, Это расстояние равно длине апофемы КТ и равно

K

O

T

и) Так как прямая DС параллельна
плоскости АВК (по признаку
параллельности прямой и плоскости),
то расстояние от прямой DС до
плоскости АВК равно расстоянию
от любой точки прямой DС до этой
плоскости. Рассмотрим на прямой
ВС точку Т. И из Δ ЕКТ (точка Е —
середина АВ) найдем искомое
расстояние. Это расстояние равно
длине высоты ТН. Найдем длину ТН,
выразив двумя способами площадь
Δ ЕКТ.

Е

РЕШЕНИЕ

ВD.Проведем высоту OF в Δ КСО и докажем ,

что
OF- общий перпендикуляр к прямым КС и ВD.

1) OF┴ КС по построению
2) Так как ВD ┴(КСО) (По признаку
перпендикулярности прямой и
Плоскости), а OF (КСО), то ВD┴OF
3)Найдем длину OF, используя
площадь Δ КСО

О

F

перпендикуляр прямых KC
и BD. Найдем длину вектора SN
2)Так

как SD коллинеарен BD, то
существует такое число х, что

Найдем координаты векторов:

Векторно-координатный метод

z

x

y

K

O

S

N

радиус основания конуса
равен радиусу окружности, вписанной в
квадрат

АВСD, поэтому

м) Образующая описанного конуса равна
боковому ребру пирамиды, а радиус
основания конуса равен радиусу
окружности, описанной около квадрата
АВСD, поэтому

K

O