Презентация на тему Правильные многогранники

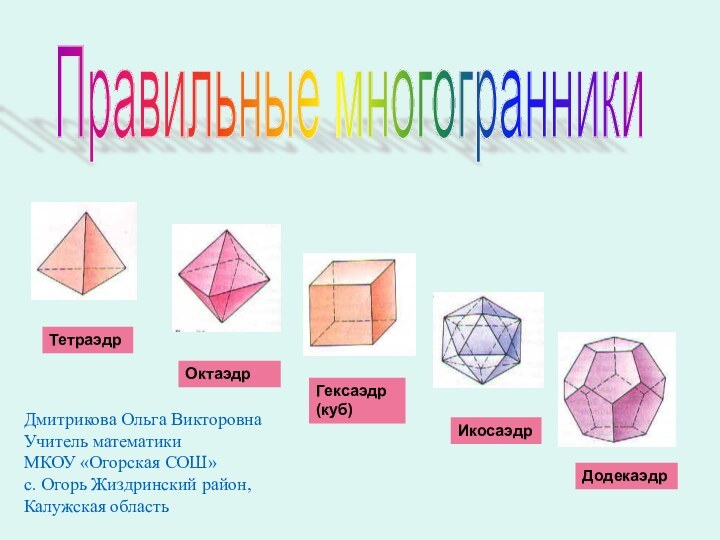
вершина устремлена вверх;
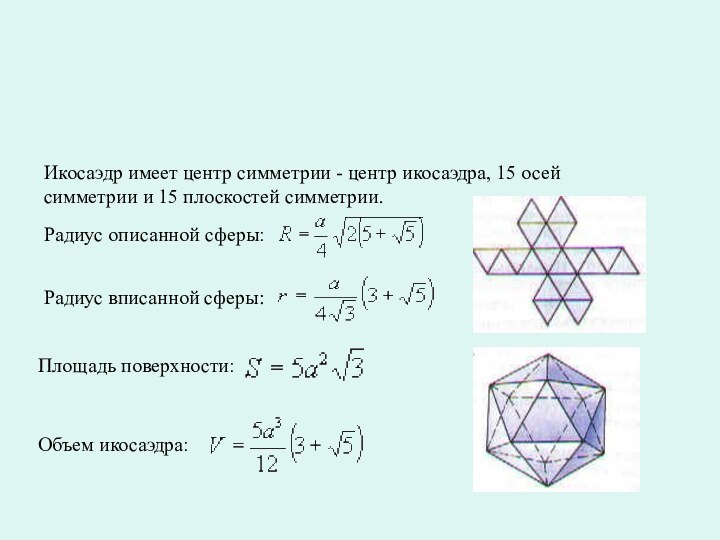
Икосаэдр — Воду, так как он

самый «обтекаемый» многогранник;
Куб — Землю, как самый «устойчивый» многогранник;
Октаэдр — Воздух, как самый «воздушный» многогранник.
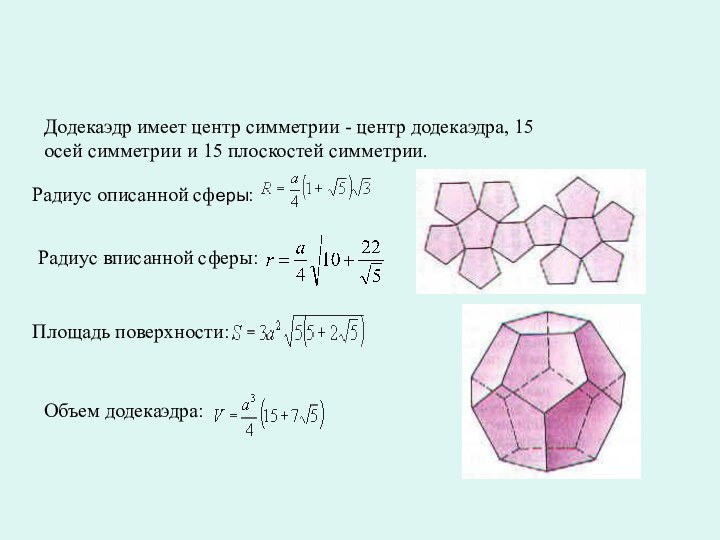
Додекаэдр- воплощал в себе «все сущее», «Вселенский разум», символизировал все мироздание и считался главной геометрической фигурой мироздания.

его вершина является вершиной трех треугольников. Сумма плоских углов

при каждой вершине равна 180 градусов. Таким образом, тетраэдр имеет 4 грани, 4 вершины и 6 ребер.

3 оси симметрии и 6 плоскостей симметрии.

Радиус вписанной сферы:
Радиус

описанной сферы:

Площадь поверхности:

Объем тетраэдра:

Каждая его вершина является вершиной четырех треугольников. Сумма плоских

углов при каждой вершине равна 240 градусов. Таким образом, октаэдр имеет 8 граней, 6 вершин и 12 ребер.

9 осей симметрии и 9 плоскостей симметрии.
Радиус описанной сферы:
Радиус

вписанной сферы:

Площадь поверхности

Объем октаэдра:

Каждая его вершина является вершиной трех квадратов. Сумма плоских

углов при каждой вершине равна 270 градусов. Таким образом, куб имеет 6 граней, 8 вершин и 12 ребер.

куба, 9 осей симметрии
и 9 плоскостей симметрии.
Радиус описанной

сферы:

Радиус вписанной сферы:

Площадь поверхности куба:

Объем куба:

его вершина является вершиной пяти треугольников. Сумма плоских углов

при каждой вершине равна 300 градусов. Таким образом икосаэдр имеет 20 граней, 12 вершин и 30 ребер.

15 осей симметрии и 15 плоскостей симметрии.
Радиус описанной сферы:
Радиус

вписанной сферы:

Площадь поверхности:

Объем икосаэдра:

пятиугольников. Каждая его вершина является вершиной трех пятиугольников. Сумма

плоских углов при каждой вершине равна 324 градусов. Таким образом, додекаэдр имеет 12 граней, 20 вершин и 30 ребер.

додекаэдра, 15 осей симметрии и 15 плоскостей симметрии.
Радиус описанной

сферы:

Радиус вписанной сферы:

Площадь поверхности:

Объем додекаэдра: