- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Правильные многоугольники
Содержание
- 2. Выпуклый многоугольник называется правильным, если у него все углы равны и все стороны равны
- 3. Известно, что сумма всех внутренних углов выпуклого n-угольника равна (n-2)·180ºα=60ºα=90ºα=n - 2 n·180ºα=108ºα=120º180º360º540º720º
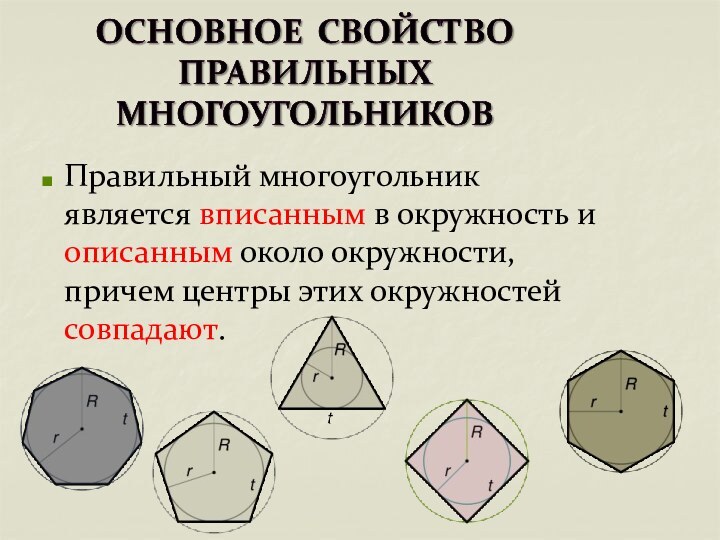
- 4. Правильный многоугольник является вписанным в окружность и описанным около окружности, причем центры этих окружностей совпадают.
- 5. 1. вычислить периметр и площадь правильного треугольника
- 6. Задача 1. Радиус окружности, вписанной в квадрат,
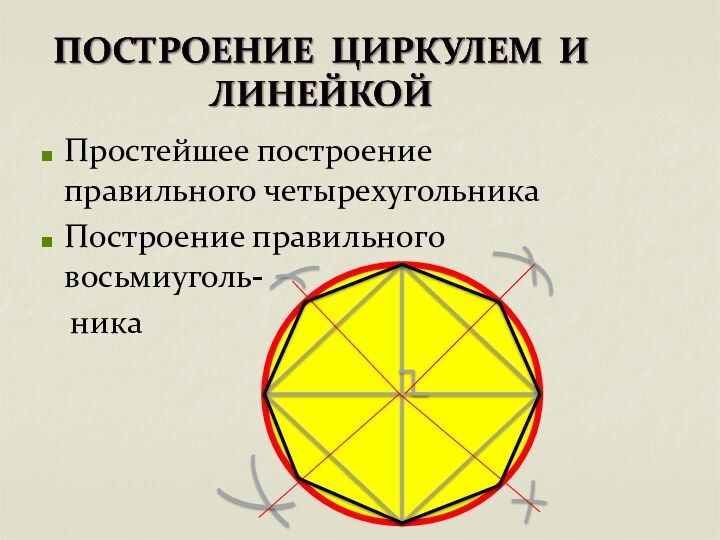
- 7. Простейшее построение правильного четырехугольникаПостроение правильного восьмиуголь- ника
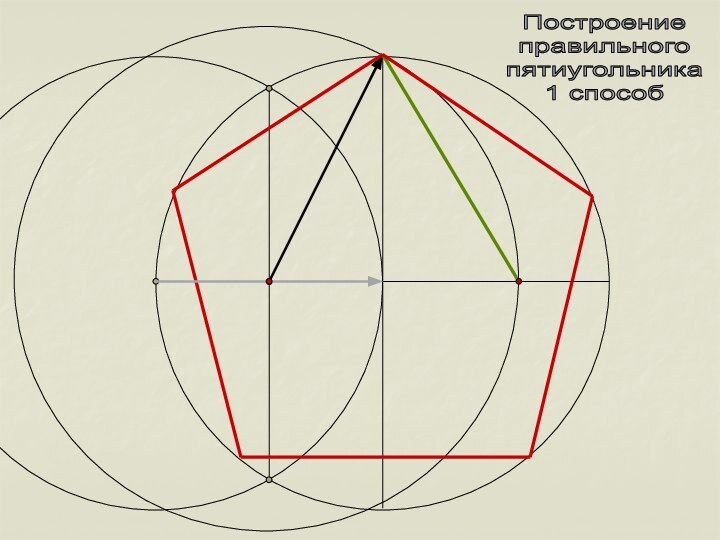
- 8. Построениеправильногопятиугольника1 способ
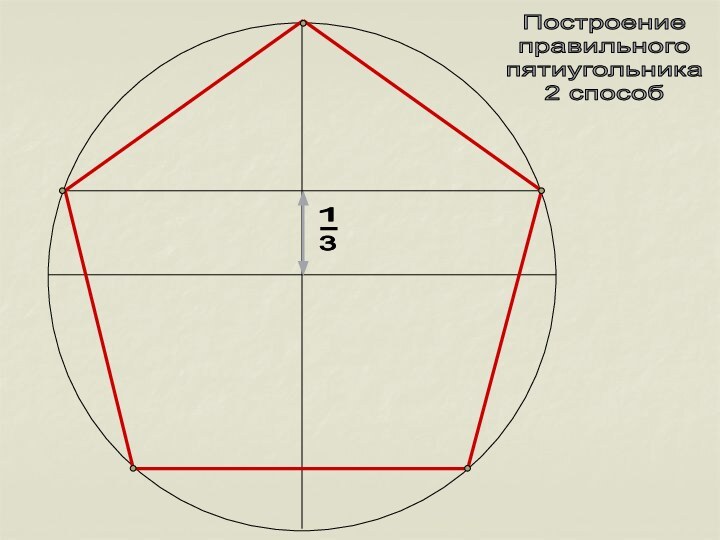
- 9. Построениеправильногопятиугольника2 способ
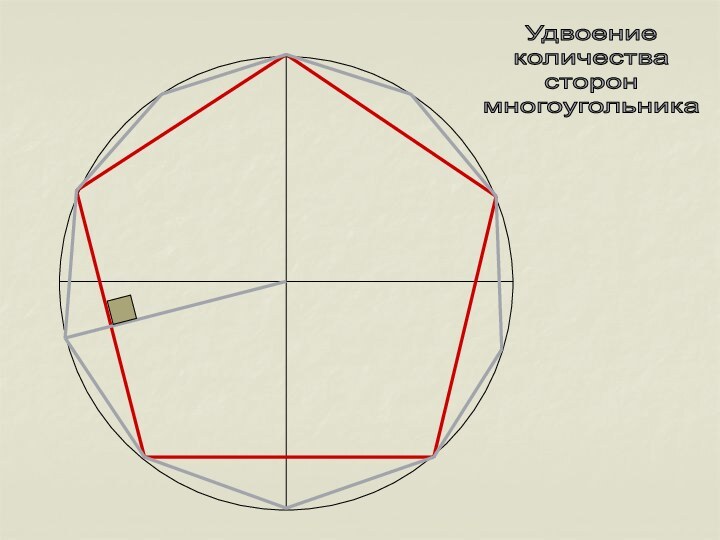
- 10. Удвоение количества сторонмногоугольника
- 11. Паркетыиз правильныхмногоугольников
- 12. Построение правильных многоугольников, то есть деление окружности
- 13. Именно в школе ПИФАГОРА зародилось учение о
- 14. По некоторым источникам, он являлся автором сочинения
- 15. Описал построение правильных 3 , 4 , 5 , 6- угольников, построил правильный 15-угольник
- 16. Развитие готического стиля и широкое применение витражей
- 17. Именно Альбрехт Дюрер осуществил новое построение
- 18. Дюрер занимался фортификацией, разрабатывая системы оборонительных сооружений;Решил задачу построения правильного восьмиугольника;Разработал принципы черчения художественно исполненных букв.
- 19. Для своего друга Луки Пачоли Леонардо, глубоко
- 20. математик Иоганн Кеплер создал трактат «Новогодний подарок
- 21. Доказал возможность построения правильного 17-угольника. После этого 19-летний юноша решил заняться математикой, а не филологией.
- 22. Скачать презентацию
- 23. Похожие презентации
Выпуклый многоугольник называется правильным, если у него все углы равны и все стороны равны
Слайд 2 Выпуклый многоугольник называется правильным, если у него все
углы равны и все стороны равны
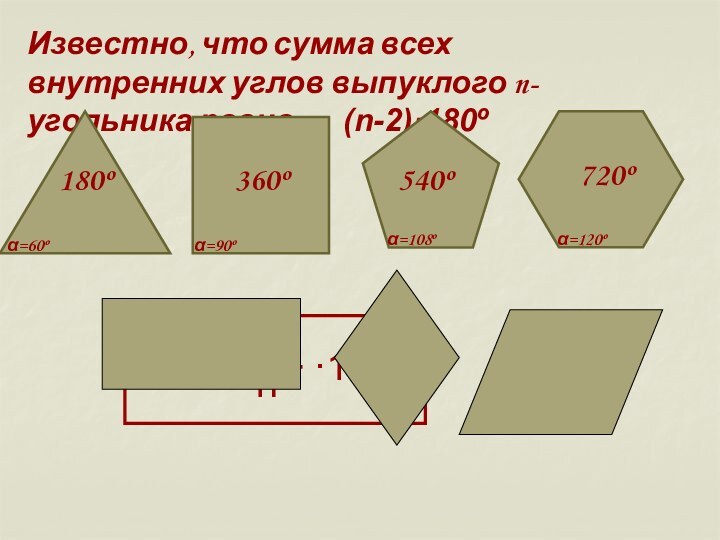
Слайд 3 Известно, что сумма всех внутренних углов выпуклого n-угольника
равна (n-2)·180º
α=60º
α=90º
α=
n - 2
n
·180º
α=108º
α=120º
180º
360º
540º
720º
Слайд 4 Правильный многоугольник является вписанным в окружность и описанным
около окружности, причем центры этих окружностей совпадают.
Слайд 5 1. вычислить периметр и площадь правильного треугольника со
стороной 4 см.
2. вычислить периметр и площадь
правильного четырехугольника со стороной 3 см.
3. вычислить периметр и площадь правильного четырехугольника со стороной 2 см.
Слайд 6 Задача 1. Радиус окружности, вписанной в квадрат, равен
1 см. Найдите радиус R описанной окружности около этого
квадрата. (Задача 2. Периметр правильного шестиугольника, описанного около окружности, равен 6⩗3см. Чему равен радиус этой окружности?Задача 3. Периметр квадрата, вписанного в окружность, равен 4⩗2 см. Найдите радиус r вписанной окружности.
Слайд 12 Построение правильных многоугольников, то есть деление окружности на
равные части, позволяло решать практические задачи:
1)Создание колеса со спицами;
2)Деление
циферблата часов;3)Строительство античных театров;
4)Создание астрономических сооружений
Слайд 13 Именно в школе ПИФАГОРА зародилось учение о правильных
многоугольниках; кроме того, пифагорейцы рассмотрели вопрос покрытия плоскости правильными
многоугольниками.Слайд 14 По некоторым источникам, он являлся автором сочинения о
правильных многоугольниках, часто присоединяемого к "Началам" в качестве XV
книги. Исидор из Милета (532-537 гг.) - византийский архитектор и геометр, построивший вместе с Анфи - мием собор Святой Софии в Константинополе.Слайд 16 Развитие готического стиля и широкое применение витражей в
строительстве соборов также заставило вернуться к задачам построения правильных
многоугольников.Слайд 17 Именно Альбрехт Дюрер осуществил новое построение правильного
пятиугольника, передав потомкам средневековый способ построения постоянным раствором циркуля.
Слайд 18
Дюрер занимался фортификацией, разрабатывая системы оборонительных сооружений;
Решил задачу
построения правильного восьмиугольника;
Разработал принципы черчения художественно исполненных букв.
Слайд 19 Для своего друга Луки Пачоли Леонардо, глубоко интересующийся
пропорциями, создал иллюстрации многогранников, гранями которых являются правильные многоугольники.
Слайд 20 математик Иоганн Кеплер создал трактат «Новогодний подарок или
о шестиугольных снежинках», опубликованный в 1611 году. В нем
он практически привел первый пример разбиения плоскости на правильные шестиугольники.Слайд 21 Доказал возможность построения правильного 17-угольника. После этого 19-летний
