- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Преобразование плоскости
Содержание
- 2. ДВИЖЕНИЯОбразуют специальный класс преобразований,играющих особую роль в
- 3. ДВИЖЕНИЕ или ПЕРЕМЕЩЕНИЕ - это преобразование плоскости, сохраняющее расстояния
- 5. При движении репер
- 6. СВОЙСТВА ДВИЖЕНИЯ 1.
- 7. СВОЙСТВА ДВИЖЕНИЯ2. Движение переводит полуплоскость с
- 8. СВОЙСТВА ДВИЖЕНИЯ3. Движение сохраняет простое отношение трех точек прямой.АВСλ =AC : CBA1B1C1λ1=A1C1 : C1B1λ =λ 1
- 9. СВОЙСТВА ДВИЖЕНИЯ4. Движение сохраняет отношение «лежать между».5.
- 10. СВОЙСТВА ДВИЖЕНИЯ6. Движение переводит угол в равный ему угол, луч в лучAA1A=A1АМА 'М 'АМА'М'
- 11. СВОЙСТВА ДВИЖЕНИЯ7. Движение переводит взаимно перпендикулярные прямые во взаимно перпендикулярные прямыеаba'b'движение
- 12. СВОЙСТВА ДВИЖЕНИЯ8. При движении флаг переводится во
- 14. Преобразование точек плоскости сохраняет ориентацию плоскости или
- 15. ВИДЫ ДВИЖЕНИЙДвижение, не меняющее ориентацию, называетсяДВИЖЕНИЕМ I РОДАДвижение, меняющее ориентацию, называетсяДВИЖЕНИЕМ II РОДА
- 16. АНАЛИТИЧЕСКИЕ ВЫРАЖЕНИЯ ДВИЖЕНИЙx` = x∙cosα – ε∙y∙sinα
- 17. ДВИЖЕНИЕ I РОДА1. Поворот на угол АММ1Аналитические
- 18. ДВИЖЕНИЕ I РОДА2. а)Параллельный перенос наАналитические выражения:x` = x+х0y` =yб) Параллельный перенос на - тождественное преобразованиеxy
- 19. ДВИЖЕНИЕ II РОДА1.Осевая симметрияАВСаС1А1В1Аналитические выражения:x` = xy` =-yесли прямая а совпадает с осью ОХ
- 20. ДВИЖЕНИЕ II РОДА2.Скользящая симметрия (g)АВСаС1А1В1g=s*fОсевая симметрияПараллельный переносМ1М2Аналитические
- 21. ПРЕОБРАЗОВАНИЕ ПОДОБИЯ Преобразование плоскости называется преобразованием
- 22. Рассмотрим на плоскости три точки М, М0,
- 23. ПРЕОБРАЗОВАНИЕ ПОДОБИЯ (f)f = g ∙ hдвижение
- 24. ПОДОБИЕ I РОДА Аналитические выражения: x` =
- 25. 2. Параллельный перенос наОО1Аналитические выражения: x` = k∙x+ x0, y` = k∙y+ y0
- 26. ПОДОБИЕ II РОДА1. Осевая симметриямаМ1Аналитические выражения:
- 27. ПОДОБИЕ II РОДА2. Скользящая симметрияxyММ1М’Аналитические выражения: x` = k∙x+x0, y` = -k∙y
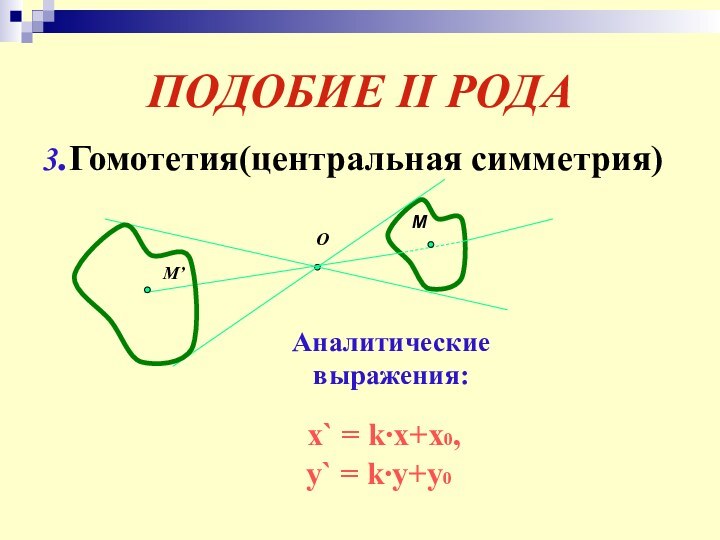
- 28. ПОДОБИЕ II РОДА3.Гомотетия(центральная симметрия)ОММ’Аналитические выражения: x` = k∙x+x0, y` = k∙y+y0
- 29. Скачать презентацию
- 30. Похожие презентации





















Слайд 2
ДВИЖЕНИЯ
Образуют специальный класс преобразований,
играющих особую роль в различных
науках и их приложениях
и технических явленийСлайд 5 При движении репер R,
образованный точками A, В, С, переходит в репер R',
образованный точками A', B', C', причем это движение единственно.А
В
С
R:
A'
B'
C'
R' :
Слайд 6
СВОЙСТВА ДВИЖЕНИЯ
1. Движение
переводит прямую в прямую, параллельную прямую в параллельную ей
прямую.а
движение
а '
а || а '
Слайд 7
СВОЙСТВА ДВИЖЕНИЯ
2. Движение переводит полуплоскость с границей
A в полуплоскость c границей А', где А' –
образ прямой a.а
a’
Образ прямой а
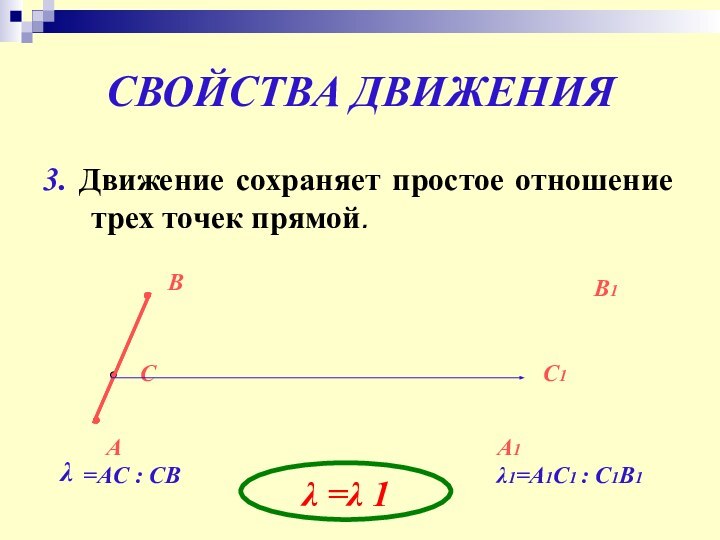
Слайд 8
СВОЙСТВА ДВИЖЕНИЯ
3. Движение сохраняет простое отношение трех точек
прямой.
А
В
С
λ
=AC : CB
A1
B1
C1
λ1=A1C1 : C1B1
λ =λ 1
Слайд 9
СВОЙСТВА ДВИЖЕНИЯ
4. Движение сохраняет отношение «лежать между».
5. Движение
переводит отрезок AB в отрезок A'B'. При этом середина
отрезка AB переходит в середину отрезка A'B'.
Слайд 10
СВОЙСТВА ДВИЖЕНИЯ
6. Движение переводит угол в равный ему
угол,
луч в луч
A
A1
A=
A1
А
М
А '
М '
АМ
А'М'
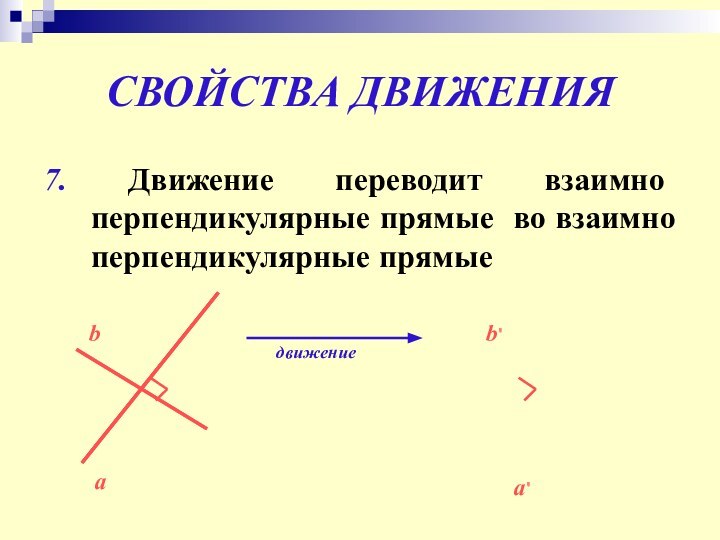
Слайд 11
СВОЙСТВА ДВИЖЕНИЯ
7. Движение переводит взаимно перпендикулярные прямые во
взаимно перпендикулярные прямые
а
b
a'
b'
движение
Слайд 12
СВОЙСТВА ДВИЖЕНИЯ
8. При движении флаг переводится во флаг,
где флаг - это тройка, состоящая из точки, луча
и полуплоскостиСлайд 14 Преобразование точек плоскости сохраняет ориентацию плоскости или меняет
ориентацию плоскости,
если любой репер и его образ
сохраняют или
меняют ориентацию
Слайд 15
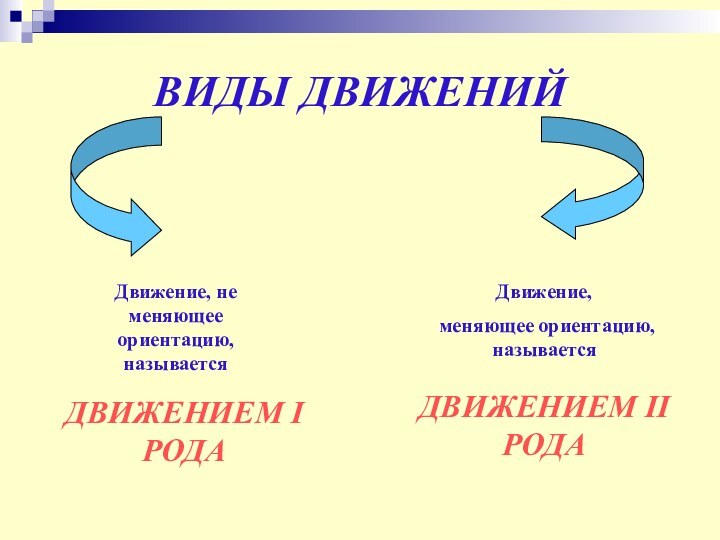
ВИДЫ ДВИЖЕНИЙ
Движение, не меняющее ориентацию, называется
ДВИЖЕНИЕМ I РОДА
Движение,
меняющее ориентацию, называется
ДВИЖЕНИЕМ II РОДА
Слайд 16
АНАЛИТИЧЕСКИЕ ВЫРАЖЕНИЯ ДВИЖЕНИЙ
x` = x∙cosα – ε∙y∙sinα +
x0,
y` = x∙sinα + ε∙y∙cosα + y0
при ε =
1 ДВИЖЕНИЕ
I РОДА
при ε = -1
ДВИЖЕНИЕ
II РОДА
Слайд 17
ДВИЖЕНИЕ I РОДА
1. Поворот на угол
А
М
М1
Аналитические выражения:
x`
= x∙cosα – y∙sinα ,
y` = x∙sinα + y∙cosα
а) тождественное преобразование,
б) центральная симметрия,
x` = x
y` = y
x` =- x+х0
y` =- y+y0
Слайд 18
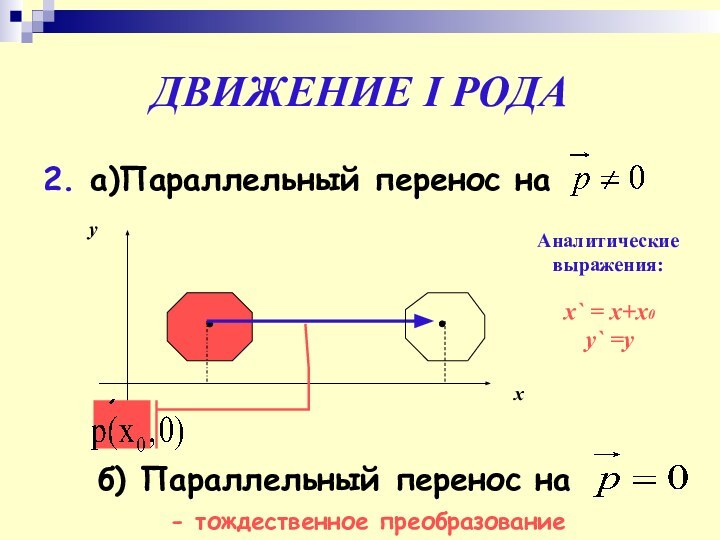
ДВИЖЕНИЕ I РОДА
2. а)Параллельный перенос на
Аналитические выражения:
x` =
x+х0
y` =y
б) Параллельный перенос на
- тождественное преобразование
x
y
Слайд 19
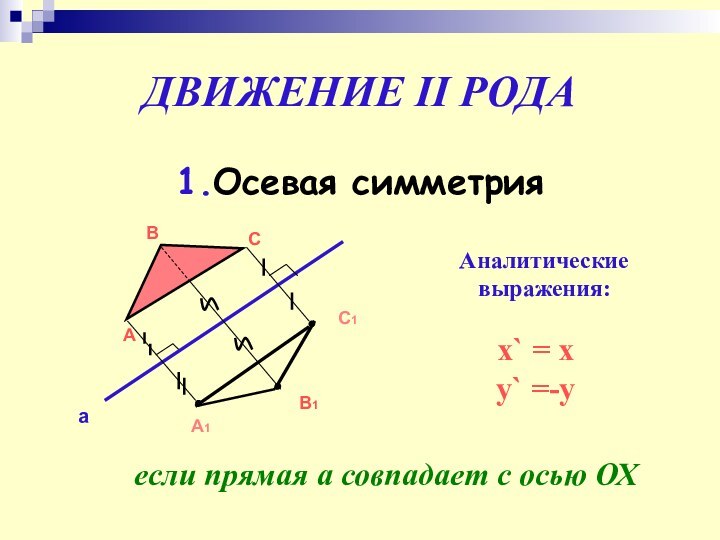
ДВИЖЕНИЕ II РОДА
1.Осевая симметрия
А
В
С
а
С1
А1
В1
Аналитические выражения:
x` = x
y` =-y
если
прямая а совпадает с осью ОХ
Слайд 20
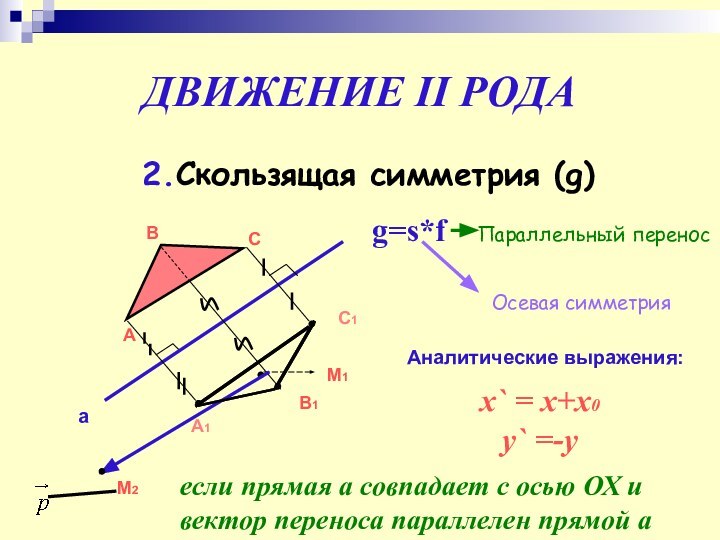
ДВИЖЕНИЕ II РОДА
2.Скользящая симметрия (g)
А
В
С
а
С1
А1
В1
g=s*f
Осевая симметрия
Параллельный перенос
М1
М2
Аналитические выражения:
x`
= x+x0
y` =-y
если прямая а совпадает с осью ОХ
и вектор переноса параллелен прямой а
Слайд 21
ПРЕОБРАЗОВАНИЕ
ПОДОБИЯ
Преобразование плоскости называется преобразованием подобия, если
существует k > 0, такое что для любых точек
A, B, A`, B` выполняется равенство:A`B` = kAB
При k =1 преобразование подобия является движением
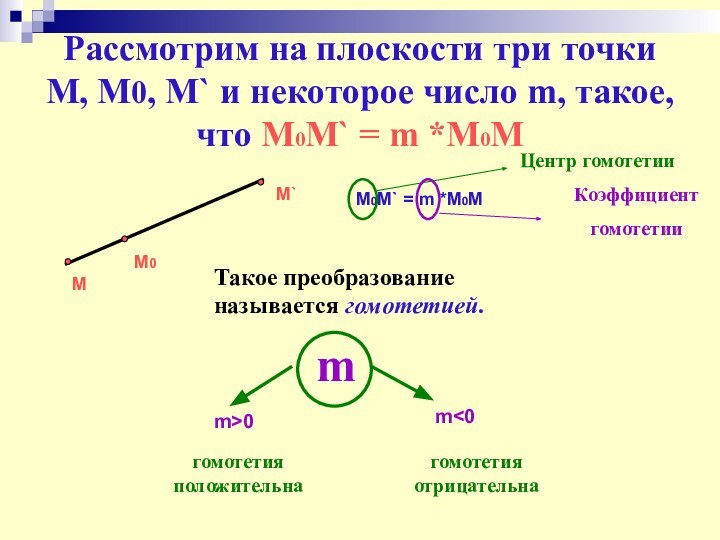
Слайд 22 Рассмотрим на плоскости три точки М, М0, M`
и некоторое число m, такое, что М0M` = m
*М0MМ0
М
M`
М0M` = m *М0M
Такое преобразование называется гомотетией.
Центр гомотетии
Коэффициент
гомотетии
m
m>0
гомотетия положительна
m<0
гомотетия отрицательна
Слайд 23
ПРЕОБРАЗОВАНИЕ
ПОДОБИЯ (f)
f = g ∙ h
движение
гомотетия с
коэффициентом k и центром в точке М0
h:
x` = k∙xy` = k∙y
g: x`` = k∙x`∙cosα – k∙ε∙y`∙sinα + x0,
y`` = k∙x`∙sinα + k∙ε∙y`∙cosα + y0
АНАЛИТИЧЕСКИЕ ВЫРАЖЕНИЯ ПОДОБИЯ
ε = 1
подобие 1-го рода
ε = -1
подобие 2-го рода
Слайд 24
ПОДОБИЕ I РОДА
Аналитические выражения:
x` = k∙x∙cosα
– k∙y∙sinα + x,
y` = k∙y∙sinα + k∙y∙cosα
+ y1. Поворот на угол
а) тождественное преобразование, если
б) центрально-подобное вращение, если
в) центрально-подобная симметрия