Презентация на тему Преобразования графиков функций

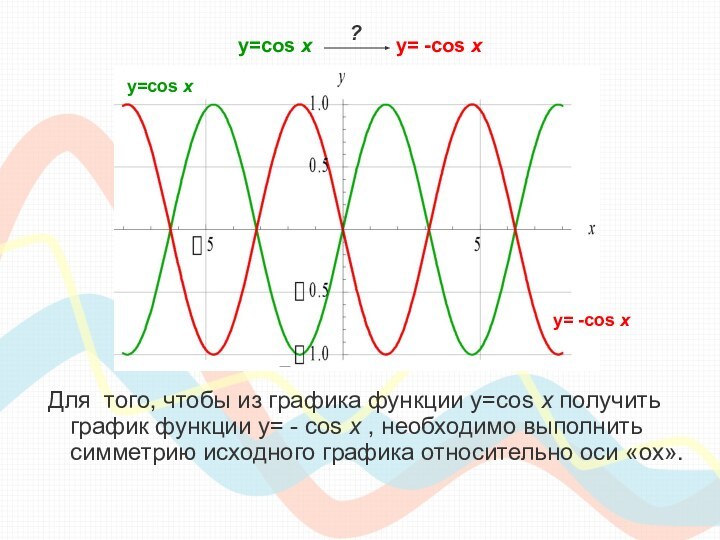
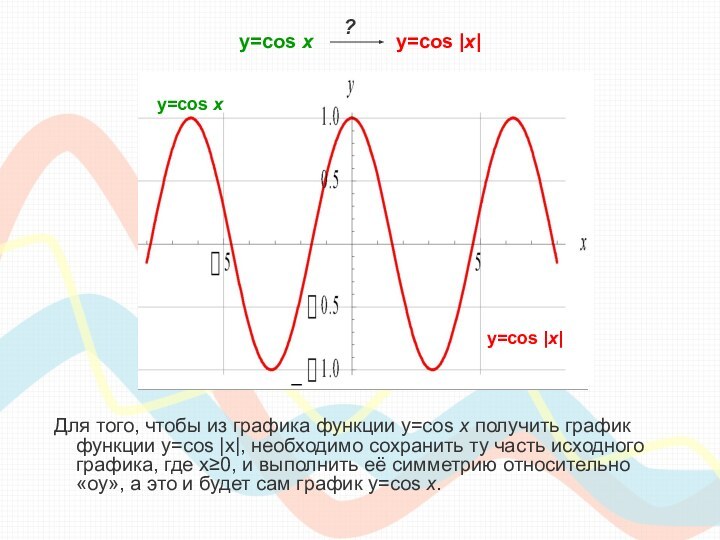
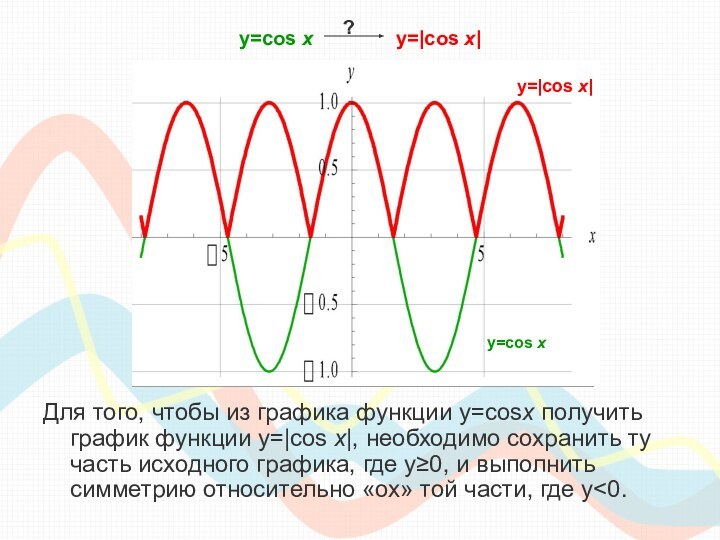
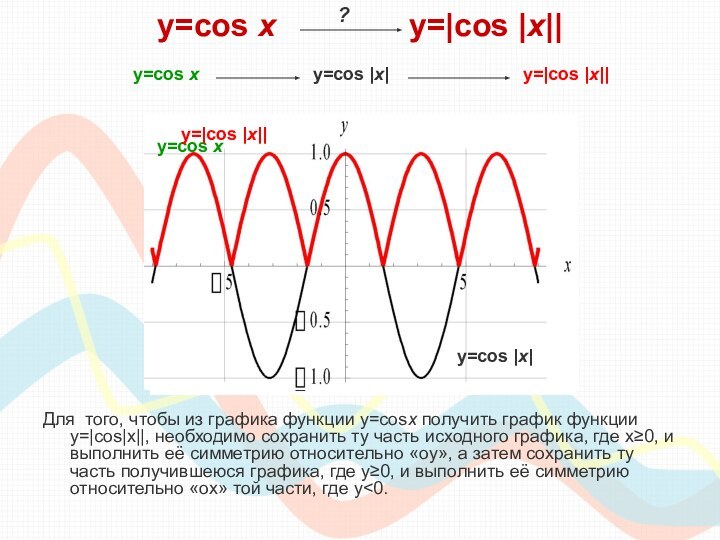
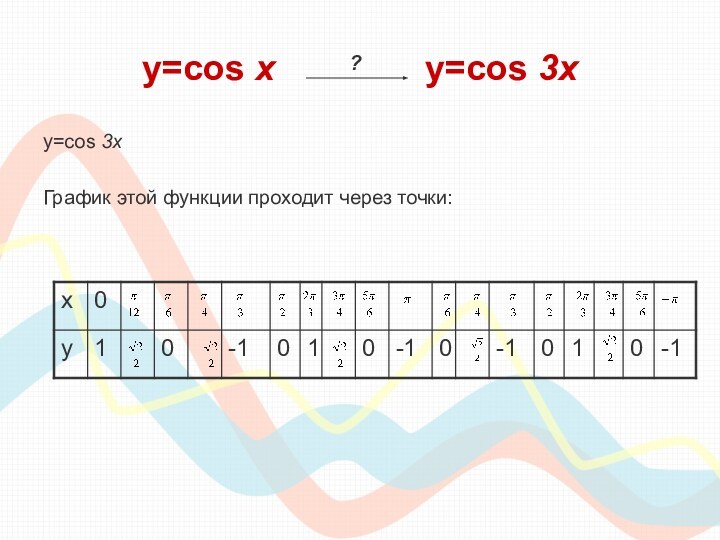
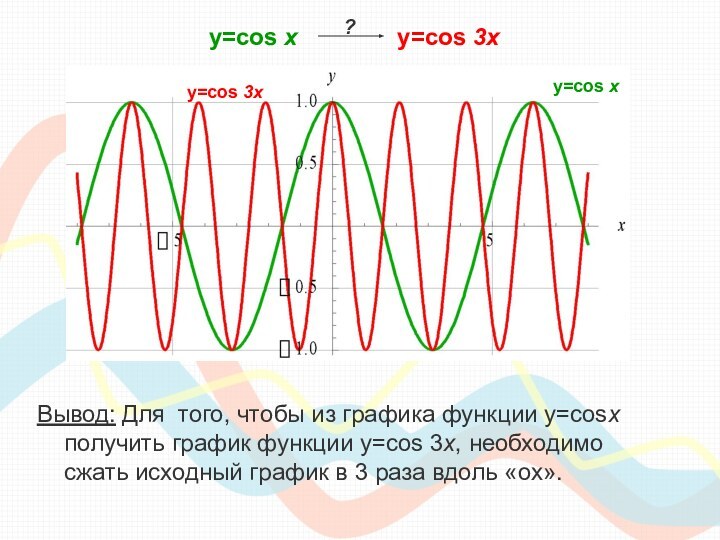
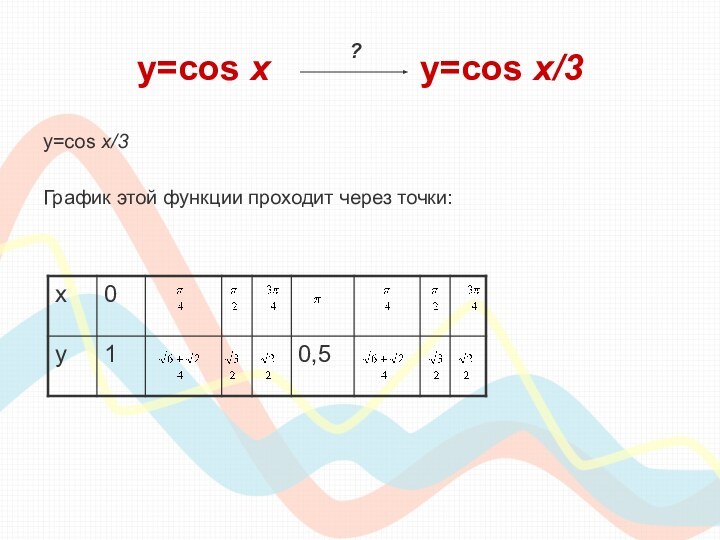
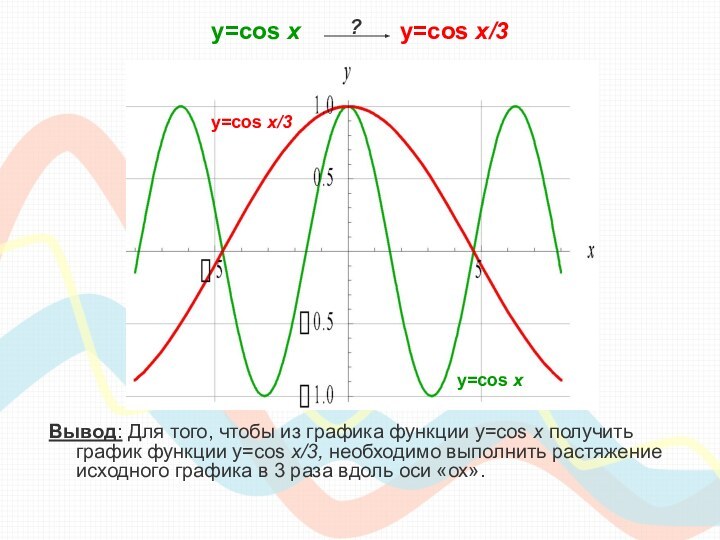
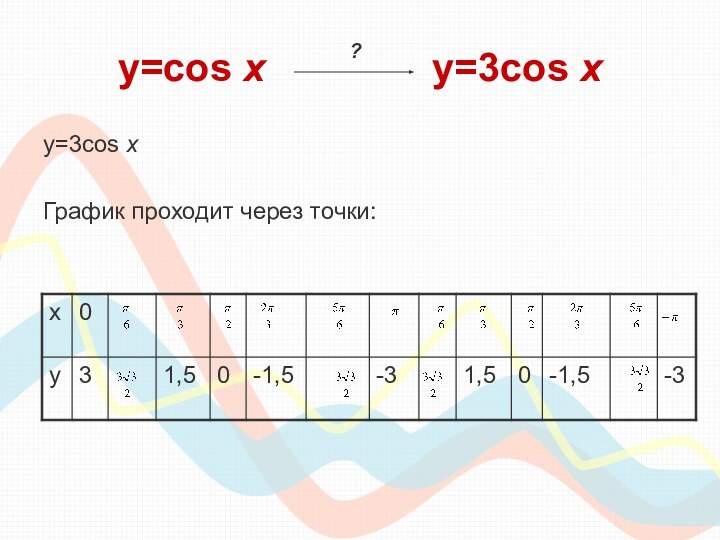
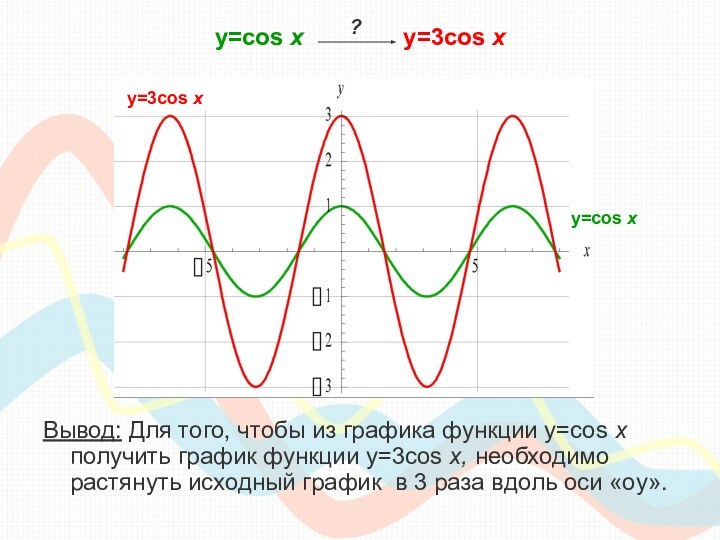
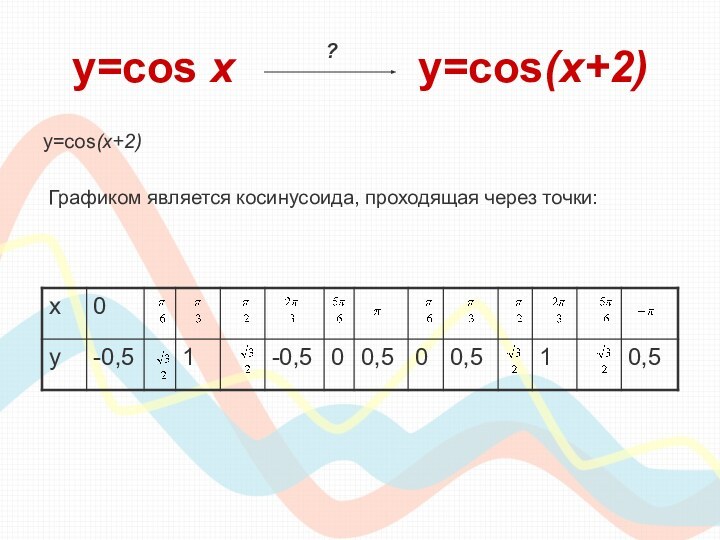
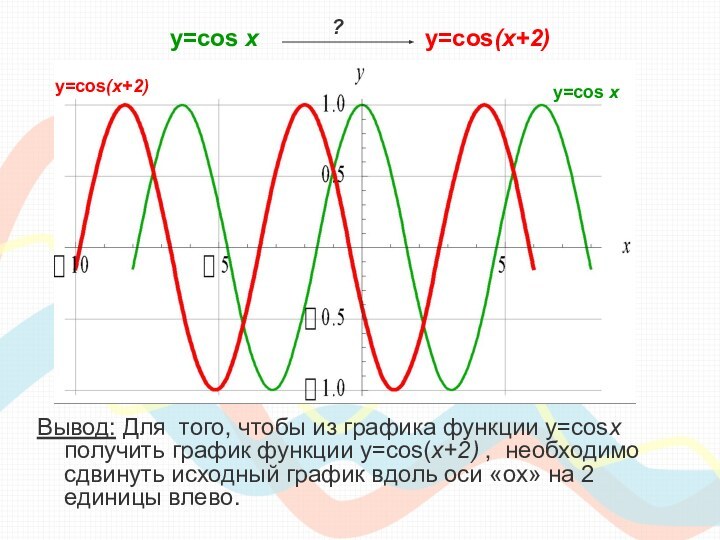
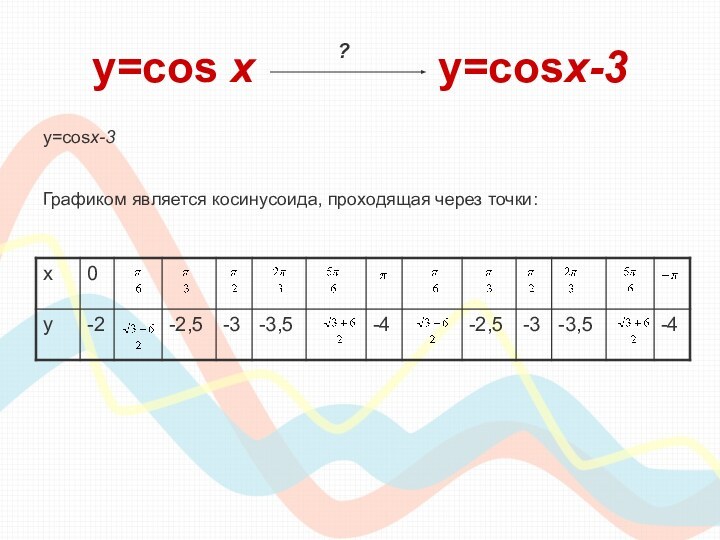
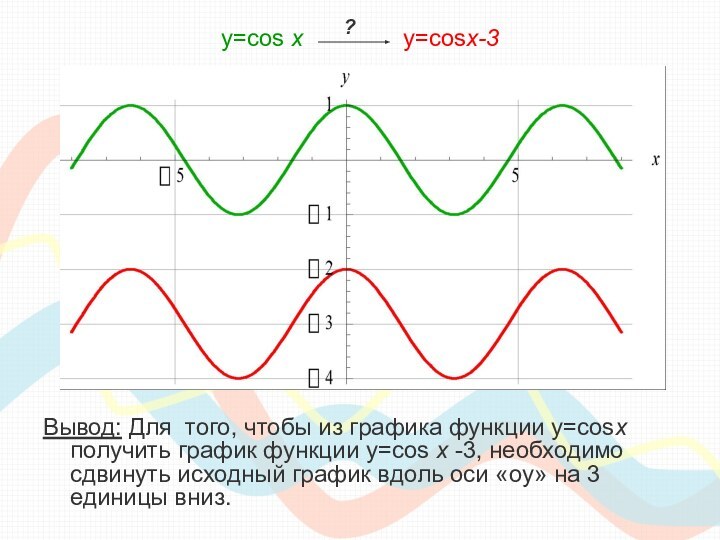
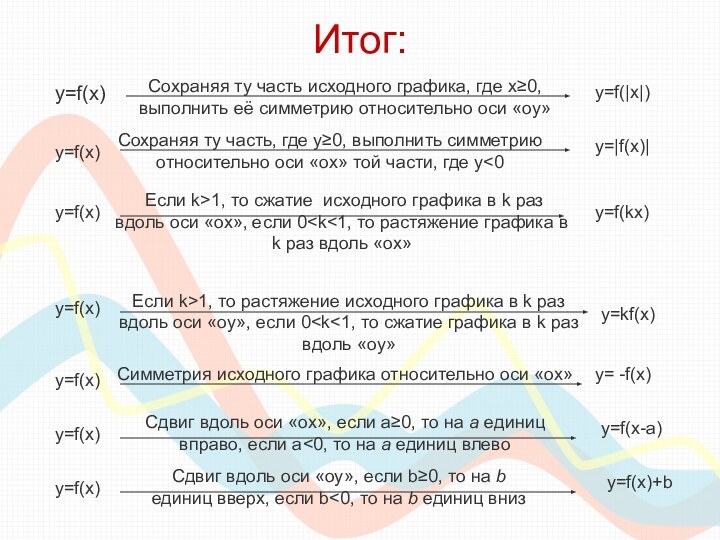
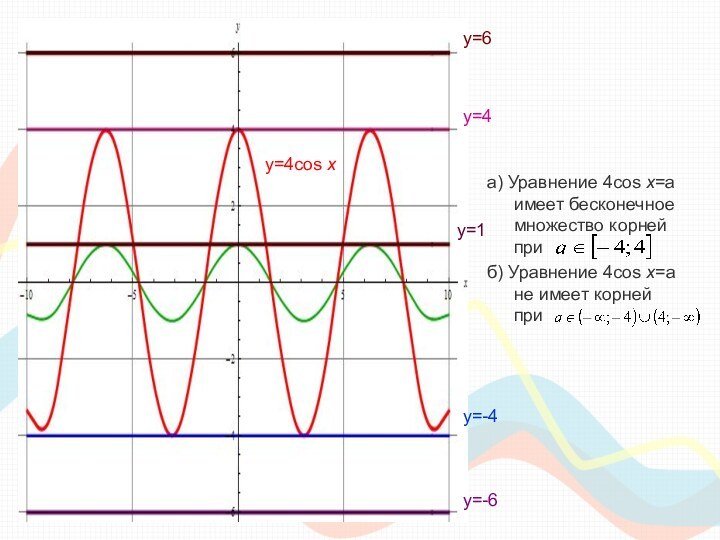
класса необходимо сдавать единый государственный экзамен по математике, куда

будут включены задания, связанные с преобразованием графиков функций.

Нами были проанализированы различные собрания с экзаменационными заданиями.

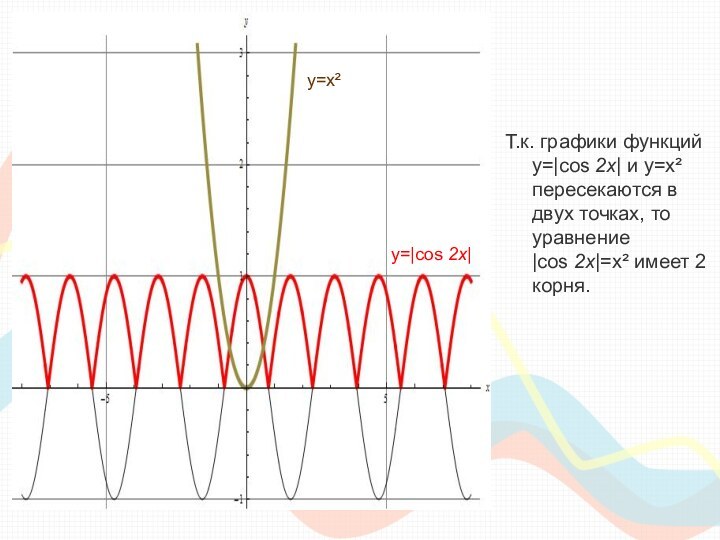
Вывод: в сборниках КИМ единого государственного экзамена по математике встречаются задания на использование знаний о различных преобразованиях графиков функций.

различных преобразований.
Задачи:
Исследовать взаимосвязь графика функции y=f(x) с графиками функций

y=|f(x)|, y=f(|x|) , y=f(kx), y=kf(x), y= -f(x), y=f(x)+b, y=f(x-a).
Рассмотреть задания на построение графиков функций с помощью преобразований.
Попробовать создать рисунок, используя исследуемые функции.
Узнать, есть ли более профессиональные и эффективные системы для построения графиков в декартовых системах координат кроме Excel и Calc, которые мы использовали для построения в прошлой работе.
Выявить в чём преимущества и недостатки этих компьютерных программ.

помощью преобразований графика исходной функции.

Объект – графики функций.

Предмет –

построение графиков сложных функций с помощью преобразования графика исходной функции.

Методы исследования: наблюдения, сравнения, анализ, обобщение, прогнозирование, знаковое моделирование.

часть, где х≥0, выполнить её симметрию относительно оси «оу»
y=|f(х)|
y=f(х)
Сохраняя

ту часть, где у≥0, выполнить симметрию относительно «ох» той части, где у<0

y=cos |x|
y=cos х

y= -cos x

y=cos х y=|cos x|

?

?

?

y= -cos x
Для того, чтобы из графика

функции y=cos x получить график функции y= - cos x , необходимо выполнить симметрию исходного графика относительно оси «ох».

?

y=cos х

y= -cos x

y=cos |x|
Для того, чтобы из графика функции

y=cos x получить график функции y=cos |x|, необходимо сохранить ту часть исходного графика, где х≥0, и выполнить её симметрию относительно «оу», а это и будет сам график y=cos x.

?

y=cos х

y=cos |x|

y=|cos x|
Для того, чтобы из графика функции y=cosx

получить график функции y=|cos x|, необходимо сохранить ту часть исходного графика, где у≥0, и выполнить симметрию относительно «ох» той части, где у<0.

?

y=cos х

y=|cos x|

y=|cos |x||
Для того, чтобы из графика функции y=cosx

получить график функции y=|cos|x||, необходимо сохранить ту часть исходного графика, где х≥0, и выполнить её симметрию относительно «оу», а затем сохранить ту часть получившеюся графика, где у≥0, и выполнить её симметрию относительно «ох» той части, где у<0.

?

y=cos х

y=cos |х|

y=|cos |х||

y=cos х

y=cos |х|

y=|cos |х||

y=cos 3x
y=cos 3x

График этой функции проходит через точки:

?

y=cos 3x
Вывод: Для того, чтобы из графика функции

y=cosx получить график функции y=cos 3x, необходимо сжать исходный график в 3 раза вдоль «ох».

?

y=cos х

y=cos 3x

y=cos x/3
y=cos x/3

График этой функции проходит через точки:

?

y=cos x/3
Вывод: Для того, чтобы из графика функции

y=cos x получить график функции y=cos x/3, необходимо выполнить растяжение исходного графика в 3 раза вдоль оси «ох».

?

y=cos х

y=cos x/3

y=3cos x
y=3cos x

График проходит через точки:
?

y=3cos x
Вывод: Для того, чтобы из графика функции

y=cos x получить график функции y=3cos x, необходимо растянуть исходный график в 3 раза вдоль оси «оу».

?

y=cos х

y=3cos x

y=cos(x+2)
y=cos(x+2)

Графиком является косинусоида, проходящая через точки:
?

y=cos(x+2)
Вывод: Для того, чтобы из графика функции y=cosx

получить график функции y=cos(x+2) , необходимо сдвинуть исходный график вдоль оси «ох» на 2 единицы влево.

?

y=cos х

y=cos(x+2)

y=cosx-3
y=cosx-3


Графиком является косинусоида, проходящая через точки:

?

y=cosx-3
Вывод: Для того, чтобы из графика функции y=cosx

получить график функции y=cos x -3, необходимо сдвинуть исходный график вдоль оси «оу» на 3 единицы вниз.

?

её симметрию относительно оси «оу»
y=f(x)
y=|f(x)|
Сохраняя ту часть, где у≥0,

выполнить симметрию относительно оси «ох» той части, где у<0

y=f(x)

y=f(kx)

Если k>1, то сжатие исходного графика в k раз вдоль оси «ох», если 0

y=f(x)

y=kf(x)

Если k>1, то растяжение исходного графика в k раз вдоль оси «оу», если 0

y=f(x)

y= -f(x)

Симметрия исходного графика относительно оси «ох»

y=f(x)

y=f(x-a)

Сдвиг вдоль оси «ох», если а≥0, то на а единиц вправо, если а<0, то на а единиц влево

y=f(x)

y=f(x)+b

Сдвиг вдоль оси «оу», если b≥0, то на b единиц вверх, если b<0, то на b единиц вниз

чтобы из графика функции

получить график функции необходимо растянуть исходный график в 4 раза вдоль оси «оу».

Исследование количества корней уравнения:

y=a

1.

Графиком является косинусоида, проходящая через точки:

2. у=а – линейная функция.
Графиком является прямая, параллельная оси «ох» и проходящая через точки (2;а) и (0;а).

при
б) Уравнение 4cos x=a не имеет корней при
y=4cos

x

y=6

y=4

y=1

y=-4

y=-6

y=cos 2x

y=|cos 2x|
Мы знаем, что для того, чтобы из графика функции y=cos x получить график функции y=cos 2x, необходимо сжать исходный график в 2 раза вдоль оси «ох», а затем, чтобы получить график функции y=|cos 2x|, необходимо сохранить ту часть графика, где у≥0, и выполнить симметрию относительно оси «ох» той части, где у<0.
y=cos x
Графиком является косинусоида, проходящая через точки:




y=x² - квадратичная функция.
Графиком является парабола, ветви которой направлены вверх.
(0;0) – вершина параболы.
«оу» - ось симметрии параболы.

y=|cos 2x|
y=x²

в двух точках, то уравнение |cos 2x|=x² имеет 2

корня.

y=|cos 2x|

y=x²

с помощью различных преобразований.

Задачи выполнены, мы исследовали взаимосвязь графика

функции y=f(x) с графиками функций y=|f(x)|, y=f(|x|) , y=f(kx), y=kf(x), y= -f(x), y=f(x)+b, y=f(x-a),научились строить эти графики, рассмотрели задания с применением таких функций, построили лицо мушкетёра, используя исследуемые функции, выяснили с помощью каких программных средств кроме Excel и Calc можно строить графики функций, выявили, в чём их преимущества и недостатки.

Теперь мы знаем, что для построения графиков используется не только Microsoft Office Excel и Open Office Calc, но есть и другие программы, не только не уступающие по возможностям этим программам, но и превышающие их, например,Wolfram Mathematica.

строить графики сложных функций с помощью преобразований графика исходной

функции, и если встретятся задания с применением этих функций, то мы будем знать, как они выполняются.

Использовать эти результаты можно при решении заданий единого государственного экзамена.