Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Подготовка к ОГЭ по математике

Содержание

При каких положительных значениях  прямая y=Kx-4  имеет с параболой y=x-3x  ровно одну общую точку? Найдите координаты этой точки и постройте данные графики в одной системе координат.
Функции и их свойстваЗадача 1 При каких положительных значениях  прямая y=Kx-4  имеет с параболой y=x-3x  ровно одну общую точку? Найдите Найдём абсциссы точек пересечения:Графики функций, будут иметь ровно одну точку пересечения, если По условию  поэтому нам подходит значение Подставив параметр  в уравнение, найдём  координату точки пересечения этих функ­ций: Теперь, зная   можем построить графики обеих функций Ответ:   координаты точки: (2; −2). 1. В треугольнике ABC известны длины сторон AB = 8, AC = 64, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная Проведём построения как показано на рисунке. Угол  ABE — вписанный и опирается на Угол  ECA  — вписанный и опирается на диаметр, следовательно, он прямой. Рассмотрим Ответ: 63.
Слайды презентации

Слайд 2 При каких положительных значениях  прямая y=Kx-4  имеет с параболой y=x-3x  ровно

При каких положительных значениях  прямая y=Kx-4  имеет с параболой y=x-3x  ровно одну общую точку?

одну общую точку? Найдите координаты этой точки и постройте

данные графики в одной системе координат.

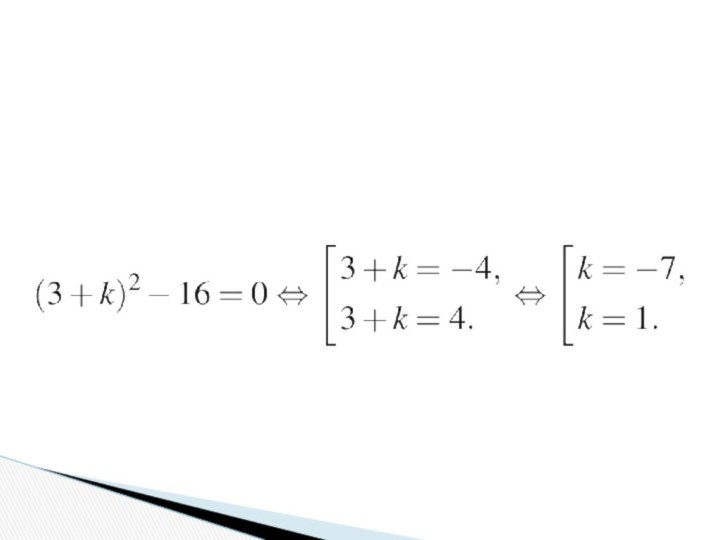
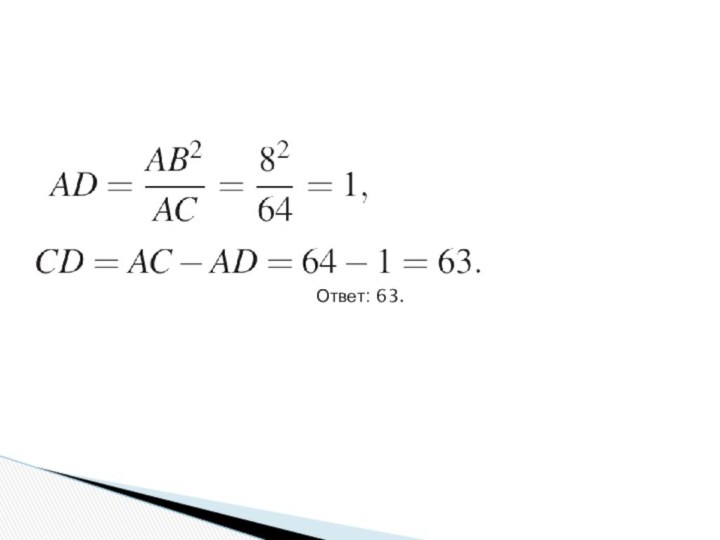
Слайд 3 Найдём абсциссы точек пересечения:
Графики функций, будут иметь ровно

Найдём абсциссы точек пересечения:Графики функций, будут иметь ровно одну точку пересечения,

одну точку пересечения, если это уравнение имеет ровно одно

решение. То есть, если дискриминант этого квадратного уравнения будет равен нулю.
 

Слайд 4

Слайд 5 По условию  поэтому нам подходит значение 
Подставив параметр  в уравнение, найдём  координату

По условию  поэтому нам подходит значение Подставив параметр  в уравнение, найдём  координату точки пересечения этих функ­ций:

точки пересечения этих функ­ций:


Слайд 6
Теперь, зная   можем построить графики обеих функций

Теперь, зная   можем построить графики обеих функций

Слайд 7 Ответ:   координаты точки: (2; −2).

Ответ:   координаты точки: (2; −2).

Слайд 8 1. В треугольнике ABC известны длины сторон AB = 8, AC = 64, точка O — центр окружности, описанной

1. В треугольнике ABC известны длины сторон AB = 8, AC = 64, точка O — центр окружности, описанной около треугольника ABC. Прямая BD,

около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найдите CD.
Задача

2

Слайд 9 Проведём построения как показано на рисунке. Угол  ABE —

Проведём построения как показано на рисунке. Угол  ABE — вписанный и опирается

вписанный и опирается на диаметр, значит, угол  ABE — прямой. Рассмотрим

треугольники AEB и ABF они прямоугольные, угол BAE — общий, следовательно, эти треугольники подобны. Откуда:

Слайд 10 Угол  ECA  — вписанный и опирается на диаметр,

Угол  ECA  — вписанный и опирается на диаметр, следовательно, он прямой.


следовательно, он прямой.
Рассмотрим треугольники  AEC  и  AFD
 они прямоугольные,

угол  FAD
— общий, следовательно,
эти треугольники подобны. Откуда
  • Имя файла: prezentatsiya-podgotovka-k-oge-po-matematike.pptx
  • Количество просмотров: 95
  • Количество скачиваний: 0
- Предыдущая Презентация Усиление королевской власти7 класс
Следующая - Презентация по русскому языку Знаки препинания при причастном обороте 6 класс

Похожие презентации

2 сыныпқа арналған презентацияҚұн Сан Баға 2 сыныпқа арналған презентацияҚұн Сан Баға 176
Готовимся к контрольной работе Готовимся к контрольной работе 116
Полезные функции Matlab’a Полезные функции Matlab’a 155
Трёхзначные числа (математика, 2 класс, УМК Гармония) презентация к уроку по математике (2 класс) по теме Трёхзначные числа (математика, 2 класс, УМК Гармония) презентация к уроку по математике (2 класс) по теме 112
chislovye vyrazheniya chislovye vyrazheniya 103
Решение задач 3 класс презентация к уроку по математике (3 класс) Решение задач 3 класс презентация к уроку по математике (3 класс) 112
Математические модели сложных систем Математические модели сложных систем 135
Готовимся к ОГЭ по математике, решение задания №24 Готовимся к ОГЭ по математике, решение задания №24 170
тренажер по математике тренажер по математике 132
Умение читать свойства функции по графику Умение читать свойства функции по графику 82
Технологическая карта урока математики в 3 кл. Сантиметр и миллиметр план-конспект занятия по математике (3 класс) Технологическая карта урока математики в 3 кл. Сантиметр и миллиметр план-конспект занятия по математике (3 класс) 153
Геометрические преобразования и паркеты Геометрические преобразования и паркеты 124
БЮДЖЕТ СЕМЬИ НА МАТЕМАТИЧЕСКОМ ЯЗЫКЕ Секция: Математики БЮДЖЕТ СЕМЬИ НА МАТЕМАТИЧЕСКОМ ЯЗЫКЕ Секция: Математики 162
Графики Графики 130
Путешествие в прошлое города Воркута Путешествие в прошлое города Воркута 119
Уменьшаемое,вычитаемое, разность. план-конспект урока по математике (1 класс) Уменьшаемое,вычитаемое, разность. план-конспект урока по математике (1 класс) 97
Уголок экспериментирования презентация по математике Уголок экспериментирования презентация по математике 124
Применение свойств квадратичной функции Применение свойств квадратичной функции 125
ЕГЭ по математике 2011 ЕГЭ по математике 2011 111
Арифметические действия с натуральными числами Арифметические действия с натуральными числами 114
Решение уравнений, содержащих переменную под знаком модуля Решение уравнений, содержащих переменную под знаком модуля 106
Нелинейные модели парной регрессии Нелинейные модели парной регрессии 151
Презентация по геометрии на тему Метод параллельного проектирования Презентация по геометрии на тему Метод параллельного проектирования 141
Презентация Вычитание числа 4 Презентация Вычитание числа 4 94
История счёта История счёта 161
Вставь пропущенные цифры 6-7 лет презентация к уроку по математике (подготовительная группа) по теме Вставь пропущенные цифры 6-7 лет презентация к уроку по математике (подготовительная группа) по теме 135
Решение старинных задач из Арифметики Л.Ф. Магницкого Решение старинных задач из Арифметики Л.Ф. Магницкого 143
Презентация урока по математике 1 класс презентация к уроку по математике (1 класс) Презентация урока по математике 1 класс презентация к уроку по математике (1 класс) 129
Умножение обыкновенных дробей Умножение обыкновенных дробей 117
Знакомство с многоугольниками.Математика 1 класс. презентация к уроку по математике (1 класс) Знакомство с многоугольниками.Математика 1 класс. презентация к уроку по математике (1 класс) 120