- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Приближенное значение величины. Абсолютная и относительная погрешности
Содержание
- 2. Приближенным числом а называется число, незначительно отличающееся
- 3. Если а А – приближенным значением по избытку
- 5. Пример 1. Пусть А = 784,2737,а, =
- 7. Пример 5. Пусть при измерениикниги и длины
- 9. Пример 8. РешениеОтвет: измерение y произведено более точно
- 10. Погрешности арифметических действий
- 11. Если c=a+b, или c=a-b, c*=a*+b* c*=a*-b*, то
- 12. Если u=ab, или
- 13. Относительные погрешности произведения и частного:
- 14. , Если u=ab, тоЕсли v=a/b, то
- 15. Пример 1Вычислите сумму и разность приближённых чисел 0,123 и 0,526.также равна 0,001.
- 16. Пример 2Измерения цилиндрической полой изнутри трубы показали, что
- 17. Позиционная запись числа: или a*=± Первая слева
- 18. Цифра aj называется верной, если , т.е.
- 19. Правило. За абсолютную погрешность приближенного числа с
- 20. Абсолютная и относительная погрешность вычисления
- 21. Абсолютная и относительная погрешность вычисления функции нескольких переменных.
- 22. Итак, для оценки погрешности мы получили следующие
- 23. Приближенные решения алгебраических и трансцендентных уравнений
- 24. План лекции1.Алгебраические и трансцендентныеуравнения2.Графический метод решения уравнений3.Отделение корней
- 25. φ(x)=g(x) (1)f(x)=0(2)- корень уравнения, еслиf( )=0
- 26. x -10sin x = 02x - 2cos
- 27. ✍Задача численного нахождения корней уравнения состоит из двух этапов:отделение корнейуточнение корней
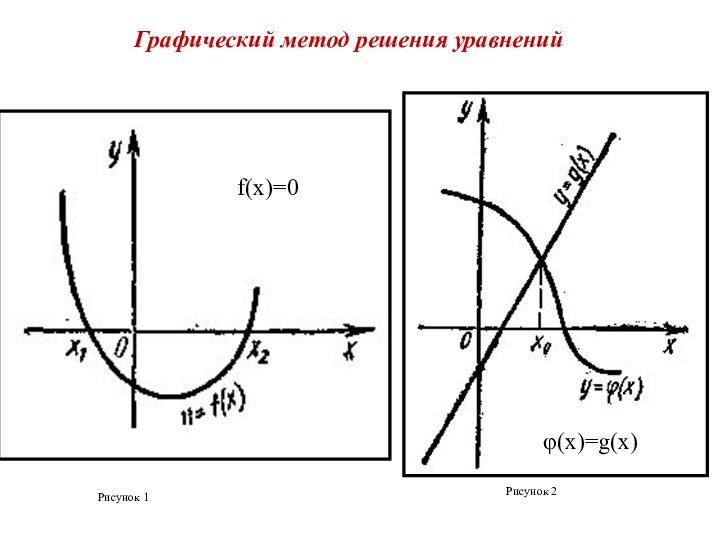
- 28. Рисунок 1 Рисунок 2Графический метод решения уравнений φ(x)=g(x)f(x)=0
- 29. Пример 1. Решить графически уравнение х3 -
- 30. Пример 2. Решить уравнение lg х -
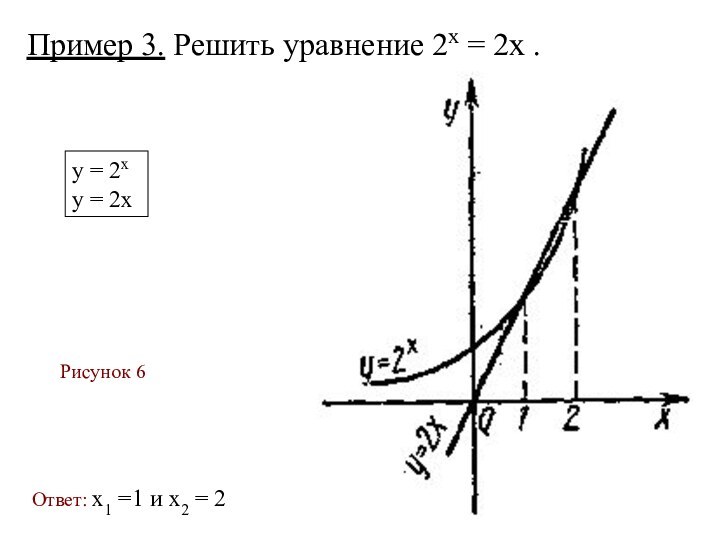
- 31. Пример 3. Решить уравнение 2х = 2х
- 32. Отделение корней ✍Корень
- 33. Аналитический метод отделения корней 1) Если непрерывная
- 34. Скачать презентацию
- 35. Похожие презентации
Приближенным числом а называется число, незначительно отличающееся от точного числа А и заменяющее последнее в вычислениях



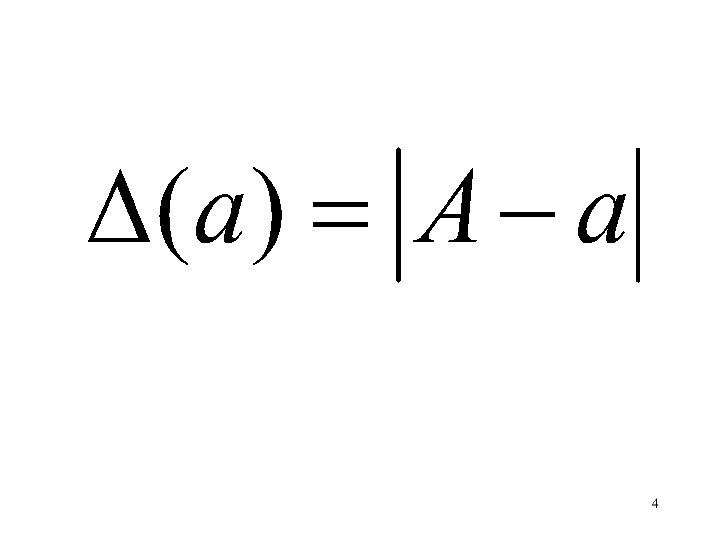

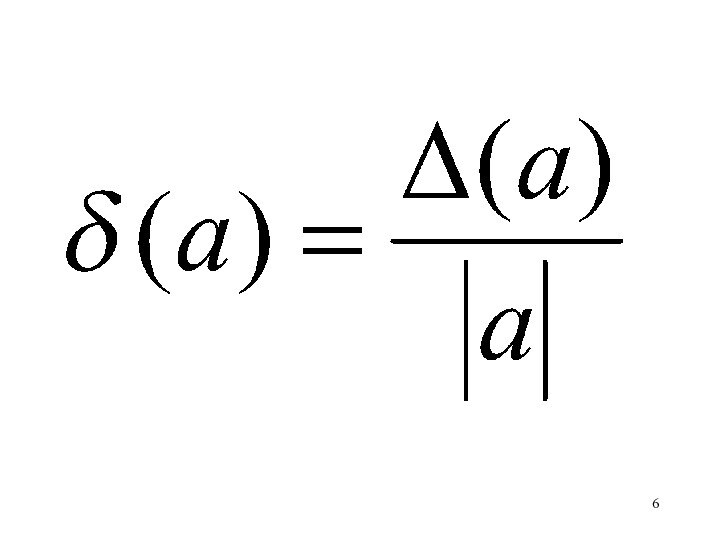

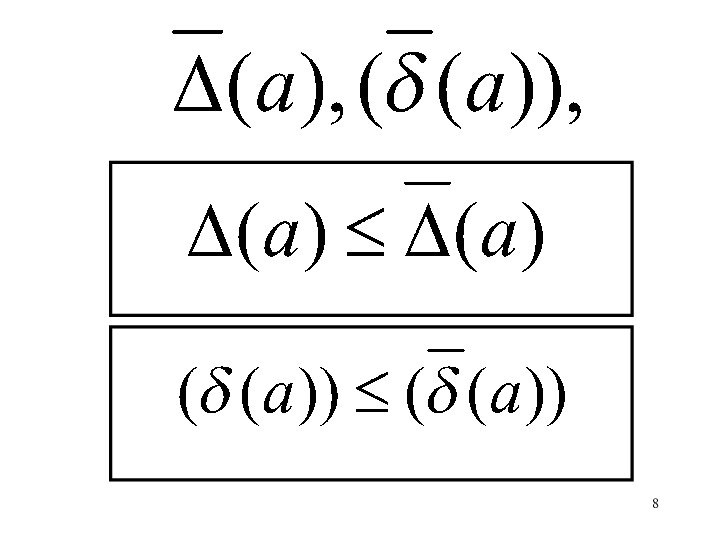


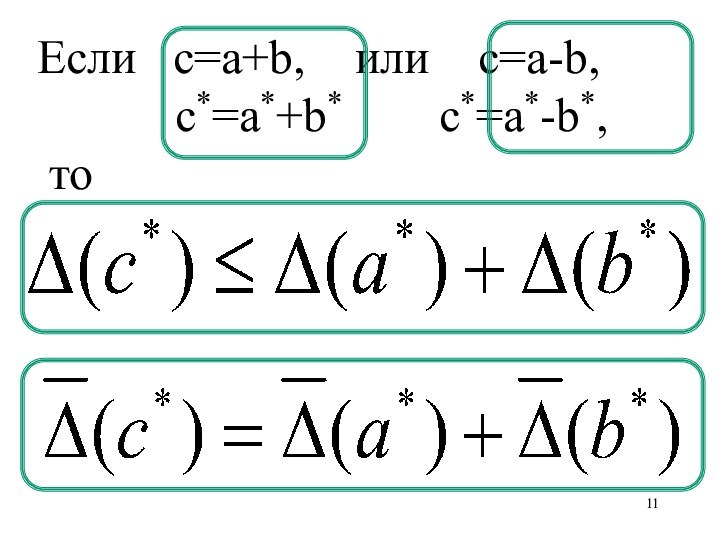


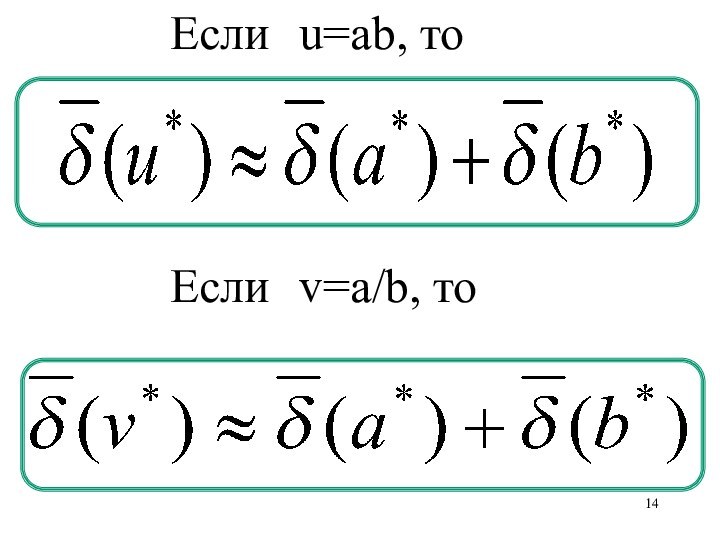














Слайд 5
Пример 1. Пусть А = 784,2737,
а, = 784,274.
Найти абсолютную
погрешность приближенного
числа
Δа = | А-а| =
|784,2737—784,274|
= 0,0003
Решение
Ответ: 0,0003
Слайд 7
Пример 5. Пусть при измерении
книги и длины стола
были
получены результаты:
l1 = 28,4 ±0,1 (см) и
l2
= 110,3 ±0,1 (см). Решение
Ответ: измерение стола точнее
Слайд 16
Пример 2
Измерения
цилиндрической полой изнутри трубы
показали, что ее
внешний радиус равен
100 см, а внутренний радиус –
98 см.Чему равна толщина стенок трубы?
Вычислите относительную погрешность
произведенных расчетов.
Слайд 17
Позиционная запись числа:
или
a*=±
Первая слева цифра
данного числа, отличная от нуля, и все расположенные за
ней цифры называются значащимиНапример, числа 25,047 и –0,00259 имеют соответственно
5 и 3 значащих цифры.
Слайд 18
Цифра aj называется верной,
если
, т.е.
абсолютная
погрешность числа a*
не превосходит одной единицы
соответствующего разряда
десятичного числа Например, a*=0,03045 (a*)=0,000003
Последнюю верную цифру или все верные цифры
обычно подчеркивают
Слайд 19
Правило.
За абсолютную погрешность
приближенного числа с
известными
верными значащими
цифрами принимается
половина единицы того разряда,
где
находится последняя верная цифра.
Слайд 20 Абсолютная и относительная погрешность вычисления функции
одной переменной
Теорема. Предельная абсолютная погрешность вычисления функции равна произведению
абсолютной величины ее производной на предельную абсолютную погрешность аргумента. где
Слайд 22 Итак, для оценки погрешности мы получили следующие простые
правила:
При сложении и вычитании абсолютные погрешности складываются;
При умножении и
делении относительные погрешности складываются; При возведении в степень относительные погрешности умножаются на абсолютную величину показателя степени;
Слайд 24
План лекции
1.Алгебраические и трансцендентные
уравнения
2.Графический метод решения уравнений
3.Отделение корней
Слайд 26
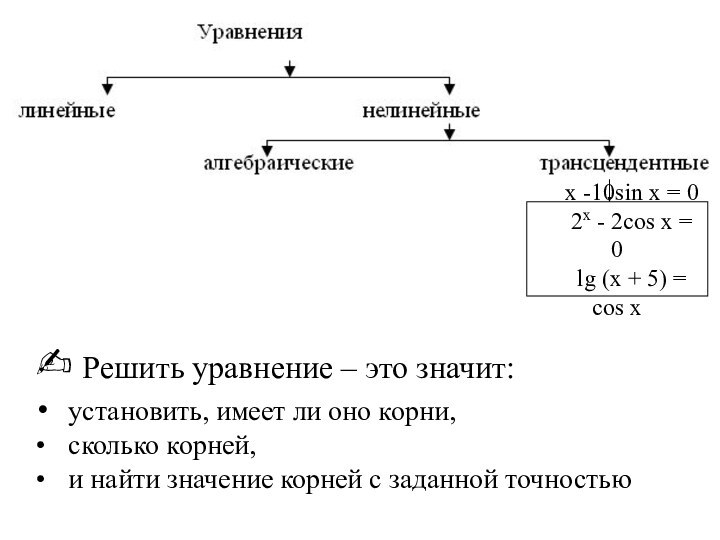
x -10sin x = 0
2x - 2cos x
= 0
lg (x + 5) = cos x
✍ Решить
уравнение – это значит:установить, имеет ли оно корни,
сколько корней,
и найти значение корней с заданной точностью
Слайд 27
✍Задача численного нахождения корней уравнения
состоит из двух
этапов:
отделение корней
уточнение корней
Слайд 29
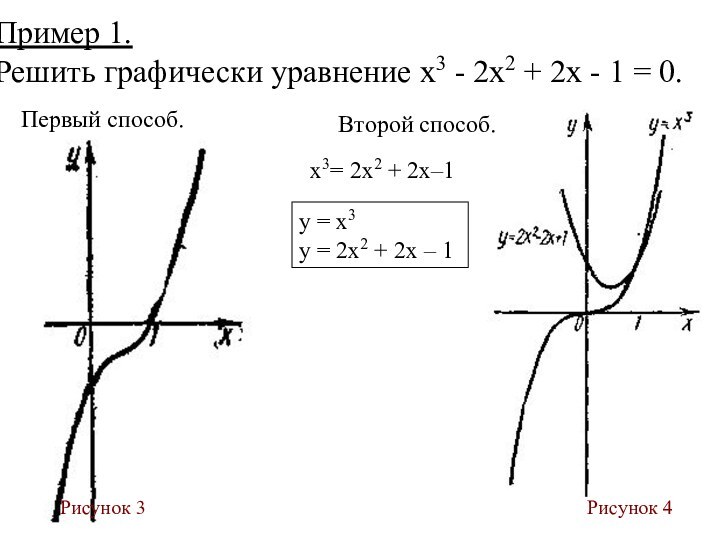
Пример 1.
Решить графически уравнение х3 - 2x2
+ 2х - 1 = 0.
Рисунок 3
Рисунок
4Первый способ.
Второй способ.
х3= 2x2 + 2х–1
у = х3
у = 2x2 + 2х – 1
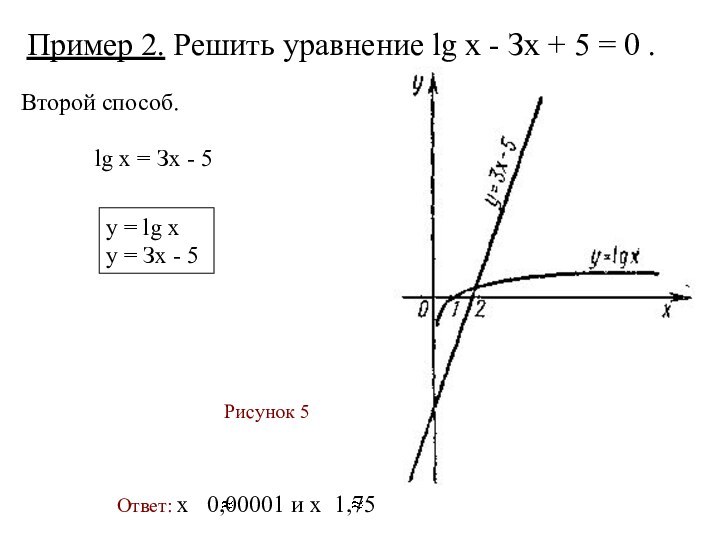
Слайд 30 Пример 2. Решить уравнение lg х - Зх
+ 5 = 0 .
Рисунок 5
Второй способ.
lg
х = Зх - 5 у = lg х
у = Зх - 5
Ответ: x 0,00001 и x 1,75
Слайд 32
Отделение корней
✍Корень уравнения
f(х) = 0 считается
отделенным на отрезке [a,b], если
на этомотрезке уравнение f(х) = 0 не имеет
других корней
Слайд 33
Аналитический метод отделения корней
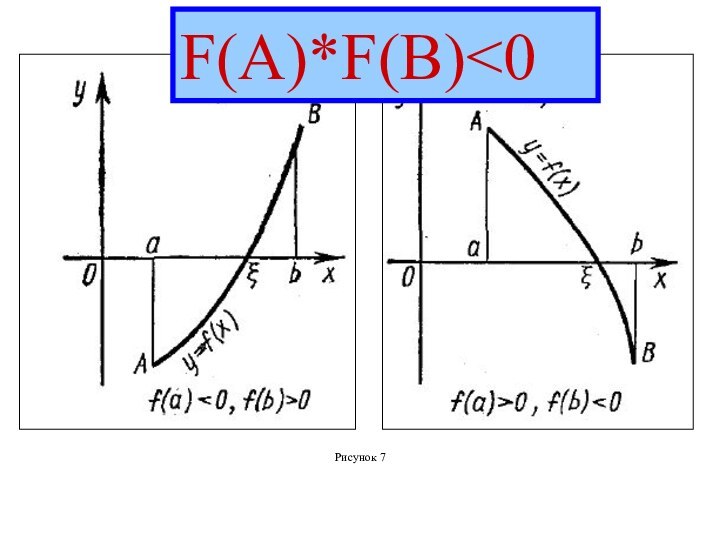
1) Если непрерывная на
отрезке
функция F(x) принимает на его концах
значения разных
знаков, то уравнениеF(x)=0
имеет на этом отрезке, по меньшей мере,
один корень
2) Если функция F(x) к тому же еще и
строго монотонна, то корень на отрезке
единственный