функции;
Достаточный признак убывания функции;
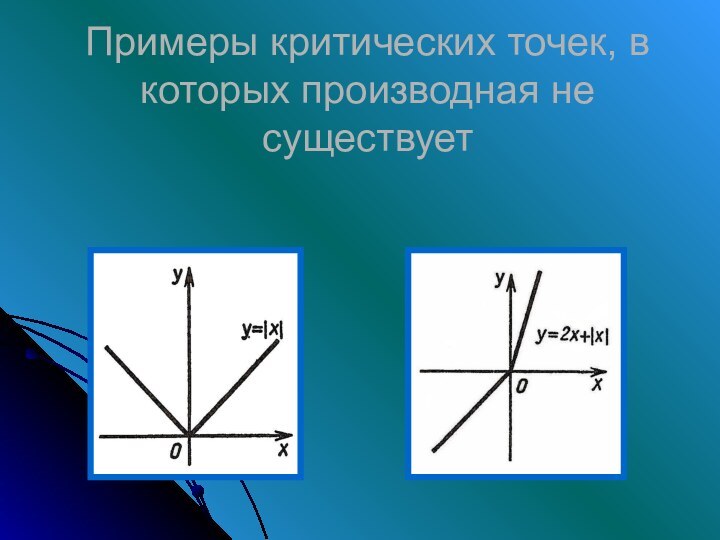
Критические точки функции:
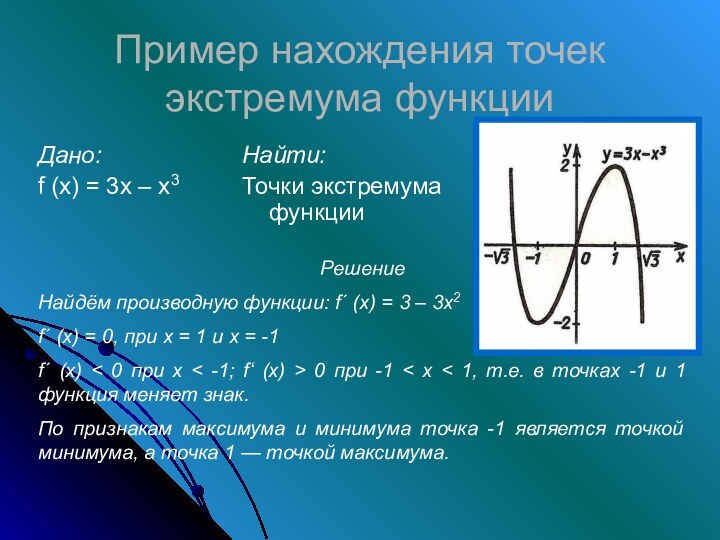
Необходимое условие экстремума;
Признак максимума
функции;Признак минимума функции.