- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Производная и её применение
Содержание
- 2. Цель работы:Закрепление изученного материала по теме «Производная» и ознакомление с её прикладной частью.
- 3. План работы:1.Исследование функции на
- 4. Определение производной Производной данной функции
- 5. . Будем считать, что рассматриваемая функция y=f(x)
- 6. Решение: Чтобы применить признаки возрастания
- 11. В ΔASC ОC1 - средняя линия (значит
- 15. Если функция f имеет положительную (отрицательную) производную
- 16. Скачать презентацию
- 17. Похожие презентации















Слайд 2
Цель работы:
Закрепление изученного материала по теме «Производная» и
ознакомление с её прикладной частью.
Слайд 3
План работы:
1.Исследование функции на монотонность
2.Касательная
к графику.
3.Наибольшие, наименьшие значения функций.
4.Нахождение дифференциала для приближенных
вычислений.5.Доказательство неравенств.
Слайд 4
Определение производной
Производной данной функции в
точке х называется предел отношения приращения этой функции к
приращению аргумента в точке х, когда приращение аргумента стремится к нулю.
Слайд 5
.
Будем считать, что рассматриваемая функция y=f(x) определена
и дифференцируема в каждой точке отрезка a ≤ x
≤ b.функция f(x) возрастает (или убывает) в промежутке a
Пример. Определить промежутки возрастания и убывания функции: у = х3 — х2 — 8х + 2.
Слайд 6 Решение: Чтобы применить признаки возрастания и
убывания функции, найдем производную данной функции и определим значения
х, при которых она положительна или отрицательна:у' = Зх2 — 2х — 8.
Корни трехчлена: x1= - 4/3, x2=2.
Отсюда:
у' =3(х+4/3)(х-2).
возрастает убывает возрастает
+ -4/3 - 2 +
Ответ: функция возрастает в промежутках
- ∞ < x < -4/3 и 2 < x < + ∞ и убывает в промежутке — 4/3 < х <2.
Слайд 7
Вообразим, что на кривой АВ точка М неограниченно приближается к неподвижной точке С, секущая СМ при этом вращается вокруг точки С. Может случиться, что, независимо от того, будет ли точка М приближаться к С в направлении от A к С или от В к С (на черт точка M'), существует одна и та же прямая СТ — предельное положение секущей СМ.
Слайд 8
Определение. Прямая СТ, предельное положение секущей СМ, называется касательной к кривой в точке С.
Точка С называется точкой прикосновения или касания.
Если к линии y=f(x) в точке х имеется касательная, непараллельная Оу, то угловой коэффициент касательной равен значению производной f '(х), в точке х.
Если функция y=f(x) имеет определенную производную в точке х, то:
1) в этой точке имеется касательная к графику функции,
2) угловой коэффициент ее равен значению производной f '(x) в точке х.
Слайд 9
∙
Задача . Найдите площадь треугольника AMB, если A и B — точки пересечения с осью OX касательных, проведенных к графику y = (9—x2)/6 из точки M(4;3).
Решение.
укас =y(x0)+у’(x0)(x—x0); y’(x0) = 1/6 ∙ (-2x) = -x/3; т.к. укас проходит через M(4;3), то
3 = (9—x02) — (4—x0) ∙ x0/3
x02—8 x0—9 = 0;
Д/4 = 16 + 9 = 25; x0 = 9; x0 = -1
укас1 = - 12 - 3 ∙ ( x – 9) = -3x + 15
укас2 = 4/3 + 1/3 ∙ (x + 1) = 1/3x + 5/3
5 А
A(5;0); B(-5;0);
AM = 2√ 5 (ед.); М
AB = 10 (ед.); 3
BM = 4√5 (ед.);
4
р/2 = 3√5 +5
S = √ (3√5 +5) ∙ (√5 +5 ) ∙ (5 - √5 ) ∙ (3 √5 -5)
S = 20 ( кв.ед. ). В
Ответ: 20 кв.ед.
Слайд 10
Задача . В прямоугольном параллелепипеде ABCDA1B1C1D1 с ребрами CD = 24, AD= 6 и
DD1 =4 проведена плоскость через центр симметрии грани A1B1C1D1 , вершину А и точку Р, лежащую на ребре DC. Какую наименьшую площадь может иметь сечение параллелепипеда этой плоскостью? На какие части делит точка P ребро DC в этом случае?
. 3.Наибольшие, наименьшие значения функций
Решение.
Проведем плоскость и построим сечение (рис.).
АО АA1C1С - линия, принадлежащая данной плоскости. Продолжим АО до пересечения с CC1 в точке S. Тогда SP - линия пересечения грани DD1C1C и данной плоскости, а сечение ANMP - параллелограмм. Sсеч = SAMNP = SK ∙AP/2 SK/2— высота параллелограмма ANMP.
Слайд 11
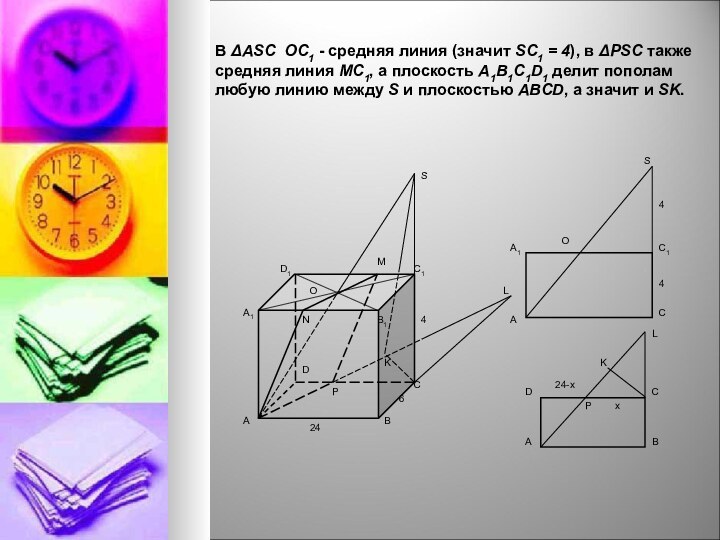
В ΔASC ОC1 - средняя линия (значит SC1
= 4), в ΔPSC также средняя линия МC1, а
плоскость A1B1C1D1 делит пополам любую линию между S и плоскостью ABCD, а значит и SK.Слайд 12
Пусть PC = x; ΔCLP подобен
ΔDАРLC/AD = x/(24—x), LC = 6x/(24 – x).
Из ΔCLP: KC = (6x ∙x/(24—x))/(√(36x2/(24—x)2)+x2) =
= 6x/(√(36+ (24—x)2);
Из ΔSCK: SK = √SC2+ KC2 = √64+36x2/(36+(24—x)2) = 2√16+9x2/(36+(24—x)2) ;
Из ΔADP: AP = √36+(24—x)2;
Sсеч = AP∙SK/2 = 0,5∙(√36+(24—x)2) 2√16+9x2/(36+(24—x)2) =
=√16(36+(24—x)2)+9x2;
Если S’(x) = 0, то 18x+16 ∙2(24—x)(-1) = 0;
50x—768 = 0, x = 384/25 (это точка min);
Sсеч = 312;
DP = 24—384/25 = 216/25;
Ответ: 312 кв. ед.; DC- 384/25; 216/25.
Слайд 13
4.Нахождение дифференциала для
приближенных вычислений.
Определение. Дифференциалом (dy) функции y=f(x) называется произведение значения производной f '(х) на произвольное приращение ∆x аргумента х, т. е.
dy=f '(x)∙∆x
(I)
при достаточно малом ∆x
∆y ≈ dy =f '(х)∆x
Это означает, что при малых изменениях аргумента (от начального значения х) величину изменения функции y=f(x) можно приближенно считать пропорциональной величине изменения аргумента с коэффициентом пропорциональности, равным значению производной f '(x);
f(x+∆x) ≈ f(x) + f '(x) ∙ f(x+∆x) ≈ f(x) + f '(x) ∙ ∆x
Слайд 14
Пример:
Вычислить приближенно с помощью дифференциала.
.
В нашем случае:
,
,
.
Вычисляем:
;
,
.
Имеем:
.
Слайд 15 Если функция f имеет положительную (отрицательную) производную в
каждой точке некоторого промежутка, то она возрастает (убывает) на
этом промежутке. При нахождении промежутков монотонности нужно иметь в виду, что если функция возрастает (убывает) на интервале (a,b) и непрерывна в точках a и b, то она возрастает (убывает) на отрезке [a,b].5.Доказательство неравенств.
Для отыскания наибольших и наименьших значений f на отрезке [a,b] достаточно сравнить между собой значения f в точках a, b и в критических точках из отрезка [a,b].
Эти результаты применимы при решении многих элементарных задач, связанных с неравенствами.