Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Производная. Точки экстремума и перегиба. Возрастание и выпуклость функции

Содержание

Вогнутость функции Точки максимума Точки минимумаТочки перегиба Убывание функции Выпуклость функции СОДЕРЖАНИЕНули функцииy=f(x)Возрастаниефункции
ГБОУ СПО Петрозаводский лесотехнический техникум «Производная. Точки экстремума и перегиба. Возрастание и Вогнутость функции Точки максимума Точки минимумаТочки перегиба Убывание функции Выпуклость функции СОДЕРЖАНИЕНули функцииy=f(x)Возрастаниефункции 1. Возрастание функцииФункция y=f(x) называется возрастающей на промежутке, если при возрастании аргумента, 2. Убывание функцииФункция y=f(x) называется убывающей на промежутке, если при возрастании аргумента, 3. Точки максимумаТочка х = а называется точкой максимума функции y=f(x) если 4. Точки минимумаТочка х = а называется точкой минимума функции y=f(x) если 5. Выпуклость функцииФункция y=f(x) называется выпуклой на промежутке, если все точки графика функции расположены ниже касательной.y=f(x) 6. Вогнутость функцииФункция y=f(x) называется вогнутой на промежутке, если все точки графика функции расположены выше касательной.y=f(x)у”>0у”>0 7. Точки перегибаP1Точка Р называется точкой перегиба функции y=f(x) если при переходе 8. Нули функцииТочки, в которых график функции пересекает ось ОХ называются нулями Список литературы:Учебник: Богомолов, Н. В. Практические занятия по математике: учеб. пособие для
Слайды презентации

Слайд 2 Вогнутость
функции
Точки
максимума
Точки
минимума
Точки
перегиба
Убывание

Вогнутость функции Точки максимума Точки минимумаТочки перегиба Убывание функции Выпуклость функции СОДЕРЖАНИЕНули функцииy=f(x)Возрастаниефункции


функции
Выпуклость
функции
СОДЕРЖАНИЕ
Нули
функции
y=f(x)
Возрастание
функции

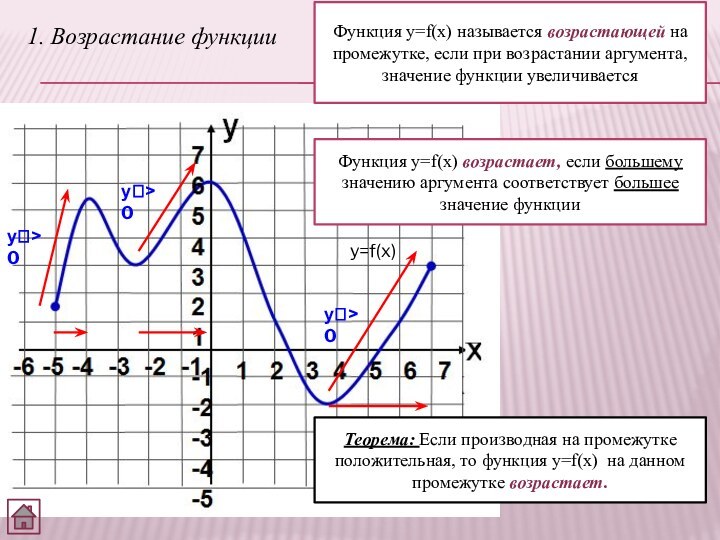
Слайд 3 1. Возрастание функции
Функция y=f(x) называется возрастающей на промежутке,

1. Возрастание функцииФункция y=f(x) называется возрастающей на промежутке, если при возрастании

если при возрастании аргумента, значение функции увеличивается
Функция y=f(x) возрастает,

если большему значению аргумента соответствует большее значение функции

Теорема: Если производная на промежутке положительная, то функция y=f(x) на данном промежутке возрастает.

y=f(x)

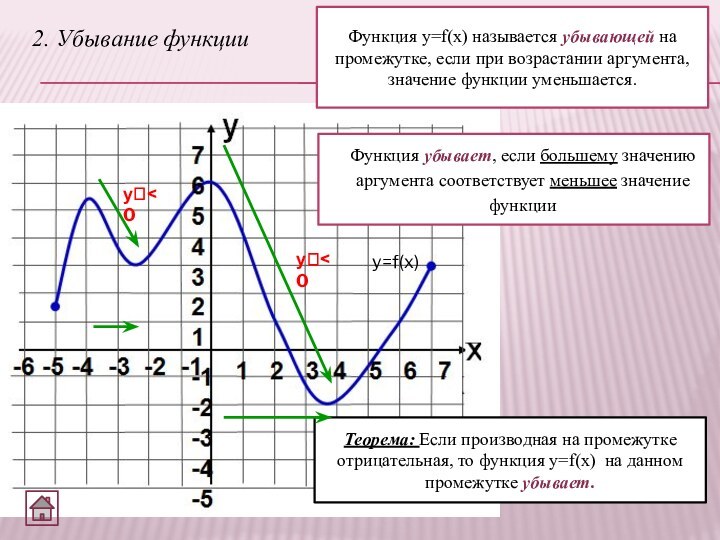
Слайд 4 2. Убывание функции
Функция y=f(x) называется убывающей на промежутке,

2. Убывание функцииФункция y=f(x) называется убывающей на промежутке, если при возрастании

если при возрастании аргумента, значение функции уменьшается.
Функция убывает, если

большему значению аргумента соответствует меньшее значение функции

Теорема: Если производная на промежутке отрицательная, то функция y=f(x) на данном промежутке убывает.

y=f(x)

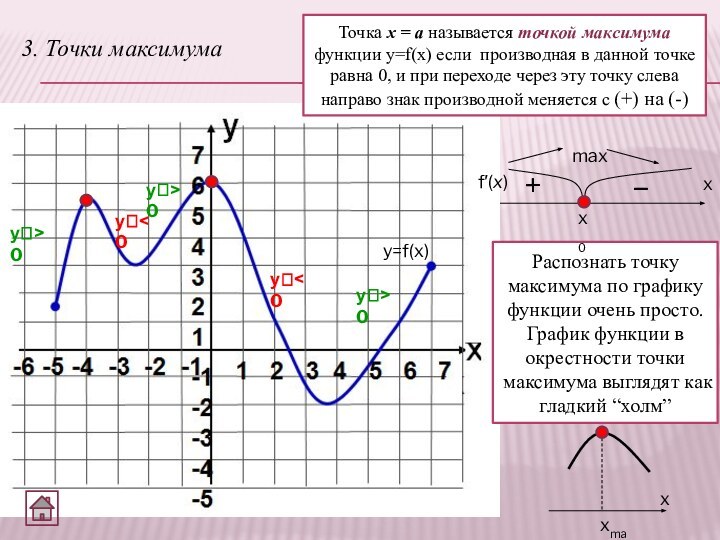
Слайд 5 3. Точки максимума
Точка х = а называется точкой

3. Точки максимумаТочка х = а называется точкой максимума функции y=f(x)

максимума функции y=f(x) если производная в данной точке равна

0, и при переходе через эту точку слева направо знак производной меняется с (+) на (-)

y=f(x)

Распознать точку максимума по графику функции очень просто. График функции в окрестности точки максимума выглядят как гладкий “холм”

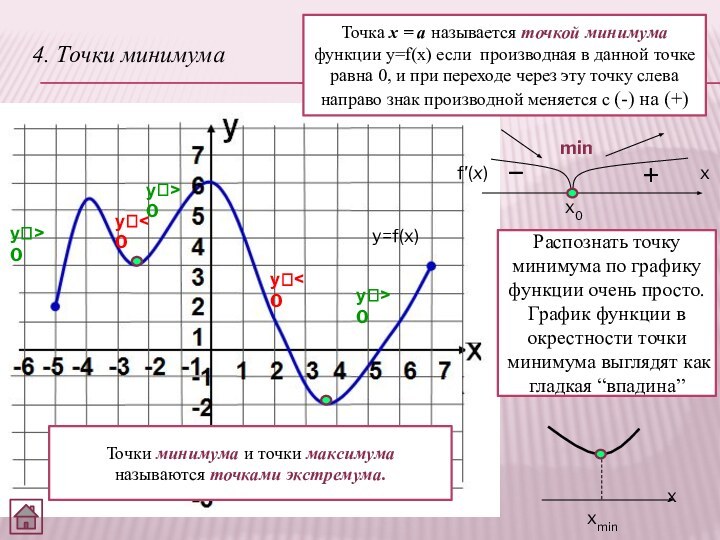
Слайд 6 4. Точки минимума
Точка х = а называется точкой

4. Точки минимумаТочка х = а называется точкой минимума функции y=f(x)

минимума функции y=f(x) если производная в данной точке равна

0, и при переходе через эту точку слева направо знак производной меняется с (-) на (+)

Точки минимума и точки максимума называются точками экстремума.

y=f(x)

Распознать точку минимума по графику функции очень просто. График функции в окрестности точки минимума выглядят как гладкая “впадина”

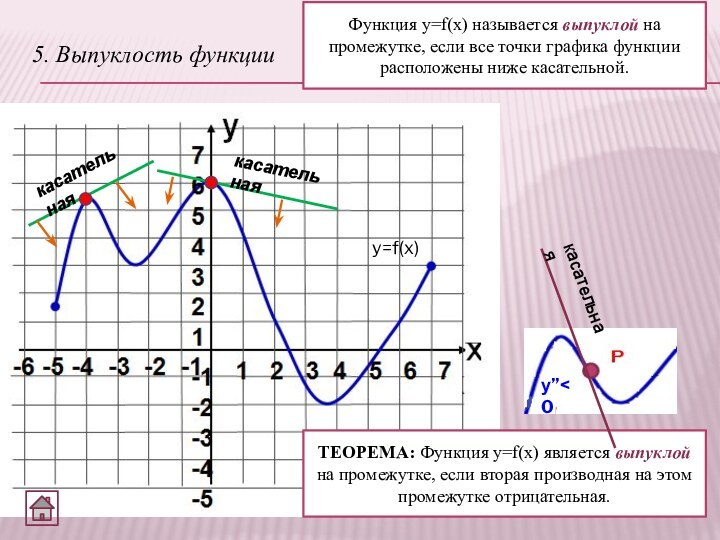
Слайд 7 5. Выпуклость функции
Функция y=f(x) называется выпуклой на промежутке,

5. Выпуклость функцииФункция y=f(x) называется выпуклой на промежутке, если все точки графика функции расположены ниже касательной.y=f(x)

если все точки графика функции расположены ниже касательной.
y=f(x)

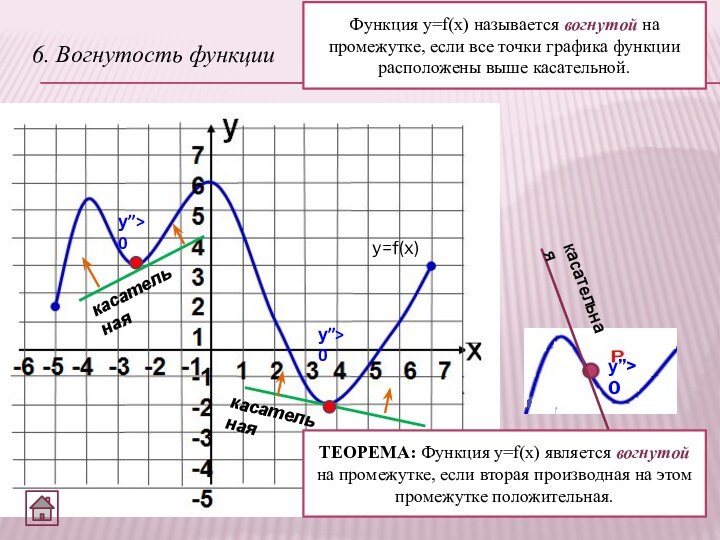
Слайд 8 6. Вогнутость функции
Функция y=f(x) называется вогнутой на промежутке,

6. Вогнутость функцииФункция y=f(x) называется вогнутой на промежутке, если все точки графика функции расположены выше касательной.y=f(x)у”>0у”>0

если все точки графика функции расположены выше касательной.
y=f(x)
у”>0
у”>0

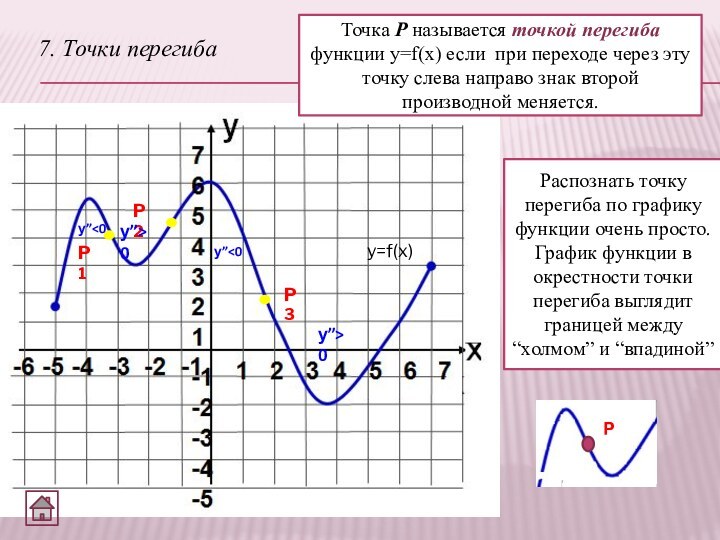
Слайд 9 7. Точки перегиба
P1

Точка Р называется точкой перегиба функции

7. Точки перегибаP1Точка Р называется точкой перегиба функции y=f(x) если при

y=f(x) если при переходе через эту точку слева направо

знак второй производной меняется.

y=f(x)

Распознать точку перегиба по графику функции очень просто. График функции в окрестности точки перегиба выглядит границей между “холмом” и “впадиной”

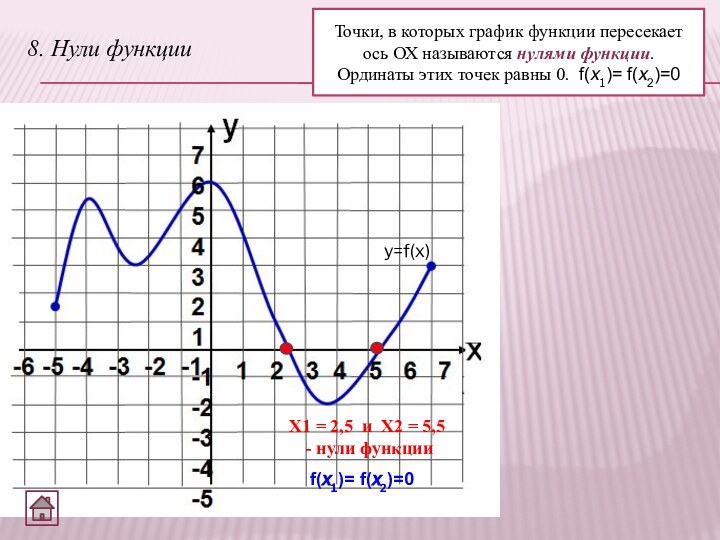
Слайд 10 8. Нули функции
Точки, в которых график функции пересекает

8. Нули функцииТочки, в которых график функции пересекает ось ОХ называются

ось ОХ называются нулями функции.
Ординаты этих точек равны 0.

f(x1)= f(x2)=0

y=f(x)

  • Имя файла: proizvodnaya-tochki-ekstremuma-i-peregiba-vozrastanie-i-vypuklost-funktsii.pptx
  • Количество просмотров: 107
  • Количество скачиваний: 1
- Предыдущая Математический КВН
Следующая - ВЕКТОР

Похожие презентации

Старинные задачи Старинные задачи 103
Повторение и обобщение изученного материала. Математика 3 класс. презентация к уроку по математике (3 класс) Повторение и обобщение изученного материала. Математика 3 класс. презентация к уроку по математике (3 класс) 158
Математическая игра для 5-6 классов Математика кругом Математическая игра для 5-6 классов Математика кругом 137
презентация игры ФЭМП Помоги котику презентация к уроку по математике (старшая группа) презентация игры ФЭМП Помоги котику презентация к уроку по математике (старшая группа) 131
Свойство биссектрисы угла треугольника Свойство биссектрисы угла треугольника 127
Устный счёт в пределах 100. презентация урока для интерактивной доски по математике (2 класс) по теме Устный счёт в пределах 100. презентация урока для интерактивной доски по математике (2 класс) по теме 112
ЭОР. Тест Сложение и вычитание круглых чисел выполнен с использованием программы Microsoft Power Point тест по математике (2 класс) по теме ЭОР. Тест Сложение и вычитание круглых чисел выполнен с использованием программы Microsoft Power Point тест по математике (2 класс) по теме 134
Подготовка к ЕГЭ 2012. Диаграммы и графики Подготовка к ЕГЭ 2012. Диаграммы и графики 155
Мой кабинет-моя лаборатория Мой кабинет-моя лаборатория 109
Экология и математика Экология и математика 167
Угол. Виды углов. 5 класс Угол. Виды углов. 5 класс 121
Астрономия на координатной плоскости Астрономия на координатной плоскости 114
Конспект урока математики в 3 классе Решение уравнений вида х : 5 = 6 + 9. план-конспект урока по математике (3 класс) по теме Конспект урока математики в 3 классе Решение уравнений вида х : 5 = 6 + 9. план-конспект урока по математике (3 класс) по теме 108
состав числа 5 состав числа 5 51
Виды уравнений Виды уравнений 108
Сложение и вычитание десятичных дробей 5 класс Сложение и вычитание десятичных дробей 5 класс 129
Прогрессии Прогрессии 153
Измерение отрезков Измерение отрезков 108
Масштаб карты Масштаб карты 120
Презентация по геометрии на тему Отрезок и луч Презентация по геометрии на тему Отрезок и луч 121
Первый признак равенства треугольников Первый признак равенства треугольников 87
Презентация по предметной недели математики вначальной школе игра Умники и умницы Презентация по предметной недели математики вначальной школе игра Умники и умницы 117
Задачи на уменьшение и увеличение числа план-конспект урока по математике (1 класс) по теме Задачи на уменьшение и увеличение числа план-конспект урока по математике (1 класс) по теме 167
Величины массы Величины массы 128
Знакомство с многоугольниками Знакомство с многоугольниками 105
Путешествие в страну Тик-Так учебно-методическое пособие по математике (подготовительная группа) Путешествие в страну Тик-Так учебно-методическое пособие по математике (подготовительная группа) 120
Электронное пособие по математике для учащихся 2 класса. Тема: Миллиметр презентация к уроку по математике (2 класс) Электронное пособие по математике для учащихся 2 класса. Тема: Миллиметр презентация к уроку по математике (2 класс) 159
Задания с самопроверкой Проценты и дроби Задания с самопроверкой Проценты и дроби 95
Формула суммы n-первых членов геометрической прогрессии Формула суммы n-первых членов геометрической прогрессии 80
Фигура Квадрат презентация к уроку по математике (младшая группа) Фигура Квадрат презентация к уроку по математике (младшая группа) 57