- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Пятый постулат Евклида. Неевклидова геометрия
Содержание
- 2. ВведениеЕсли две прямые, лежащие в одной плоскости,
- 3. Евклид
- 4. Адриен Мари Лежандр
- 5. Карл Фридрих Гаусс
- 6. Янош Бояи (Больяй)
- 7. Геометрия Лобачевского
- 8. АксиомаЧерез точку, лежащую вне прямой в плоскости,
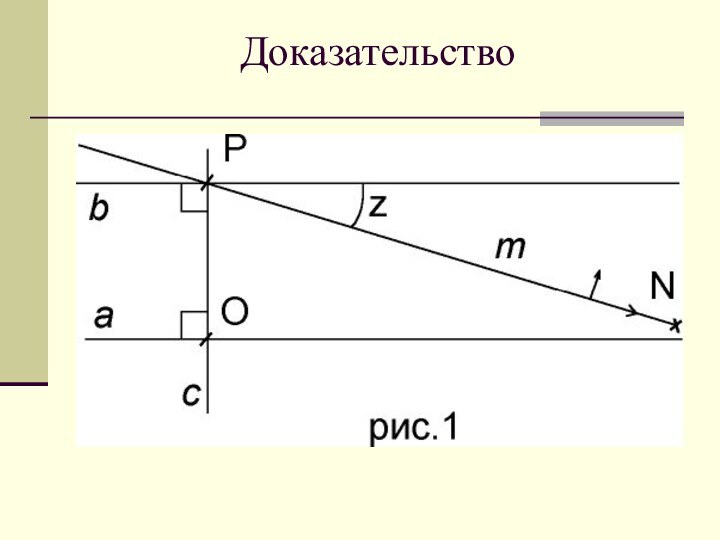
- 9. Доказательство
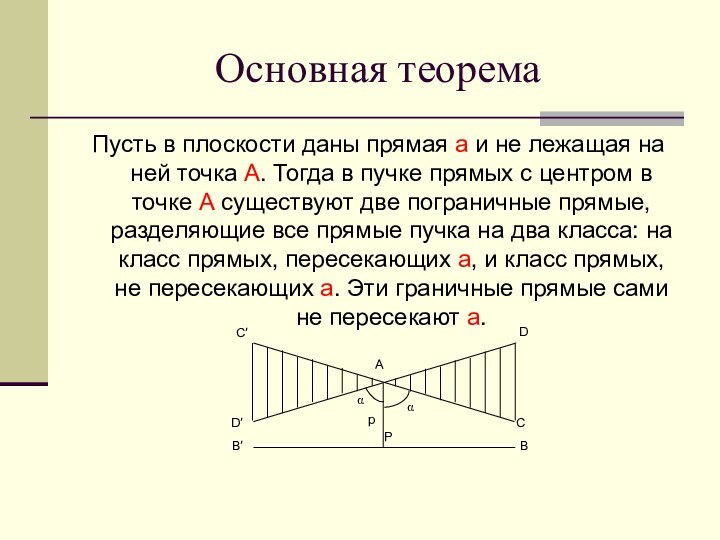
- 10. Основная теоремаПусть в плоскости даны прямая a
- 11. ОпределениеПрямая C'C называется параллельной прямой B'B в
- 12. Сферическая геометрияОпределение 1 Большим кругом называется часть
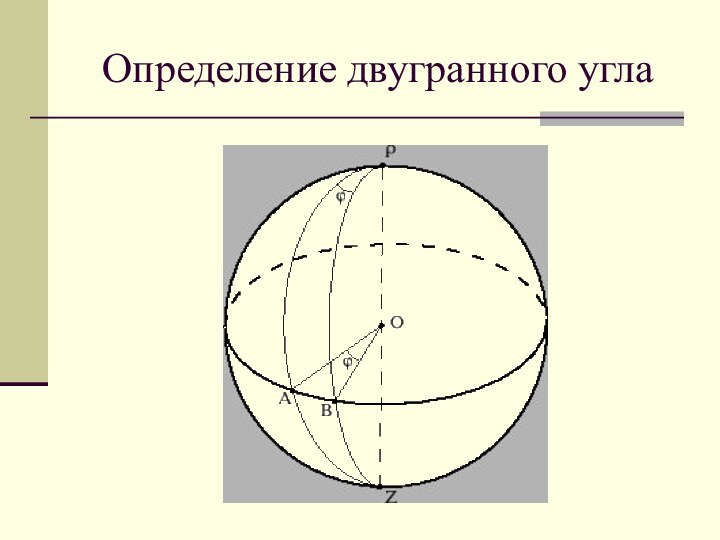
- 13. Определение двугранного угла
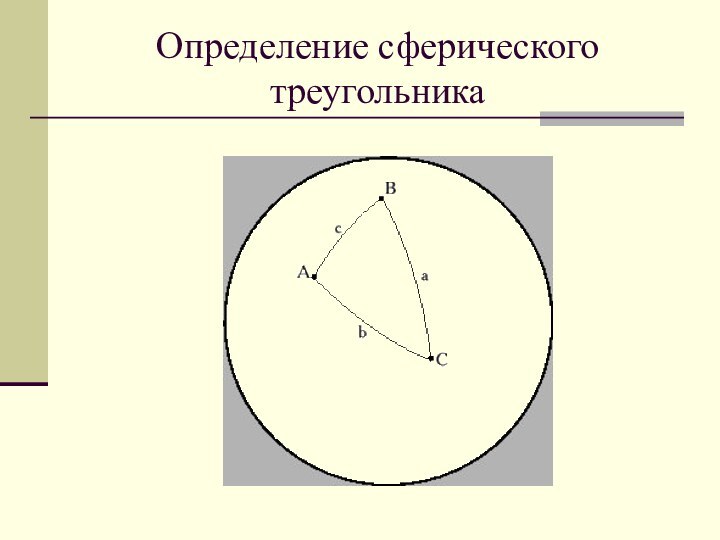
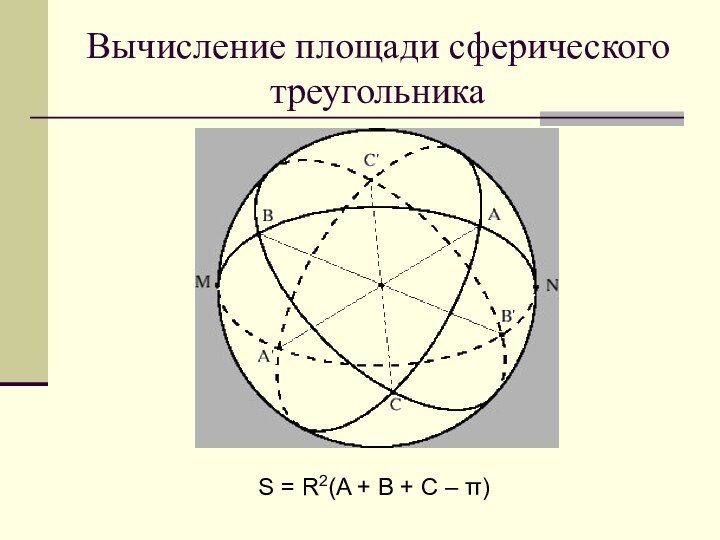
- 14. Определение сферического треугольника
- 15. Вычисление площади сферического треугольника S = R2(A + B + C – π)
- 16. Заключение
- 17. Скачать презентацию
- 18. Похожие презентации
ВведениеЕсли две прямые, лежащие в одной плоскости, пересечены третьей и если сумма внутренних односторонних углов меньше двух прямых углов, то эти прямые пересекутся с той стороны, где это имеет место.