Презентация на тему Угол между прямыми. Угол между прямой и плоскостью

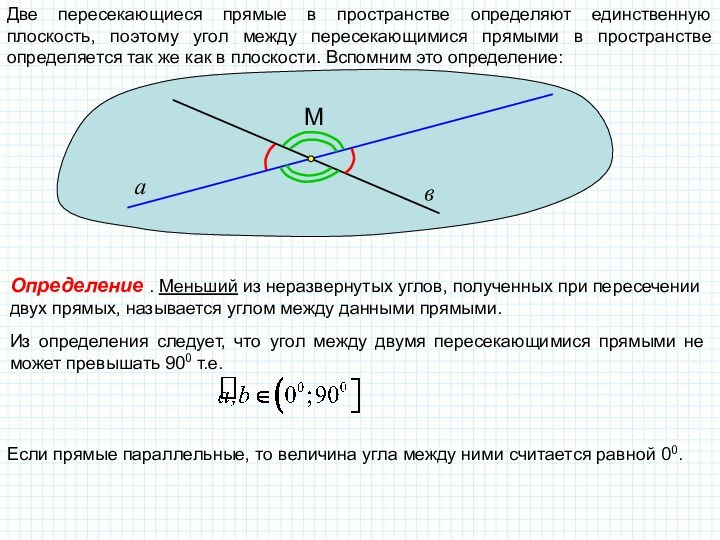
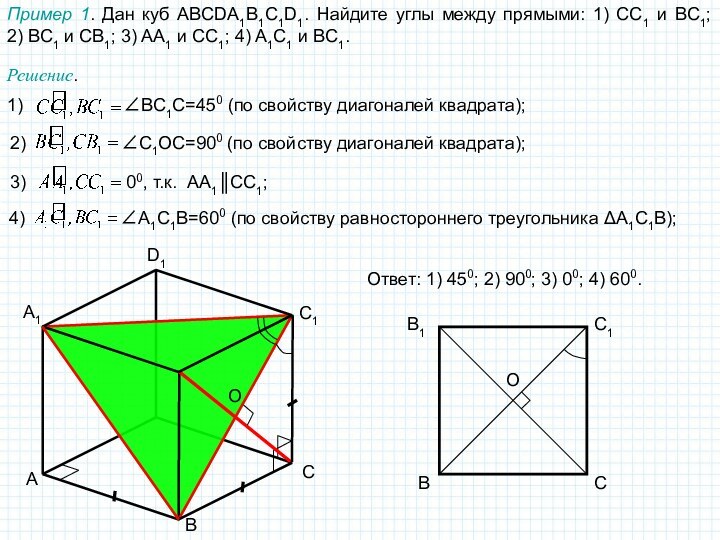
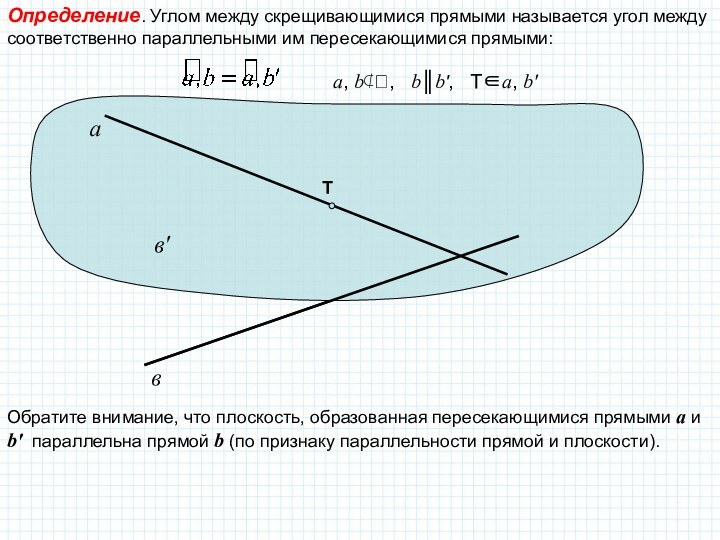
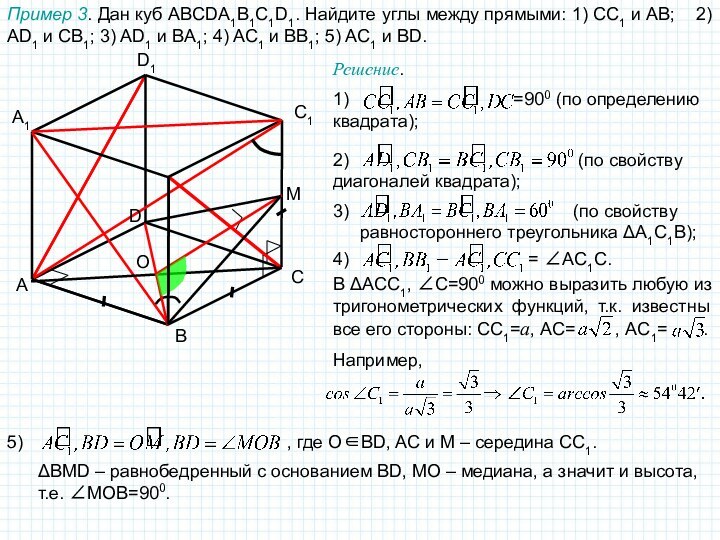
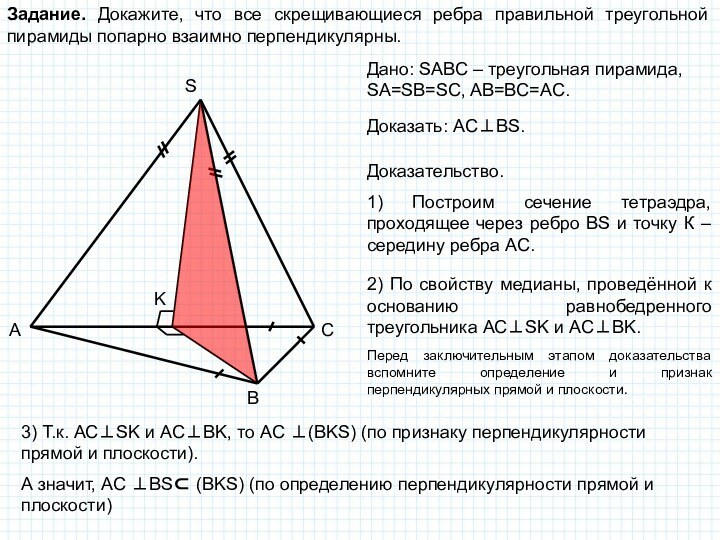
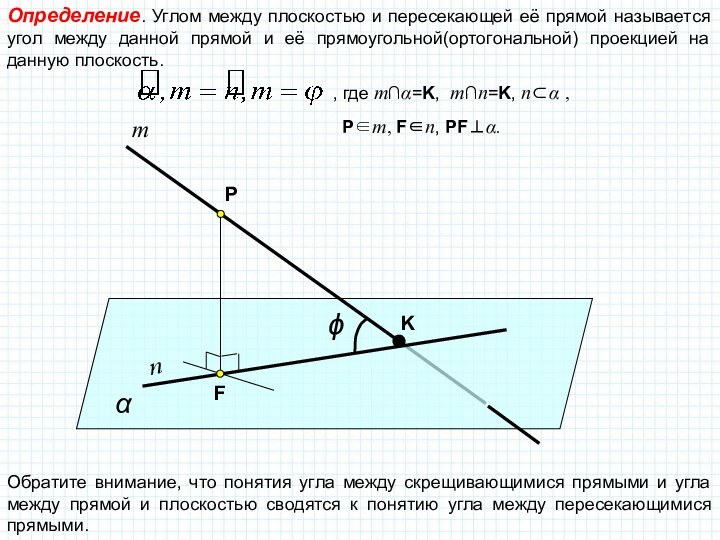
поэтому угол между пересекающимися прямыми в пространстве определяется так

а

в

М

Определение . Меньший из неразвернутых углов, полученных при пересечении двух прямых, называется углом между данными прямыми.

Из определения следует, что угол между двумя пересекающимися прямыми не может превышать 900 т.е.

Если прямые параллельные, то величина угла между ними считается равной 00.

прямыми: 1) CC1 и BC1; 2) BC1 и

B

C

C1

В1

О

О

Ответ: 1) 450; 2) 900; 3) 00; 4) 600.

прямыми обычно рассматривают треугольник, в который входит интересующий нас

Пример 2. Дан прямоугольный параллелепипед ABCDA1B1C1D1, AB=4 см, ВС=3 см, ВВ1=2 см. Найдите углы между прямыми: 1) CC1 и BC1; 2) BC1 и CB1; 3) AA1 и CC1; 3) A1C1 и BC1.

О

соответственно параллельными им пересекающимися прямыми:
а
в
в'
T
a, b⊄, b║b',

Обратите внимание, что плоскость, образованная пересекающимися прямыми a и b′ параллельна прямой b (по признаку параллельности прямой и плоскости).

прямыми: 1) CC1 и АB; 2) AD1 и

O

M

ΔBMD – равнобедренный с основанием BD, МО – медиана, а значит и высота, т.е. ∠MOB=900.

D

пирамиды попарно взаимно перпендикулярны.
A
B
C
S
K
Дано: SABC – треугольная пирамида, SA=SB=SC,

Доказать: AC⊥BS.

Доказательство.
1) Построим сечение тетраэдра, проходящее через ребро BS и точку К – середину ребра АС.

2) По свойству медианы, проведённой к основанию равнобедренного треугольника АС⊥SK и AC⊥BK.

3) Т.к. АС⊥SK и AC⊥BK, то АС ⊥(BKS) (по признаку перпендикулярности прямой и плоскости).
А значит, АС ⊥BS⊂ (BKS) (по определению перпендикулярности прямой и плоскости)

Перед заключительным этапом доказательства вспомните определение и признак перпендикулярных прямой и плоскости.

называется угол между данной прямой и её прямоугольной(ортогональной) проекцией

т

α

n

K

, где m∩α=K, m∩n=K, n⊂α ,
P∈m, F∈n, PF⊥α.

ϕ

P

F

Обратите внимание, что понятия угла между скрещивающимися прямыми и угла между прямой и плоскостью сводятся к понятию угла между пересекающимися прямыми.

: 1) BC1 и (АBC); 2) A1C1 и

B

C1

a