- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Расширение понятия числа
Содержание
- 2. Расширение понятия числаКомплексные числаCOMPLEX
- 3. Принцип преемственности М.В.ЛомоносоваНевозможное должно стать возможнымВсе верное должно остаться верным(эволюционный подход к науке)
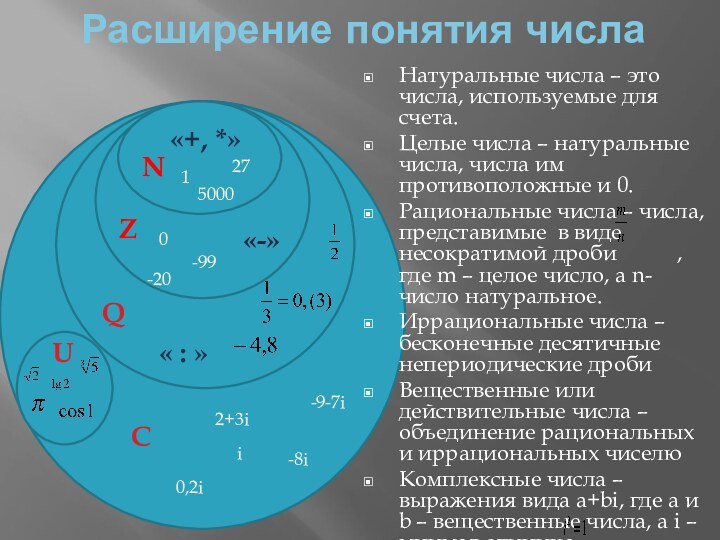
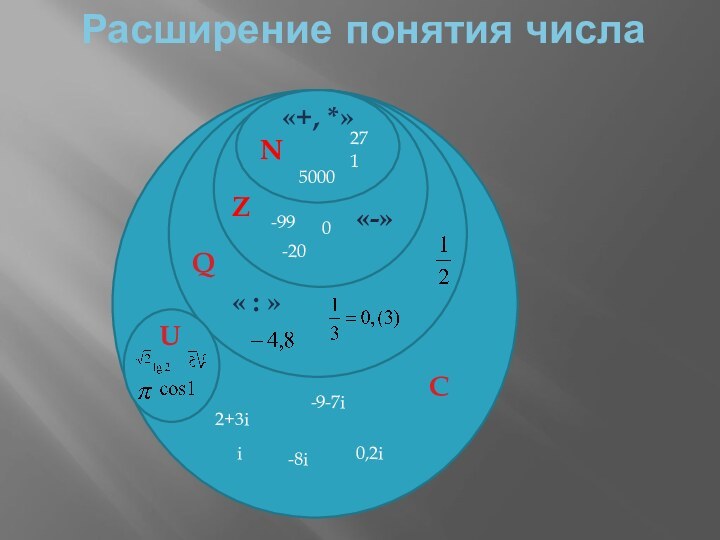
- 4. Расширение понятия числаN1500027«+, *»Z0-20-99«-»Q« : »UСi-8i0,2i2+3i-9-7i
- 5. Мнимая единица.Т.к. любое отрицательное число можно представить
- 6. Задание № 1.Вычислить:
- 7. Комплексные числаМножество, состоящее из выражений вида z=a+bi
- 8. Задание № 2.Даны два комплексных числа
- 9. Задание № 2 (продолжение)Для z=a+bi комплексное числа
- 10. Свойства действий над комплексными числами.Переместительный закон:Сочетательный закон: Распределительный закон:Формулы сокращенного умножения:
- 11. Элементы комплексного числа. z=a+bi
- 12. Равенство комплексных чиселКомплексные числа
- 13. Скачать презентацию
- 14. Похожие презентации
Расширение понятия числаКомплексные числаCOMPLEX











Слайд 3
Принцип преемственности М.В.Ломоносова
Невозможное должно стать возможным
Все верное должно
остаться верным
Слайд 5
Мнимая единица.
Т.к. любое отрицательное число можно представить в
виде произведения -1 и числа противоположного данному, то задачу
вычисления корня из отрицательного числа можно свести к задаче вычисления корня из -1.Например:
Введем число i такое что
Данное число назовем мнимой единицей.
Слайд 7
Комплексные числа
Множество, состоящее из выражений вида z=a+bi ,
где и а, b –
действительные числа, называется множеством комплексных чисел.При этом сложение, вычитание, умножение и деление двух чисел в этом множестве определены соответственно следующим правилами:
(a+bi)+(c+di)=(a+c)+(b+d)i
(a+bi)-(c+di)=(a-c)+(c-d)i
(a+bi)(c+di)=(ac+bd)+(ad+bc)i
Слайд 8
Задание № 2.
Даны два комплексных числа
Найти их сумму, разность и произведение.
Мнемоническое правило:
«действуй как
с многочленами»
Слайд 9
Задание № 2 (продолжение)
Для z=a+bi комплексное числа
называется сопряженным .
Свойство:
Правило деления:
Даны два комплексных числа
Выполнить деление
Слайд 10
Свойства действий над комплексными числами.
Переместительный закон:
Сочетательный закон:
Распределительный
закон:
Формулы сокращенного умножения:
Слайд 11
Элементы комплексного числа.
z=a+bi
a – вещественная
часть числа, Re(z)=ab – мнимая часть числа, Im(z)=b
Пример: 3-8i , 5i , 10
а – вещественное число, bi – чисто мнимое число
Модулем комплексного числа z называют корень из суммы квадратов его вещественной и мнимой части.
Свойство:
Вычислить |z|
3-4i -7i
9 1+2i
Слайд 12
Равенство комплексных чисел
Комплексные числа
равны
Операция сравнения для комплексных чисел
неопределена.Пример: Найдите действительные числа x и y из равенства (3x-y)+(x+y)i=6-2i