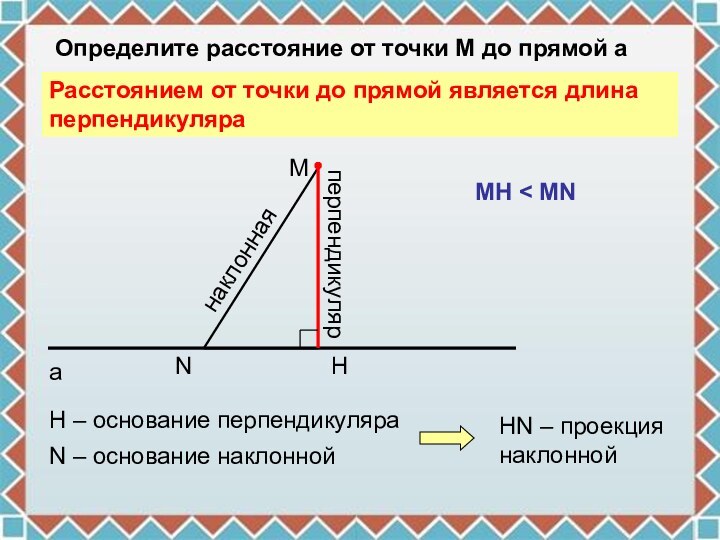
– основание перпендикуляра
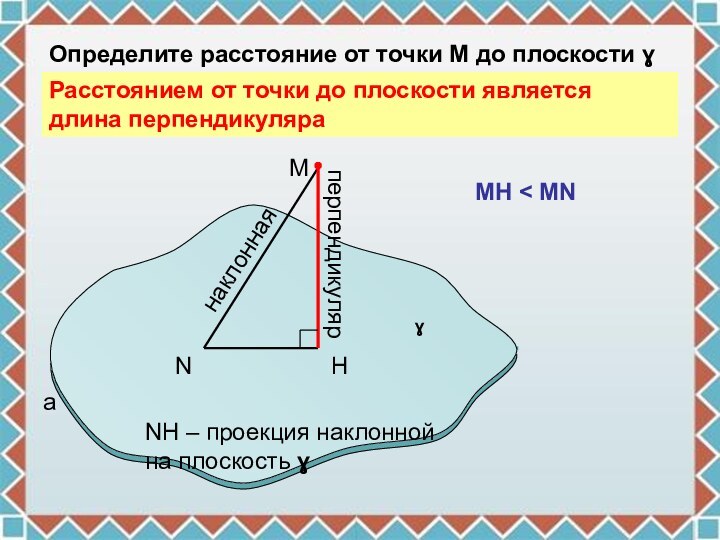
наклонная
N – основание наклонной
HN – проекция наклонной
Расстоянием
от точки до прямой является длина перпендикуляраMH < MN
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть




MH < MN
P
A
B
C
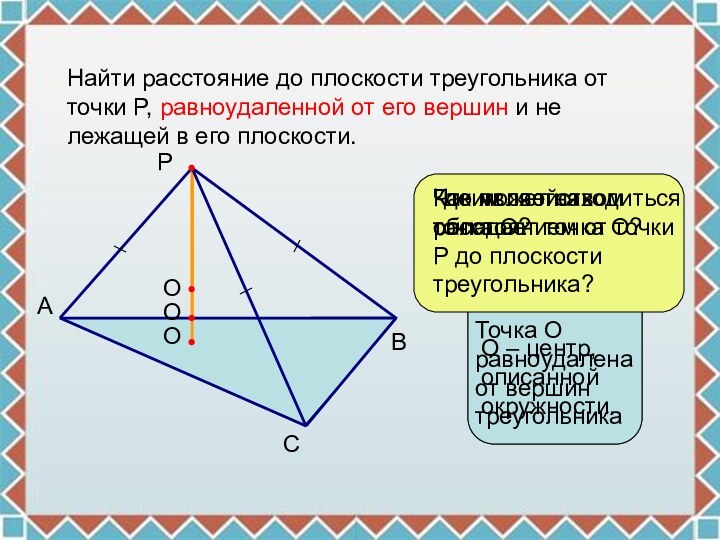
Что является расстоянием от точки Р до плоскости треугольника?
О
О
О
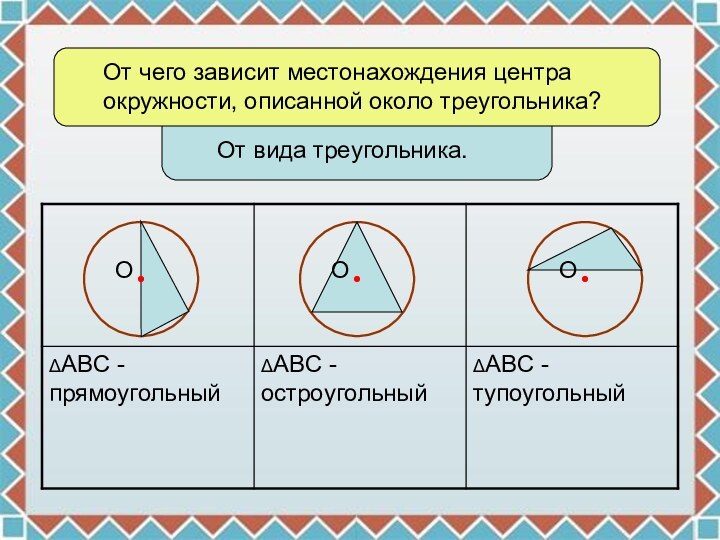
Где может находиться точка О?
Каким свойством обладает точка О?
Точка О равноудалена от вершин треугольника
О – центр, описанной окружности.