Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Графики и функции в основной школе

Содержание

2. Постройте график функции и найдите все значения
3. КомментарийДеятельность учащихся направлена на анализ условия
4. Поиск способа решения1. Что нужно сделать, для
5. КомментарийДеятельность учащихся направлена на поиск способов решения
6. Оформление решения задачиD(у)= (-∞: -
7. Поиск способа решения1. Что представляет собой график
8. Оформление решения задачи yx02-3 а= -4, а=6, а= - 6,25Ответ: а= -4, а=6, а= - 6,25
9. КомментарийДеятельность учащихся направлена на оформление решения
10. Подведение итогов1. Какого типа рассматривалась задача?Ответ :
11. Скачать презентацию
12. Похожие презентации

Постройте график функции и найдите все значения а, при которых прямая у=а имеет с графиком данной функции ровно одну общую точку.1. О чем говорится в задаче? 2. Что известно о функции?3. Что требуется сделать в задаче?у=а

Главная
Математика
Графики и функции в основной школе

Реализация методологических основ обучения решению задач по теме: ,,Графики и

Постройте график функции и найдите все значения а, при которых прямая у=а

КомментарийДеятельность учащихся направлена на анализ условия задачи.Самостоятельную успешность учащихся обеспечивают приёмы:

Поиск способа решения1. Что нужно сделать, для того, чтобы построить график функции?Ответ:

КомментарийДеятельность учащихся направлена на поиск способов решения данной задачиСамостоятельную успешность учащихся обеспечивают

Оформление решения задачиD(у)= (-∞: - 2)ᴗ(-2: 3)ᴗ(3: +∞)Пусть

Поиск способа решения1. Что представляет собой график функции у=а?Ответ: прямая параллельная оси

Оформление решения задачи yx02-3 а= -4, а=6, а= - 6,25Ответ: а= -4, а=6, а= - 6,25

КомментарийДеятельность учащихся направлена на оформление решения задачи.Самостоятельную успешность учащихся обеспечивают приёмы:использование

Подведение итогов1. Какого типа рассматривалась задача?Ответ : на построение графика функции, на

КомментарийДеятельность учащихся направлена на исследования задачи.Самостоятельную успешность учащихся обеспечивают приёмы:специальная серия

Слайды презентации

Слайд 2 Постройте график функции
и найдите все значения а,

Постройте график функции и найдите все значения а, при которых прямая

при которых прямая у=а имеет с графиком данной функции

ровно одну общую точку.

1. О чем говорится в задаче?

2. Что известно о функции?

3. Что требуется сделать в задаче?

у=а - имеет с графиком одну общую точку

4. Что еще требуется найти?

1) Построить график

2) а - ?

Анализ условия задачи

Слайд 3 Комментарий
Деятельность учащихся направлена на
анализ условия задачи.
Самостоятельную

успешность учащихся обеспечивают приёмы:
специальная серия вопросов (о чем

идет речь, что известно о функции и т.д.;
подчёркивание в тексте задачи ответов на вопросы диалога, что обеспечивает понимание;
краткая запись условия.

Слайд 4 Поиск способа решения
1. Что нужно сделать, для того,

Поиск способа решения1. Что нужно сделать, для того, чтобы построить график

чтобы построить график функции?
Ответ: а) найти область определения данной

функции;

2. Как упрощают выражения записанные дробью?

Ответ: сокращением дробей.

3. Что для этого нужно сделать?

Ответ: разложить числитель на множители

4. Можно ли числитель разложить на множители? Как?

Ответ: да, решить биквадратное уравнение.

б) упростить выражение.

5. Каковы корни данного биквадратного уравнения?

Ответ: 9 и 4.

6. Какого вида оказалась функция после сокращения?

Ответ: квадратичная

7. Что является графиком квадратичной функции?

Ответ: парабола

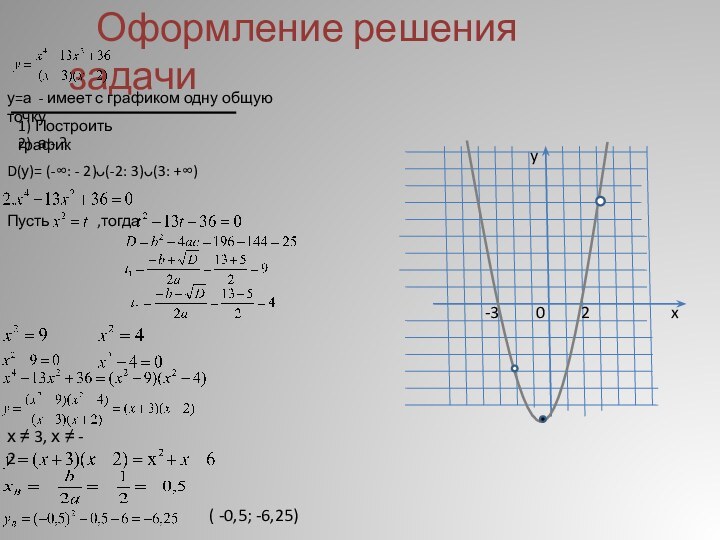
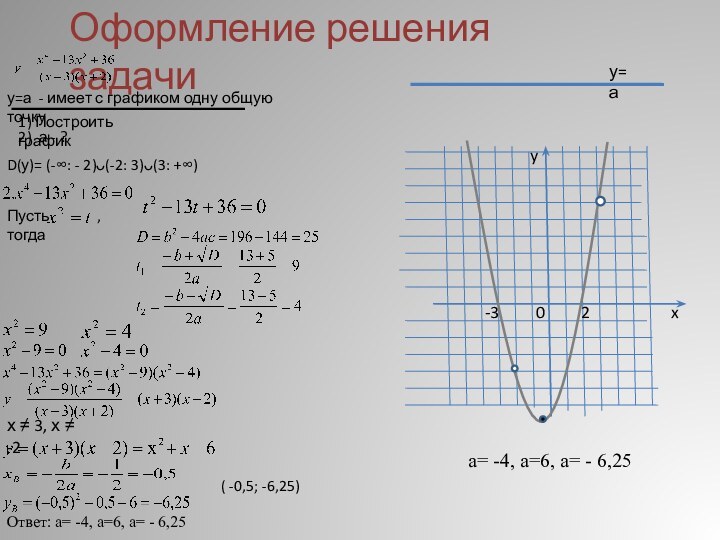
План решения:

1. Найти область определения.

2. Упростить график функции на области определения.

3. Построить график функции.

Слайд 5 Комментарий
Деятельность учащихся направлена на
поиск способов решения

КомментарийДеятельность учащихся направлена на поиск способов решения данной задачиСамостоятельную успешность учащихся

данной задачи
Самостоятельную успешность учащихся обеспечивают приёмы:
специальная серия вопросов;

составление плана решения;

- анимация текста;

Слайд 6 Оформление решения задачи
D(у)= (-∞: - 2)ᴗ(-2:

3)ᴗ(3: +∞)
Пусть ,тогда

х ≠ 3, х ≠ - 2

-3

( -0,5; -6,25)

Слайд 7 Поиск способа решения
1. Что представляет собой график функции

Поиск способа решения1. Что представляет собой график функции у=а?Ответ: прямая параллельная

у=а?
Ответ: прямая параллельная оси ОХ.
2. Что требуется выяснить?
Ответ: значения

а, при которых прямая с графиком имеет одну точку.

3. Каким способом можем это выяснить?

Ответ: двигаем прямую вдоль оси ОУ по всей параболе.

Слайд 8 Оформление решения задачи

y
x
0
2
-3

а= -4, а=6, а=

- 6,25

Ответ: а= -4, а=6, а= - 6,25

Слайд 9 Комментарий
Деятельность учащихся направлена на
оформление решения задачи.
Самостоятельную

успешность учащихся обеспечивают приёмы:
использование предыдущих знаний по решению биквадратных

уравнений;
поэтапная запись решения уравнения;
составленный план решения задачи;
график функции со всеми данными и искомыми элементами;
поэтапная реализация шагов плана за счет анимации.