- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Различные доказательства теоремы Пифагора
Содержание
- 2. Теорема Пифагора
- 3. Структура задачиДаноЧто нужно доказатьДоказательство
- 4. CAB–прямоугольный треугольник ABcДано:
- 5. Доказать: SBAED=SFGAC+SHCBIПостроим нужные нам квадратына сторонах треугольника:
- 6. Доказательство
- 7. Опустим из вершины С прямого угла перпендикуляр
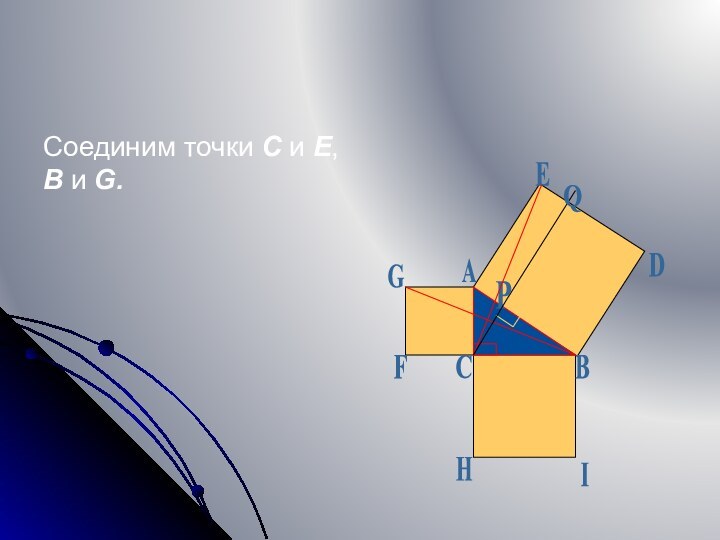
- 8. Соединим точки C и E, B и G.BCDEFGHIQPA
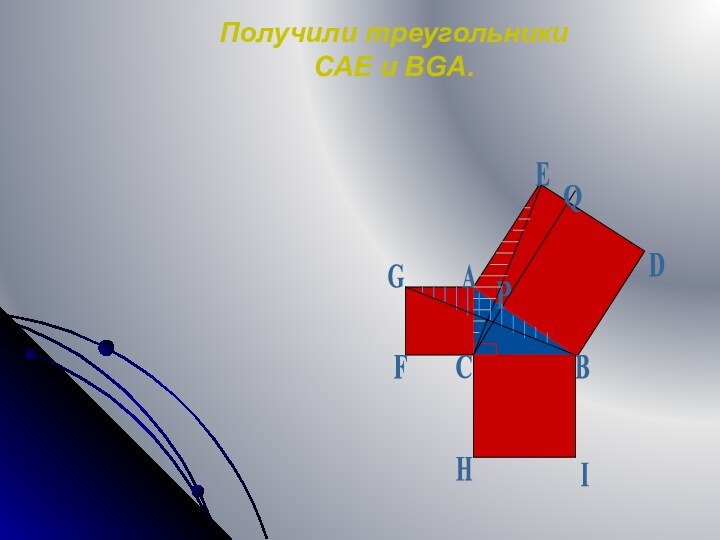
- 9. Получили треугольники
- 10. Очевидно, что углы CAE=GAB(=A+90°); Отсюда следует, что
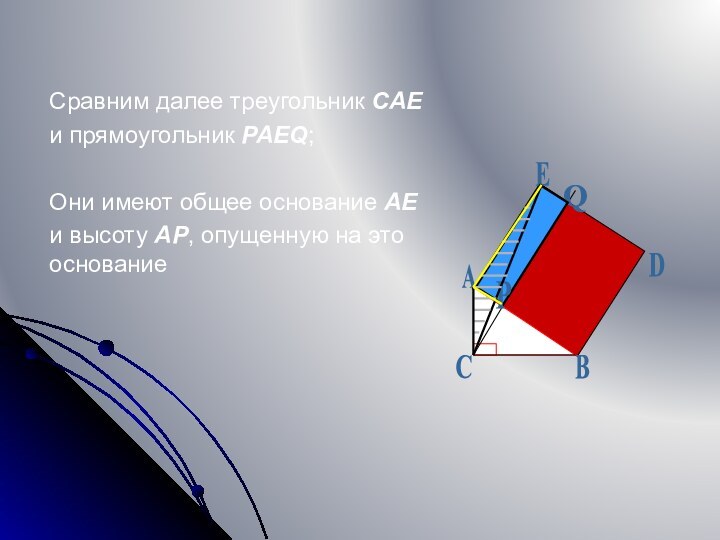
- 11. Сравним далее треугольник CAE и прямоугольник PAEQ;Они
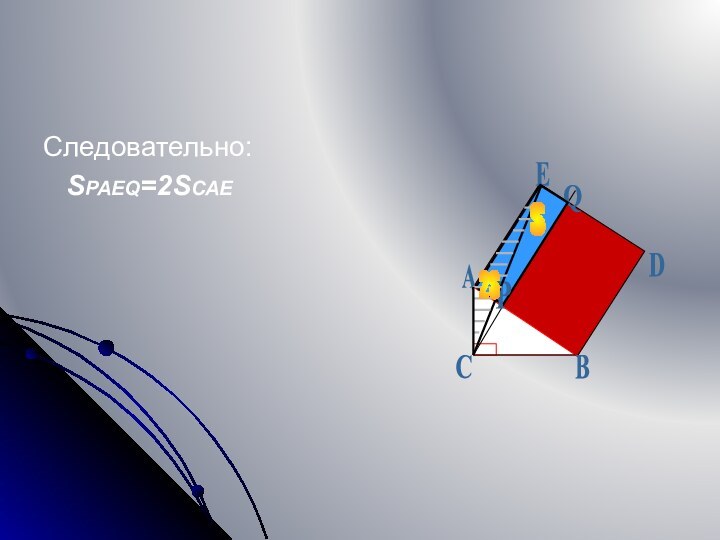
- 12. Следовательно: SPAEQ=2SCAE ABCDEQPS2S
- 13. Точно так же квадрат FGAC и треугольник
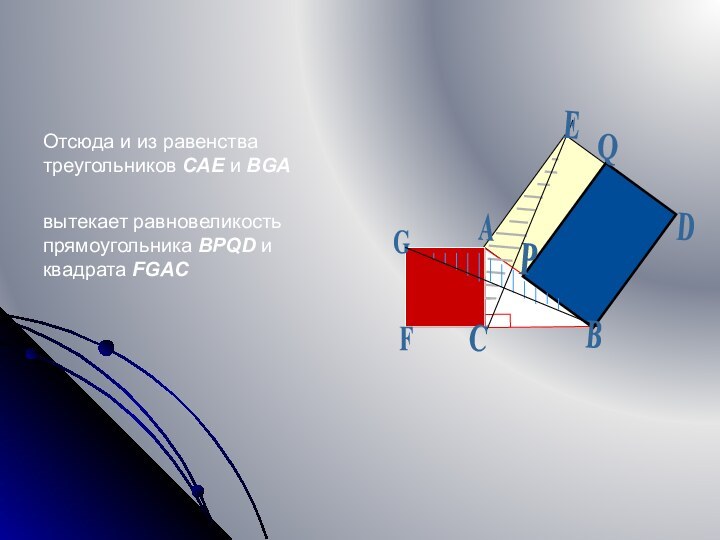
- 14. Отсюда и из равенства треугольников CAE и BGA вытекает равновеликость прямоугольника BPQD и квадрата FGACDQPGFACEB
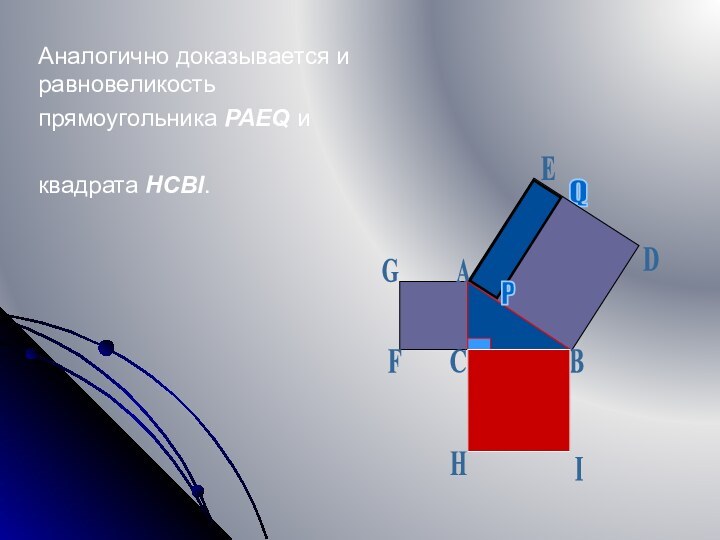
- 15. Аналогично доказывается и равновеликость прямоугольника PAEQ и квадрата HCBI.QP
- 16. Скачать презентацию
- 17. Похожие презентации
Теорема Пифагора







Слайд 5
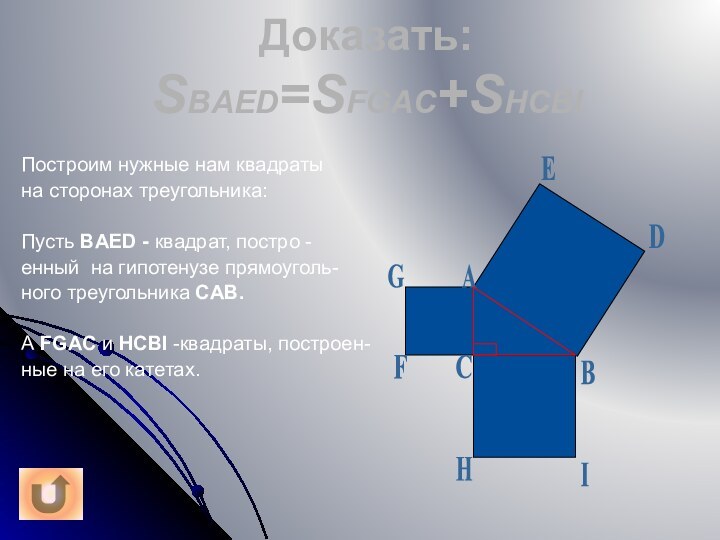
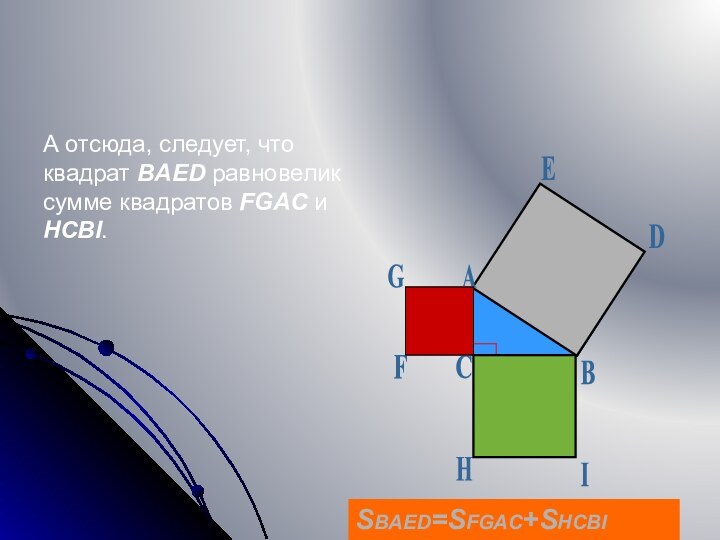
Доказать: SBAED=SFGAC+SHCBI
Построим нужные нам квадраты
на сторонах треугольника:
Пусть
BAED - квадрат, постро -
енный на гипотенузе прямоуголь-
ного треугольника
CAB.А FGAC и HCBI -квадраты, построен-
ные на его катетах.
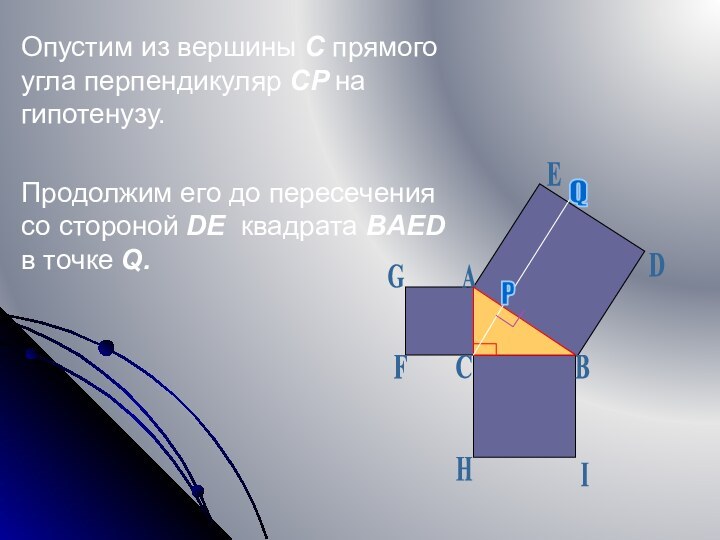
Слайд 7 Опустим из вершины С прямого угла перпендикуляр CP
на гипотенузу.
Продолжим его до пересечения со стороной DE
квадрата BAED в точке Q.A
B
C
D
E
F
G
H
I
Q
P
Слайд 10
Очевидно, что углы CAE=GAB(=A+90°);
Отсюда следует, что треугольники
CAE и BGA(заштрихованные на рисунке) равны между собой (по
двум сторонам и углу, заключённому между ними).D
Q
P
B
E
F
G
C
A
Слайд 11
Сравним далее треугольник CAE
и прямоугольник PAEQ;
Они имеют
общее основание AE
и высоту AP, опущенную на это
основаниеA
B
C
D
E
Q
P
Слайд 13
Точно так же квадрат FGAC
и треугольник
BGA
имеют общее основание GA
высоту AC
Значит
SFGAC=2SBGA A
C
F
G
B
S
2S