Презентация на тему Разложение многочлена на множители с помощью комбинации различных приемов

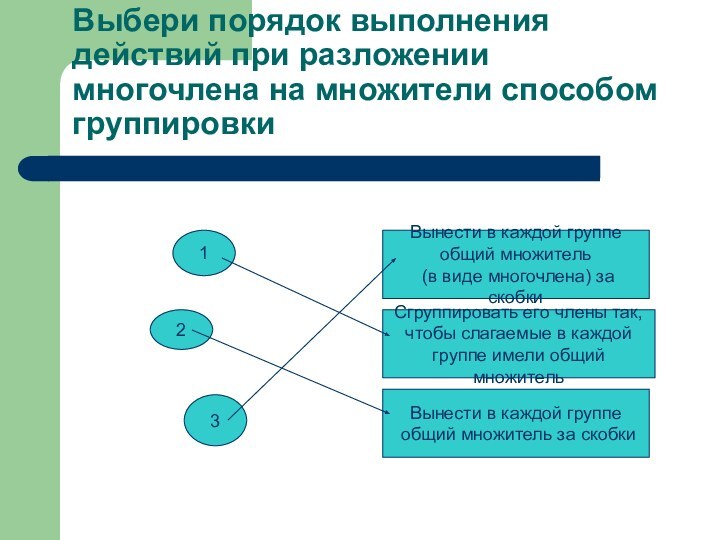
множители способом группировки
1
2
3
Вынести в каждой группе
общий множитель
(в

виде многочлена) за скобки

Сгруппировать его члены так,
чтобы слагаемые в каждой
группе имели общий множитель

Вынести в каждой группе
общий множитель за скобки

+ b2- 2аb = ( а -

b )2;
б) т2 + 2тп - п2 = ( т - п )2;
в ) 2рк - р2- к2 = ( р - к )2;
г) 2са + с2 + а2 = ( с + а )2.

+

+

9
2bх - Зау – 6bу +ах

а 4 - Ь2
27с3

+ а6

с 2 + ас – 5а – 5с

в(а + 5) -с(а + 5)

9x2 + y4

Вынесение общего
множителя
за скобки

Не раскладывается
на множители

Способ
группировки

Формулы сокращенного
умножения

обшего
множителя за скобки
4а4 + 25b2
Формула

сокращенного
умножения

49т 4 - 25п

Нне раскладывается
на множители

3a2 + 3ab - 7a – 7b

Способ группировки

x2 + 6x +. 9

2у(х-5) + x (х-5)

15 а3b +3a2b3

выносится некоторый одночлен, входящий в качестве множителя во все

слагаемые.
Таким общим множителем может быть не только одночлен, но и многочлен.

но после заключения нескольких членов в скобки (на основе

переместительного и сочетательного законов сложения) удается выделить общий множитель, являющийся многочленом.

трех (или более) слагаемых, которая обращает выражение, входящее в

одну из формул сокращенного умножения, заменяется произведением многочленов.

b)
3.  (За-4b) (За+ 4b )
4.  7аb (а-2b +1 )
5. 

(m-q )(m+ n –1 )
6.  (2а- b)2
7. (2а + с) (За + 2b )
8. (5а + 7b )2

1. (4а + b)2 .
2. (3 +n ) (m-n )
3. 5 ( а –5b )
4. (а- q)(а-3b+1)
5. (3а-5b)2
6. (2a + 3b)(а + 2с)
7. (12а-5b) (12а+ 5b)
8. 9аb ( а2-2b-1 )

(если он есть).
2.     Попробовать разложить многочлен на множители по

формулам сокращенного умножения.
3.     Попытаться применить способ группировки (если предыдущие способы не привели к цели).

- 15x + 56 = 0

Решение :

x2 - 7x - 8x +56 = 0
( x2 - 7x) - ( 8x - 56 ) = 0
x (x - 7 ) - 8 (x - 7 ) = 0
( x - 7 ) ( x - 8 ) = 0
x - 7 = 0 или x - 8 = 0
x = 7 или х = 8

- n2   Задание № 2 ( 3n - 4

)2 - n2  

Решение :

(3n- 4)2 -n2 = (3n - 4 - n )( 3n - 4 + n ) =
( 2n - 4) (4n - 4) = 8 (n - 2 ) (n - 1 )

+ Зn2 + 2n = n (n2 + Зn

+ 2) =
n (n2 + 2n + n + 2) =
n ((n2 + 2n) + (n + 2)) =
n (n (n + 2) + n + 2) = n (n + 1) (n + 2). 
Комбинировали три приема:
-   вынесение общего множителя за скобки;
-   предварительное преобразование;
-   группировку.
Отмечаем, что для решения этого примера мы использовали еще один прием разложения на множители - предварительное преобразование.