- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Учебно-исследовательская работа Многогранники
Содержание
- 2. Введение При исследовании многогранников перед
- 3. МногогранникиС древнейших времен наши представления о красоте
- 4. Многогранник Это пространственное тело с плоскими
- 5. Простейшими примерами многогранников служат пирамиды и призмыУ
- 6. Антипризма (призмоид) Основания одинаковые, но расположены различно:
- 7. Для любого выпуклого многогранника справедливо
- 8. Теорема Эйлера
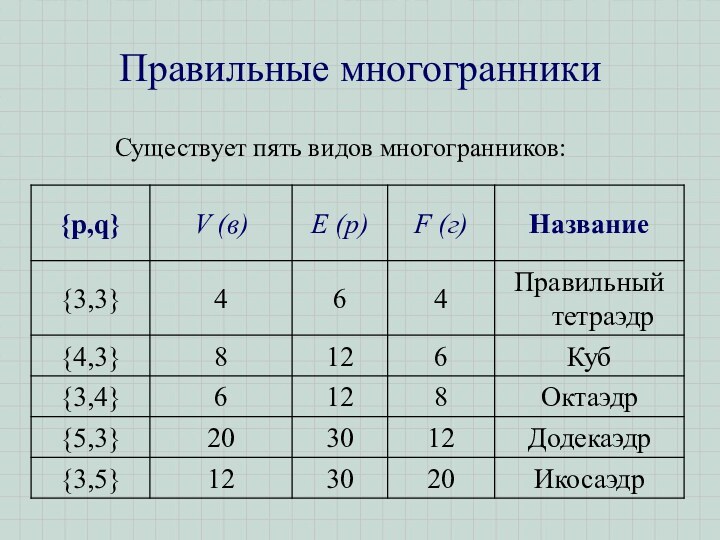
- 9. Правильные многогранники Существует пять видов многогранников:
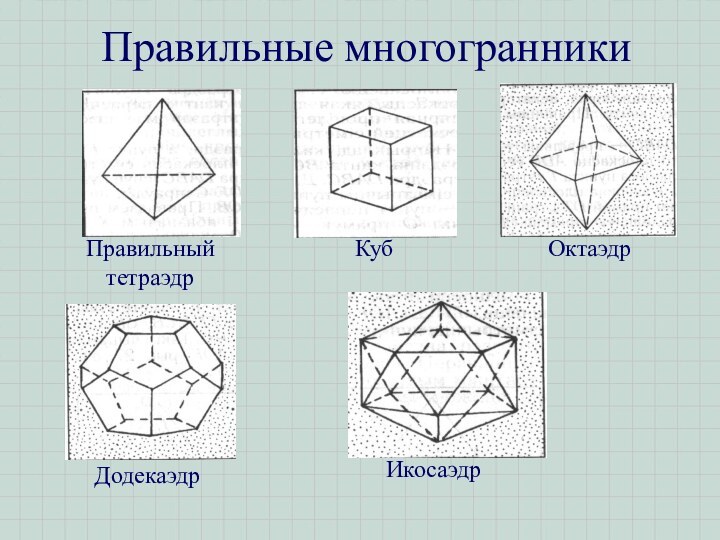
- 10. Правильные многогранники
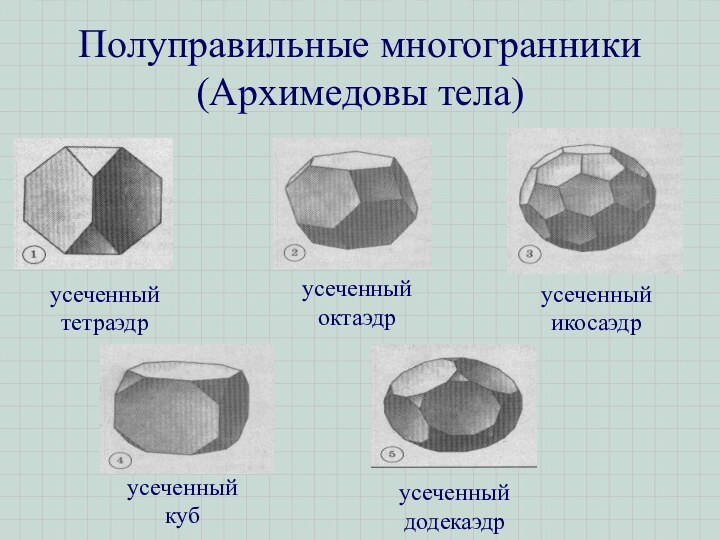
- 11. Полуправильные многогранники (Архимедовы тела)
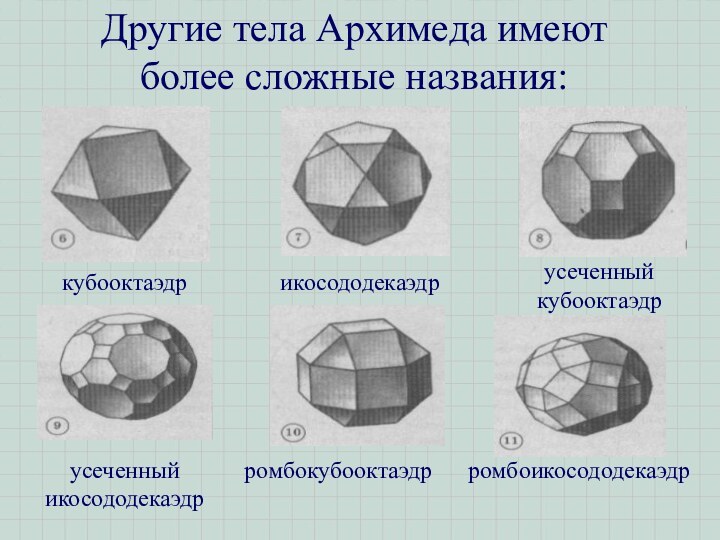
- 12. Другие тела Архимеда имеют более сложные названия:
- 13. Вращающие кольца тетраэдров Дж. М. Андреас и Р.
- 14. Модель кольца из 6 тетраэдровПри n=6 фигура ещё жесткая, поэтому полностью не выворачивается
- 15. Модель кольца из 8 тетраэдров
- 17. Заключение: Проводя исследования по данной теме, мы
- 18. Скачать презентацию
- 19. Похожие презентации
Введение При исследовании многогранников перед собой мы поставили следующие задачи:Изучить разновидности многогранников.Научиться строить некоторые модели многогранников.Исследовать вращающие кольца тетраэдров.












Слайд 2
Введение
При исследовании многогранников перед собой мы
поставили следующие задачи:
вращающие кольца тетраэдров.
Слайд 3
Многогранники
С древнейших времен наши представления о красоте связаны
с симметрией. Наверное, этим объясняется интерес человека к многогранникам
– удивительным символам симметрии, привлекавшим внимание выдающихся мыслителей.
Слайд 4
Многогранник
Это пространственное тело с плоскими гранями
и прямолинейными ребрами, устроенное так, чтобы всякое ребро соединяет
две вершины и служит общей стороной двух граней
Слайд 5
Простейшими примерами многогранников служат пирамиды и призмы
У пятиугольной
призмы:
10 вершин
15 ребер
7 граней
У пятиугольной пирамиды:
6 вершин
10 ребер
6 граней
Слайд 6
Антипризма (призмоид)
Основания одинаковые, но расположены различно: вершины каждого
из оснований лежат над сторонами другого, так что боковые
ребра идут зигзагомУ пятиугольной антипризмы:
10 вершин
20 ребер
12 граней
Слайд 7
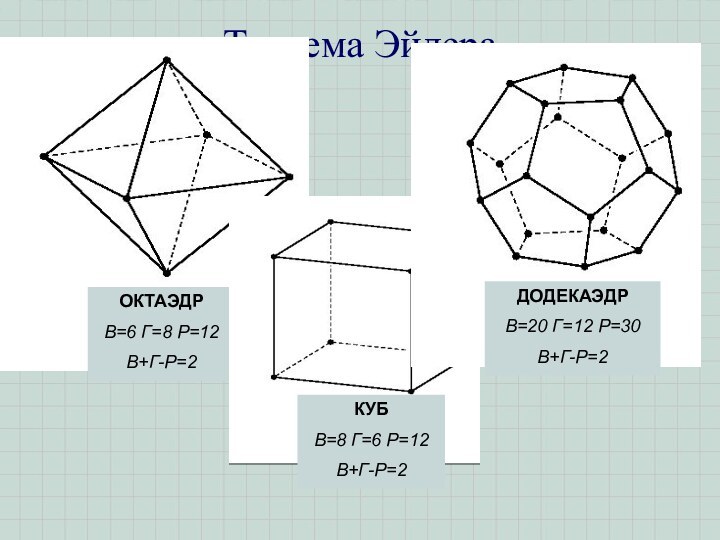
Для любого выпуклого многогранника справедливо соотношение
Г+В-Р=2
Г- число граней,
В- число вершин,Р- число ребер данного многогранника
Теорема Эйлера
Слайд 13
Вращающие кольца тетраэдров
Дж. М. Андреас и Р. М.
Сталкер независимо друг от друга открыли семейство изгибаемых конечных
многогранников с 2n вершинами, 6n ребрами и 4n треугольными гранями. Гранями служат грани n тетраэдров, соединенных между собой в циклическом порядке по определенным парам противоположных ребер каждого, так что получается фигура наподобие кольца.
Слайд 14
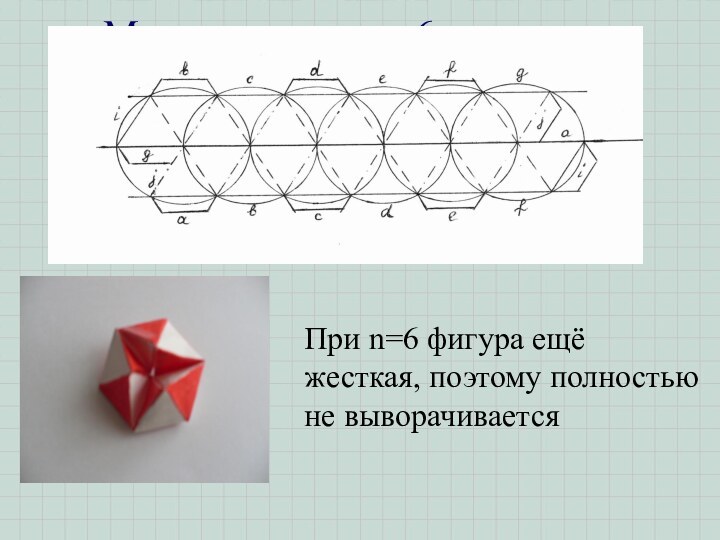
Модель кольца из 6 тетраэдров
При n=6 фигура ещё
жесткая, поэтому полностью не выворачивается
Слайд 17
Заключение:
Проводя исследования по данной теме, мы изучили исторические
данные по многогранникам;
При построении разверток многогранников мы научились работать
с чертежными инструментами;Создавая модели призмы, антипризмы, пирамиды, а также вращающих колец из тетраэдров мы расширили свое пространственное воображение.
В дальнейшей работе мы хотим научиться строить модели более сложных по виду многогранников.





























