Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Размеры объектов, трансформация октаэдра

Содержание

2. Часто необходимо решать, задачи, связанные с размерами
3. При решении таких задач фигуры стараются расположить
4. Плоская фигура, например, имеет на одной из
5. Определение истинных размеров параллелограмма с помощью поворота в плоскости проекций
6. Если вращать параллелограмм вокруг стороны АВ, то
7. Поскольку плоскость такой окружности перпендикулярна первой плоскости
8. Следовательно, при вращении параллелограмма точка С' будет
9. Обозначим это положение точки С через С*.
10. Полученный в результате вращения параллелограмм ABC*D* имеет
11. По этой причине для построения изображения «вращения»
12. Построение проекций октаэдра с помощью двух трансформаций
13. Плоскость проекции, введенная дополнительно, должна быть перпендикулярна
14. Пусть мы хотим теперь исключить из рассмотрения
15. расстояние от нее до оси х13 равно
16. На рисунке изображены две проекции правильного тетраэдра
17. Изображение точки на поверхности конуса вращения
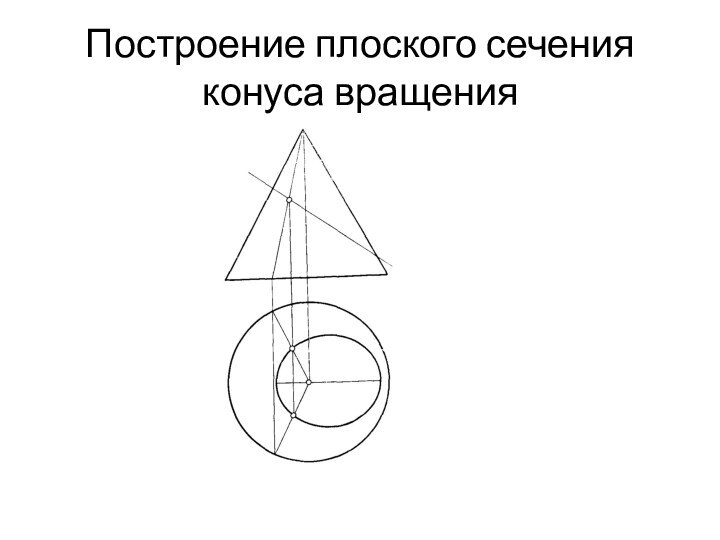
18. Построение плоского сечения конуса вращения
19. Построить точку на некоторой поверхности, например, на
20. Скачать презентацию
21. Похожие презентации

Часто необходимо решать, задачи, связанные с размерами объектов, например, определение размеров некоторой фигуры по ее проекциям или наоборот, построение проекций некоторой фигуры, если известны ее размеры.

Главная
Математика
Размеры объектов, трансформация октаэдра

Л.6. РАЗМЕРЫ ОБЪЕКТОВ, ТРАНСФОРМАЦИЯ ОКТАЭДРА

Часто необходимо решать, задачи, связанные с размерами объектов, например, определение размеров некоторой

При решении таких задач фигуры стараются расположить относительно плоскостей проекций таким образом,

Плоская фигура, например, имеет на одной из проекций истинные размеры, если расположена

Определение истинных размеров параллелограмма с помощью поворота в плоскости проекций

Если вращать параллелограмм вокруг стороны АВ, то каждая его точка — и

Поскольку плоскость такой окружности перпендикулярна первой плоскости проекций, и оси вращения, то

Следовательно, при вращении параллелограмма точка С' будет перемещаться вдоль некоторой прямой, перпендикулярной

Обозначим это положение точки С через С*. Расстояние от точки С* до

Полученный в результате вращения параллелограмм ABC*D* имеет истин ные размеры параллелограмма ABCD.Заметим,

По этой причине для построения изображения «вращения» плоской фигуры достаточно выполнить его

Построение проекций октаэдра с помощью двух трансформаций

Плоскость проекции, введенная дополнительно, должна быть перпендикулярна од ой из «старых» плоскостей.

Пусть мы хотим теперь исключить из рассмотрения плоскость К2 и изобразить точку

расстояние от нее до оси х13 равно расстоянию от точки P

На рисунке изображены две проекции правильного тетраэдра и полученные из них с

Изображение точки на поверхности конуса вращения

Построение плоского сечения конуса вращения

Построить точку на некоторой поверхности, например, на поверхности конуса вращения, можно с

На рисунке в качестве секущей плоскости для простоты выбрана вторая плоскость проекций;

Слайды презентации

Слайд 2 Часто необходимо решать, задачи, связанные с размерами объектов,

Часто необходимо решать, задачи, связанные с размерами объектов, например, определение размеров

например, определение размеров некоторой фигуры по ее проекциям или

наоборот, построение проекций некоторой фигуры, если известны ее размеры.

Слайд 3 При решении таких задач фигуры стараются расположить относительно

При решении таких задач фигуры стараются расположить относительно плоскостей проекций таким

плоскостей проекций таким образом, чтобы соотношения, связанные с размерами,

можно было установить непосредственно.
.

Слайд 4 Плоская фигура, например, имеет на одной из проекций

Плоская фигура, например, имеет на одной из проекций истинные размеры, если

истинные размеры, если расположена в соответствующей плоскости проекций или

параллельна ей.
В качестве примера рассмотрим параллелограмм ABCD, сторона AB которого лежит в первой плоскости проекций, а сторона AD — во второй

Слайд 5 Определение истинных размеров параллелограмма с помощью поворота в

плоскости проекций

Слайд 6 Если вращать параллелограмм вокруг стороны АВ, то каждая

Если вращать параллелограмм вокруг стороны АВ, то каждая его точка —

его точка — и в том числе, например, вершина

С — будет двигаться по некоторой окружности, центр которой лежит на стороне AB.

Слайд 7 Поскольку плоскость такой окружности перпендикулярна первой плоскости проекций,

Поскольку плоскость такой окружности перпендикулярна первой плоскости проекций, и оси вращения,

и оси вращения, то ее проекцией на первую плоскость

будет некоторый отрезок, перпендикулярный отрезку AB.

Слайд 8 Следовательно, при вращении параллелограмма точка С' будет перемещаться

Следовательно, при вращении параллелограмма точка С' будет перемещаться вдоль некоторой прямой,

вдоль некоторой прямой, перпендикулярной отрезку AB, до тех пор,

пока точка С не достигнет первой плоскости проекций.

Слайд 9 Обозначим это положение точки С через С*. Расстояние

Обозначим это положение точки С через С*. Расстояние от точки С*

от точки С* до оси вращения равно гипотенузе прямоугольного

треугольника, один катет которого равен расстоянию от точки С' до оси вращения, а другой — расстоянию от точки С до первой плоскости проекций.

Слайд 10 Полученный в результате вращения параллелограмм ABCD имеет истин

Полученный в результате вращения параллелограмм ABC*D* имеет истин ные размеры параллелограмма

ные размеры параллелограмма ABCD.
Заметим, что проекция плоской фигуры и

ее изображение в той же плоскости, полученное в результате вращения, могут быть переведены друг в друга с помощью ортогональ ного аффинного преобразования.

Слайд 11 По этой причине для построения изображения «вращения» плоской

По этой причине для построения изображения «вращения» плоской фигуры достаточно выполнить

фигуры достаточно выполнить его для одной из точек фигуры,

тогда все изображение нетрудно построить, основываясь на свойствах аффинного преобразования

Слайд 12 Построение проекций октаэдра с помощью двух трансформаций

Слайд 13 Плоскость проекции, введенная дополнительно, должна быть перпендикулярна од

Плоскость проекции, введенная дополнительно, должна быть перпендикулярна од ой из «старых»

ой из «старых» плоскостей. Если, например, к плоскостям К1

и К2 добавляется плоскость К3, перпендикулярная к К1, то точка Р'‘ является проекцией некоторой точки P на плоскость К3, находится на таком же расстоянии от плоскости К1, как и точка P".

Слайд 14 Пусть мы хотим теперь исключить из рассмотрения плоскость

Пусть мы хотим теперь исключить из рассмотрения плоскость К2 и изобразить

К2 и изобразить точку P в проекциях на плоскости

и К1 и К3, повернув для этого плоскость К3 вокруг линии ее пересечения с плоскостью К1, (вокруг оси х13) до совмещения с K1. Если ось х13задана согласно замечанию, сделанному выше, построить точку P'" не представляет труда:

Слайд 15 расстояние от нее до оси х13 равно расстоянию

от точки P" до оси х12. Переход к новой

системе плоскостей проекций принято называть трансформацией
Трансформацию целесообразно применять и в тех случаях, когда положение фигуры относительно плоскостей проекций таково, что не дает достататочно наглядного представления о фигуре.

Слайд 16 На рисунке изображены две проекции правильного тетраэдра и

На рисунке изображены две проекции правильного тетраэдра и полученные из них

полученные из них с помощью трансформаций третья и четвертая

проекции. Первые две проекции  квадраты с проведенными в них диагоналями. Основываясь на них, до-—трудно представить себе октаэдр. Значительно более наглядное представление об октаэдре дает четвертая проекция.

Слайд 17 Изображение точки на поверхности конуса вращения

Слайд 18 Построение плоского сечения конуса вращения

Слайд 19 Построить точку на некоторой поверхности, например, на поверхности

Построить точку на некоторой поверхности, например, на поверхности конуса вращения, можно

конуса вращения, можно с помощью линий, лежащих на этой

поверхности Для конуса вращения простейшими из таких линии являются его образующие. Линию пересечения конуса вращения с некоторой плоскостью можно построить, отметив точки пересечения произвольного числа образующих с этой плоскостью.