Слайд 2
Эпиграф урока:
.
.
«Число, место и комбинация – три взаимно перекрещивающиеся, но
отличные сферы мышления, к которым можно отнести все математические идеи».
Дж. Сильвестр
Что такое комбинаторика?
Комбинаторика – это раздел математики, в
котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.
Выбором объектов и расположением их в том или ином порядке приходится заниматься чуть ли не во всех областях человеческой деятельности, например конструктору, разрабатывающему новую модель механизма, ученому-агроному, планирующему распределение с/х культур на нескольких полях, химику, изучающему строение органических молекул, имеющих данный атомный состав.
истории комбинаторики
С комбинаторными задачами люди столкнулись в глубокой древности.
В Древнем Китае увлекались составлением магических квадратов. В Древней Греции занимались теорией фигурных чисел.
Комбинаторные задачи возникли и в связи с такими играми, как шашки, шахматы, домино, карты, кости и т.д. Комбинаторика становится наукой лишь в 18 в. – в период, когда возникла теория вероятности.
Слайд 5
В Древней Греции
подсчитывали число различных комбинаций длинных и
коротких слогов в стихотворных размерах, занимались теорией фигурных чисел,
изучали фигуры, которые можно составить из частей и т.д.
Со временем появились различные игры
(нарды, карты, шашки, шахматы и т. д.)
В каждой из этих игр приходилось рассматривать различные сочетания фигур, и выигрывал тот, кто их лучше изучал, знал выигрышные комбинации и умел избегать проигрышных.
Слайд 6
Готфрид Вильгельм Лейбниц
(1.07.1646 - 14.11.1716)
Комбинаторику, как самостоятельный
раздел математики первым стал рассматривать немецкий ученый Г. Лейбниц в своей работе «Об искусстве комбинаторики», опубликованной в 1666г. Он также впервые ввел термин «Комбинаторика».
Леонард Эйлер(1707-1783)
рассматривал задачи о разбиении чисел, о паросочетаниях, циклических расстановках, о построении магических и латинских квадратов, положил начало совершенно новой области исследований, выросшей впоследствии в большую и важную науку—топологию, которая изучает общие свойства пространства и фигур.
Слайд 7
Для вывода формул автор использовал наиболее простые и
наглядные методы, сопровождая их многочисленными таблицами и примерами. Сочинение
Я. Бернулли превзошло работы его предшественников и современников систематичностью, простотой методов, строгостью изложения и в течение XVIII века пользовалось известностью не только как серьёзного научного трактата, но и как учебно-справочного издания.
Слайд 8
Методы решения комбинаторных задач
Правило суммы.
2.
Правило произведения
3. Таблицы.
4. Графы (деревья).
5. Формулы.
Слайд 9
Правило суммы
Если
элемент А может быть выбран к1 способами, а элемент
В – к2 способами, причем выборы А и В являются взаимно исключающими, то выбор «либо А, либо В» может быть осуществлен к1+к2 способами.
Задача 1. Сколько существует способов выбрать кратное двум или трем число из множества чисел : 2,3,4,15,16,20,21, 75,28 ?
Решение: к1=5 –кратное 2 (2,4,16,20,28),
к2=4 – кратное 3 (3,15,21,75)
к1+к2 = 5+4 = 9
Слайд 10
Правило произведения
Если элемент
А может быть выбран к1 способами, а элемент В
– к2 способами, то выбор «А и В» может быть осуществлен к1хк2 способами.
Задача 2. а) Сколько различных двузначных чисел можно составить из цифр 1,3,5,7,9?
Решение: N= 5х5 = 25 ( Если не сказано, что элемент не повторяется, то выборка с повторениями)
б) Сколько среди них чисел, кратных 5?
Решение: Число кратно 5, если оканчивается цифрой 5 или 0. В нашем случае – 5.
На первой позиции фиксируем одну из пяти цифр, на второй – 5.
N= 5х1 =5
Слайд 11
в) Сколько среди них чисел, кратных 11?
Решение: Двузначное
число кратно 11, если обе его цифры одинаковы. N=
5
г) Сколько среди них чисел, кратных 3?
Решение: Число кратно 3, если сумма его цифр делится на 3. Составим всевозможные пары:
1 -1 3 -3 5 – 5 7 – 7 9 -9
1 -3 3 -5 5 – 7 7 – 9
1 -5 3 -7 5 -9
1 -7 3 – 9
1 – 9
Таких пар 15. Среди них 5 пар, сумма которых делится на 3, причем три пары допускают перестановку, т.е. могут образовать по два разных числа. Всего 5+3=8 различных двузначных чисел.
Правило произведения
Слайд 12
Задача 3. Сколько существует способов занять 1-ое, 2-ое
и 3-е места на чемпионате по футболу, в котором
участвуют
а) 10 команд
Решение: N=10х9х8=720
б) 11 команд?
Решение: N=11х10х9х8=990
Правило произведения
Слайд 13
Задача 4. Сколько различных трехзначных чисел можно составить
из цифр 0, 1,2,3,4, если
а) цифры не повторяются?
Решение:
На первом месте одна из 4-х цифр ( 0 не может быть), на 2-ом – одна из оставшихся 4-х:
N=4х4= 16
б) цифры могут повторяться
Решение: На 1-ом месте может быть одна из 4-х цифр, на 2-ом – одна из 5 (0 входит):
N=4х5= 20
Правило произведения
Слайд 14
Правило произведения
Задача 5. Несколько стран в качестве символа
своего государства решили использовать флаг в виде четырех горизонтальных
полос, одинаковых по ширине, но разных по цвету: белый, синий, красный, зеленый. У каждой страны свой, отличный от других, флаг.
а)Сколько всего стран могут использовать такую символику?
Решение: Цвет верхней полосы можно выбрать одним из 4 способов, второй полосы – одним из трех оставшихся, цвет 3 полосы – одним из 2 оставшихся, а 4 – одним способом. По правилу произведения N=4х3х2х1=24
Слайд 15
б) Сколько стран могут использовать такую символику с
синей и красной полосами, расположенными рядом?
Решение: Две полосы, всегда
расположенные рядом, можно рассматривать как одну полосу, тогда полос останется 3, из них можно составить 3х2х1=6 разных флагов. Но две полосы (синюю и красную) можно «склеить» по-разному: синяя, а под ней красная, или красная, а под ней синяя. Поэтому общее количество вариантов по правилу суммы равно 6+6=12
Правило произведения
Слайд 16
в) Сколько всего стран могут использовать такую символику
с нижней белой полосой?
Решение: Если фиксировать цвет нижней полосы,
то цвета трех расположенных над ней полос можно выбрать 3х2х1 = 6 способами
Правило произведения
г) Сколько стран могут использовать такую символику с верхней белой полосой?
Решение: Если фиксировать цвет белой полосы, то цвета следующих полос можно выбрать 3х2х1 = 6 способами.
Слайд 17
Правило произведения
Задача 6. В клетки квадратной таблицы 2х2
произвольно ставят крестики и нолики.
а) Сколькими способами можно заполнить
эту таблицу?
Решение: Для заполнения первой клетки есть 2 способа ( крестик или нолик); для заполнения каждой последующей – тоже 2 способа; общее количество способов заполнить таблицу по правилу произведения равно 2х2х2х2=16.
Слайд 18
Правило произведения
б) В скольких случаях в
верхней левой и нижней правой будут разные значки?
Решение: Если
в верхней клетке – крестик, а нижней – нолик, то остальные клетки можно заполнить 2х2=4 способами. Если в верхней клетке – нолик, в нижней – крестик, то еще 4 способа заполнения. Всего 4+4=8 способов.
Слайд 19
Правило произведения
в) В скольких случаях в левой нижней
клетке будет стоять крестик?
Решение: Если в левой нижней клетке
фиксируем крестик, то остальные 3 клетки можно заполнить 2х2х2=8 различными способами
Слайд 20
Правило произведения
Задача 7. Сколькими способами можно посадить
шестерых школьников на скамейку так, чтобы Коля и Оля
оказались рядом?
Решение: Будем считать, что на скамейке 6 пустых мест. Посадить Колю можно шестью способами, после чего Олю посадить рядом с ним одним или двумя способами. Это зависит от того, куда мы посадили Колю – на крайнее место или нет.
Слайд 21
Правило произведения
Пусть Коля сидит на краю. Место на
краю можно выбрать 2 способами, после чего Олю можно
посадить одним способом, после чего оставшиеся 4 места можно занять 4х3х2х1 способами, значит, всего 2х1х4х3х2х2=48 способов
Коля сидит где-то в середине. Место для Коли можно выбрать 4 способами, Олю можно посадить 2 способами, значит, всего
4х2х4х3х2х1=192 способами.
По правилу сложения 48+192= 240 способов
Слайд 22
Правило произведения
Задача 8. Из цифр 1,2,3,5 составили все
возможные четырехзначные числа (без повторения цифр). Сколько среди них
таких чисел, которые больше 2000, но меньше 5000?
Решение: Выбор 1-ой цифры – 2 способа (3,4), 2-ой цифры – 3 способа, третьей – 2 способа, четвертой -1. По правилу произведения N=2х3х2х1=12 чисел.
Слайд 23
Правило произведения
Задача 9. На входной двери дома установлен
домофон, на котором нанесены цифры 0,1,2,…9.Каждая квартира получает кодовый
замок из двух цифр типа 0-2, 3-7 и т.п. Хватит ли кодовых замков для всех квартир, если в доме 96 квартир? (код 0-0 не существует)
Решение: Выбор 1-й цифры – 10 вариантов, 2-й –10 вариантов.
Всего 10х10 – 1 = 99 вариантов
Ответ: хватит.
Слайд 24
Правило произведения
Задача 10. В контрольной работе будет 5
задач – по одной из каждой пройденной темы. Задачи
будут взяты из общего списка по 10 задач в каждой теме, а всего было пройдено 5 тем. При подготовке к контрольной работе Вова решил только по 8 задач в каждой теме. Найдите:
а) общее число всех возможных вариантов контрольной работы
Решение: Каждая задача может быть выбрана 10 способами. По правилу произведения N=10х10х10х10х10=100000
Слайд 25
Правило произведения
б) число тех вариантов, в которых Вова
умеет решать все 5 задач
Решение: N=8х8х8х8х8=32768
в) число тех вариантов,
в которых Вова не сможет решить ни одной задачи
Решение: N=2х2х2х2х2=32
г) число тех вариантов, в которых Вова умеет решать все задачи, кроме первой.
Решение: N=2х8х8х8х8=8192
Слайд 26
Правило произведения
Задача 11. Три вершины правильного 10-угольника покрасили
в рыжий цвет, а остальные – в черный. Сколько
можно провести отрезков с разноцветными концами?
Решение: Первую рыжую вершину можно соединить отрезком с любой из 10 – 3 = 7 черных вершин, после этого вторую рыжую вершину можно соединить отрезком с любой из 6 оставшихся черных вершин, а третью рыжую – с любой из 5 оставшихся черных вершин. Общее число вариантов (отрезков с разноцветными концами) по правилу произведения равно:
7х6х5=210
Слайд 27
Правило произведения
Задача 12. Сколько ребер имеет полный граф
(каждая вершина соединена с каждой), если количество его вершин
12?
Решение: Первую вершину можно выбрать из 12, вторую – из 11; всего 12х11=132 пары. Но они учитывают порядок выбора (каждая пара входит дважды). Поэтому количество ребер равно 12х11:2=66
Слайд 28
Таблицы вариантов
Задача 13
Составляя расписание уроков
на понедельник для 7а класса, завуч хочет первым уроком
поставить либо физику, либо алгебру, а вторым – либо русский язык, либо литературу, либо историю. Сколько существует вариантов составления расписания на первые два урока?
Решение: Составим таблицу вариантов:
Всего существует 2х3 = 6 вариантов
Слайд 29
Таблицы вариантов
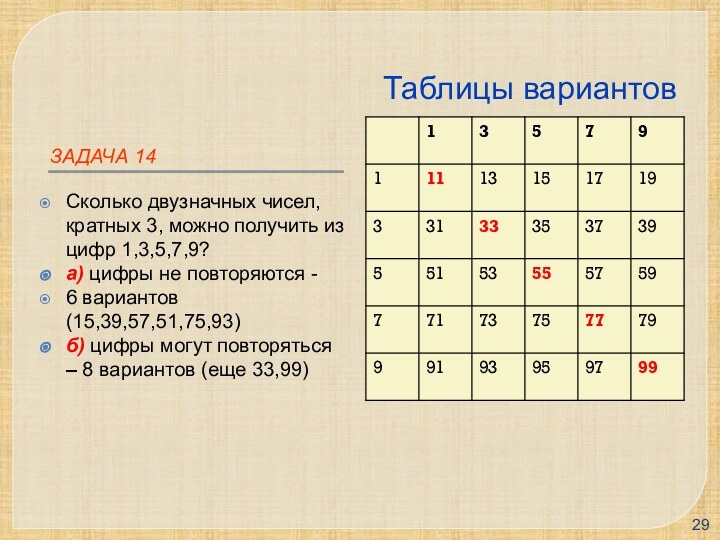
Задача 14
Сколько двузначных чисел, кратных 3, можно
получить из цифр 1,3,5,7,9?
а) цифры не повторяются -
6 вариантов
(15,39,57,51,75,93)
б) цифры могут повторяться – 8 вариантов (еще 33,99)
Слайд 30
Подсчет вариантов с помощью графов
Задача 15. При встрече
каждый из друзей пожал другому руку. Сколько было рукопожатий,
если друзей:
а) трое ; б) четверо ; в) пятеро?
N=3 N=6 N=10
Слайд 31
Подсчет вариантов с помощью графов
Задача 16. По окончании
деловой встречи специалисты обменялись визитными карточками. Сколько всего визитных
карточек было роздано, если специалистов было
а) трое ; б) четверо ; в) пятеро?
N=3 N=6 N=10
Слайд 32
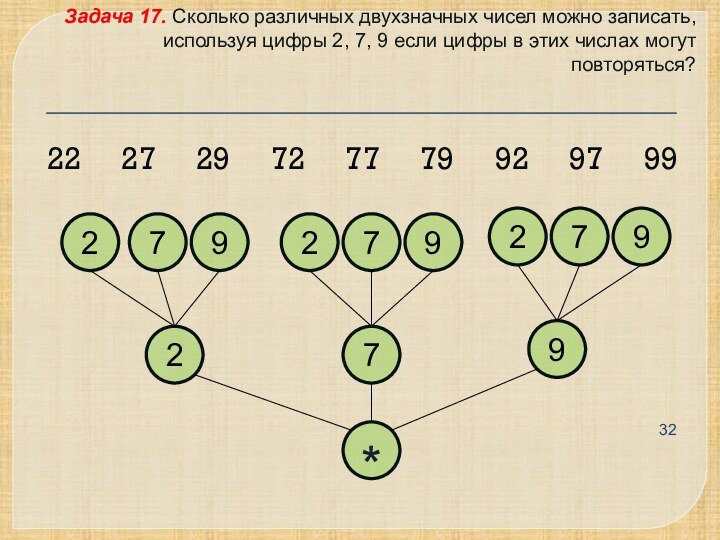
Задача 17. Сколько различных двухзначных чисел можно записать,
используя цифры 2, 7, 9 если цифры в этих
числах могут повторяться?
22 27 29 72 77 79 92 97 99
2
7
9
9
7
2
2
9
7
9
7
2
*
Слайд 33
Граф-дерево
Задача 18. Маше на день рождения подарили 3
букета цветов: из роз (р), астр (а) и гвоздик
(г). В доме было 2 вазы: хрустальная (х) и керамическая (к). Маша пробовала устанавливать каждый букет в каждую вазу. Перечислить все полученные сочетания букета с вазой.
Слайд 34
Виды выборок
Перестановки без повторений
Размещения без повторений
Сочетания без повторений
Размещения с повторениями (строки)
Перестановки с повторениями
Сочетания с
повторениями
Разбиения
Подмножества
Слайд 35
Формулы комбинаторики
Факториал числа - произведение n первых натуральных
чисел обозначается n!
5!=1*2*3*4*5=120; n!=1*2*3*…*(n-1)*n
Перестановка без повторений.
Задача 19. Даны цифр:
1,2,3,4,5,6,7. Сколько различных чисел можно составить из этих цифр? Каждое число является перестановкой из 7 элементов.
Примеры: 1234567, 2354167, 7546321.
Перестановка-упорядоченное множество.
Число перестановок из n элементов вычисляют по формуле Pn=n!.
По условию n=7
Так из 7 цифр можно 7!=1*2*3*4*5*6*7=5040 различных чисел.
Слайд 36
Формулы комбинаторики
Перестановка с повторениями.
Задача 20 .Даны цифр: 1,2,2,3,3,3,4,.
Сколько различных чисел можно составить из этих цифр? Каждое
число является перестановкой из 7 элементов.
Примеры: 1223334, 4232331,2233314.
Некоторые числа при перестановке одинаковых цифр не меняется. Число таких перестановок вычисляется по формуле Pn=n!/(n1!*n2!*n3!).
По условию n=7, n1=2 , n2=3
Получаем 7!/(2!*3!)=5040/12=420 различных чисел.
Слайд 37
Формулы комбинаторики
Сочетание.
Задача 21. Имеется
7 цветных карандашей. Выбирается 3 карандаша. Сколько существует способов
выбрать 3 карандаша, чтобы не было повторяющихся наборов? Выборка из трёх карандашей – это сочетание из 7-ми по 3 элемента в каждом.
Сочетание - неупорядоченная выборка.
Число сочетаний из n элементов по m в каждом находим по формуле: Cn = n!/(m!*(n-m)!).
Решение: 7!/(4!*3!)=7*6*5=210
Задача 22. В классе обучается 20 человек. Сколько существует способов выбрать актив, состоящий из 4 человек?
Решение. Находим число сочетаний из 20 элементов по 4 в каждом: 20!/(4!*16!)=17*18*19*20/24=4845 способов выбрать актив.
Слайд 38
Формулы комбинаторики
Размещение.
Задача
23. Буквы алфавита записаны на карточках. Выбирается 4 карточки
и затем из набора составляют различные слова. Под словом будем понимать порядок следования букв. Например:
плот, лотп, лпот- разные слова. Каждое полученное слово-это размещение.
Размещение –упорядоченная выборка
Число размещений из n элементов по m в каждом находим по формуле: An =n!/(n-m)!.
Сколько слов можно получить в предложенной задаче? По формуле получаем решение
32!/(32-4)!=32!/28!=29*30*31*32=863040