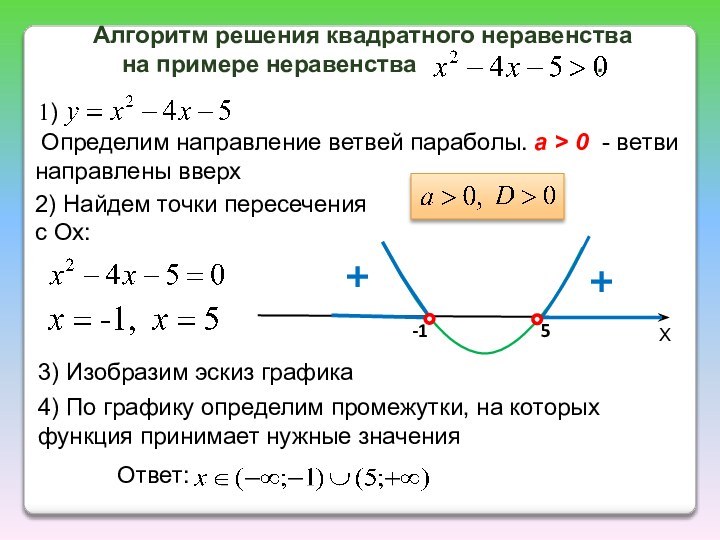
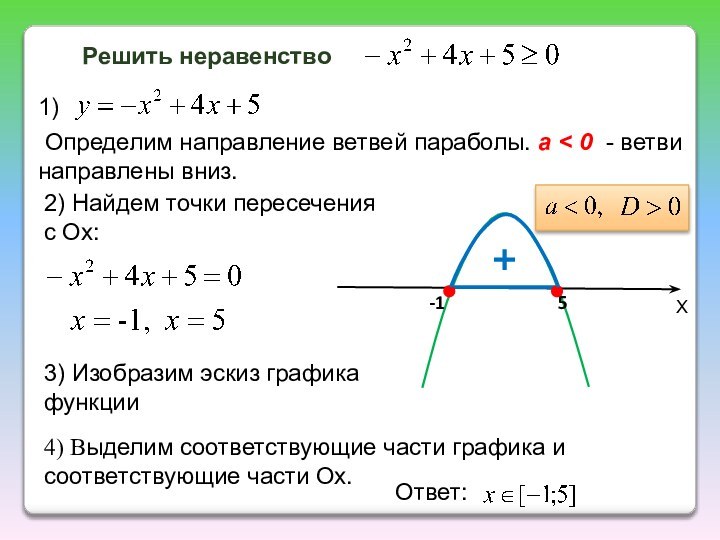
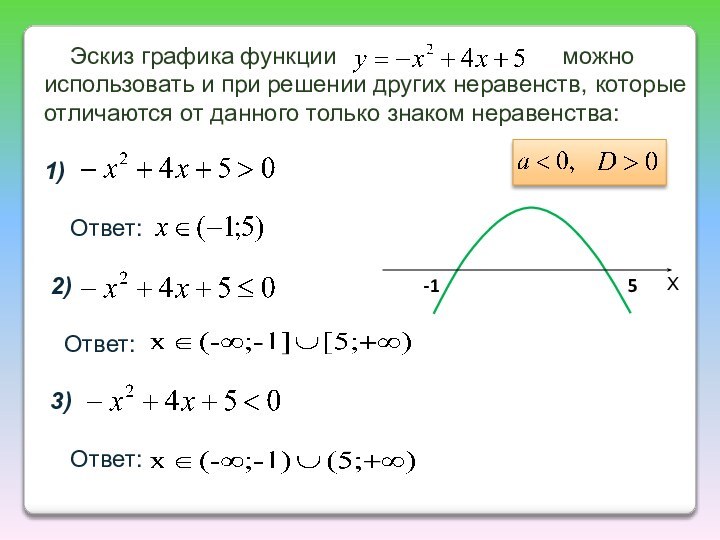
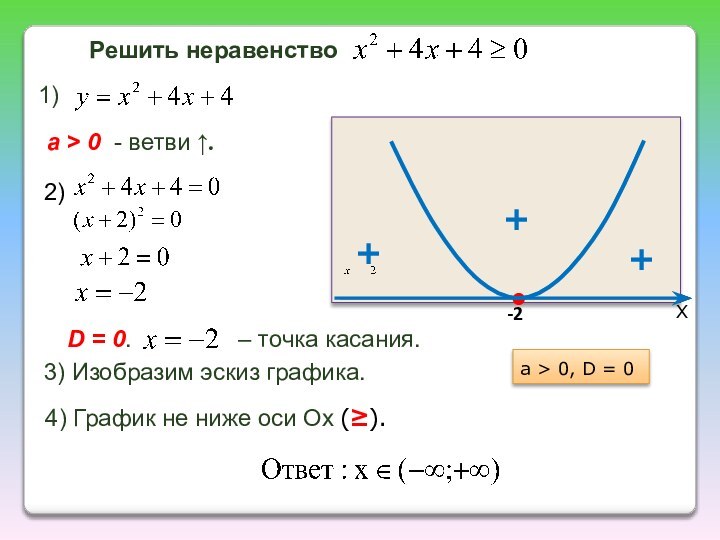
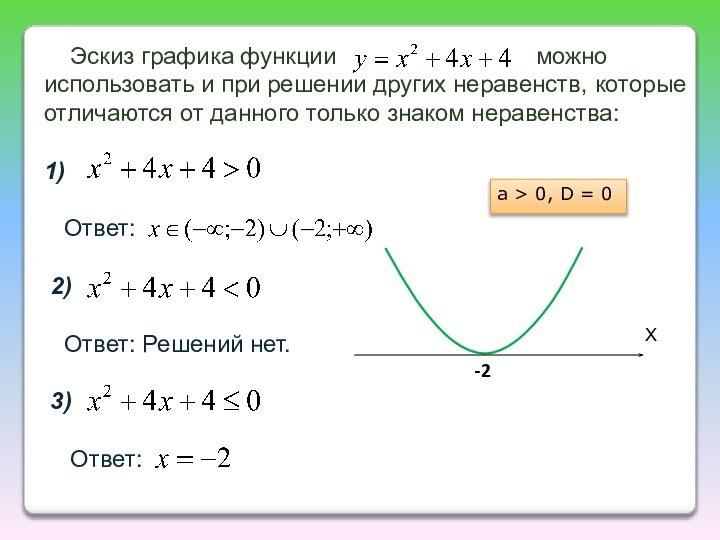
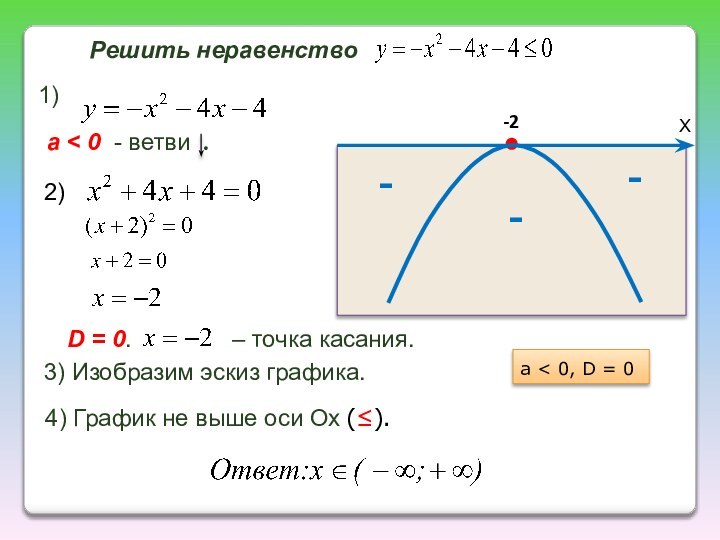
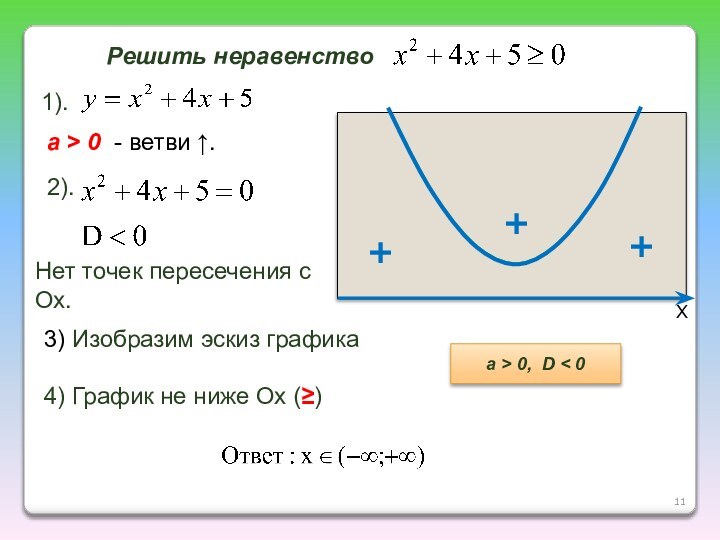
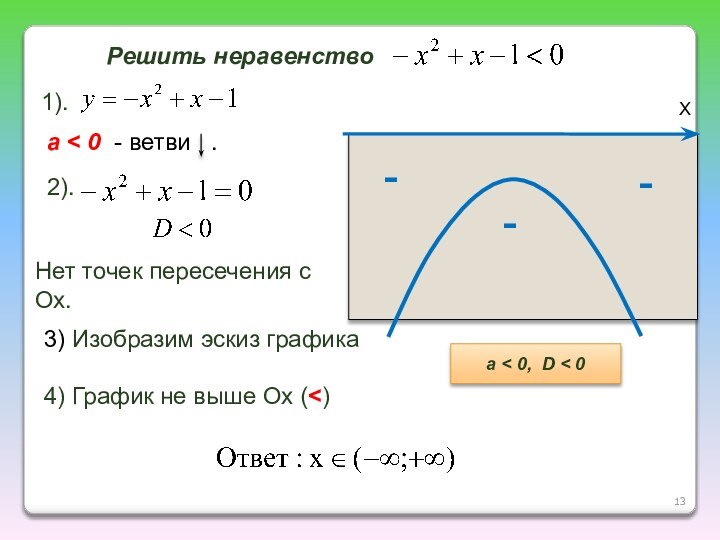
ветвей параболы по знаку первого коэффициента квадратичной функции;
найти действительные
корни соответствующего квадратного уравнения или установить, что их нет;изобразить эскиз графика квадратичной функции, используя точки пересечения (или касания) с осью Ох, если они есть;
по графику определить промежутки, на которых функция принимает нужные значения.