Слайд 2
Решение нестандартных задач
Слайд 3
Какая же задача называется нестандартной? «нестандартные задачи –
это такие задачи, для которых в курсе математики не
имеется общих правил и положений, определяющих их решение» (Фридман Л.Н. Как научиться решать задачи).
Однако понятие «нестандартная задача» относительное. Одна и та же задача может быть и стандартной и нестандартной, в зависимости от того, знаком ученик с задачами такого типа или нет.
Слайд 4
Таким образом, нестандартная задача – это
задача, алгоритм решения которой учащемуся неизвестен. Для решения таких
задач мы выделили 4 ступени:
1.изучение условия задачи
2.поиск плана решения
3. осуществление плана, т.е. оформление найденного решения
4.изучение полученного решения – критический анализ результата и отбор полезной информации.
Слайд 5
Идея создания проекта:
просмотрев задания олимпиад за
несколько прошлых лет, я поняла, что не могу их
так сразу решить, но убедилась, что это задачи нестандартного типа. Я попытались классифицировать их и разбила на несколько групп.
Цель данного проекта: научиться решать олимпиадные задачи определённого типа
Слайд 6
В связи с этим можно выделить следующие
задачи проекта:
составить подборку задач по теме: задачи на
делимость многозначного числа на натуральное
решить эти задачи различными способами
использовать вспомогательные задачи
попытаться научиться составлять вспомогательные задачи
использовать метод полной индукции (метод перебора всех возможных случаев), метод неполной индукции (рассмотрение некоторых частных примеров) и решение в общем виде – дедукции
закрепить признаки делимости
Слайд 7
Я попытаюсь изложить материал так, чтобы
он стал доступен и понятен и другим учащимся, для
этого выступлю на элективных курсах, на конференции. В своём проекте я постараюсь показать ход действий, направление мысли при решении одной интересной задачи. Во что вылились наши поиски, исследования, вы и увидите в этом проекте
Слайд 8
При просмотре олимпиадных заданий мы столкнулись с такой
задачей:
* Дано многозначное число авс….kxyz. Отделив от него
трёхзначное число, образованное последними цифрами, получим два числа авс….k и xyz. Доказать, что если разность полученных чисел делится на 7 (11, 13), то и данное число делится на 7 (11, 13)
Слайд 9
Решить сразу эту задачу я не смогла,
тогда учительница предложила решить
вспомогательную задачу
Слайд 10
**В шестизначном числе 1-я цифра совпадает с 4-й,
2-я с 5-й, 3-я с 6-й. Докажите, что это
число кратно 7, 11, 13
Я не смогла найти подход к этой задаче, пришлось изучить некоторые основные понятия, условности, обозначения по этой теме, затем прорешать задачи повышенной сложности из учебника алгебры 7 класса
Слайд 11
Основные понятия
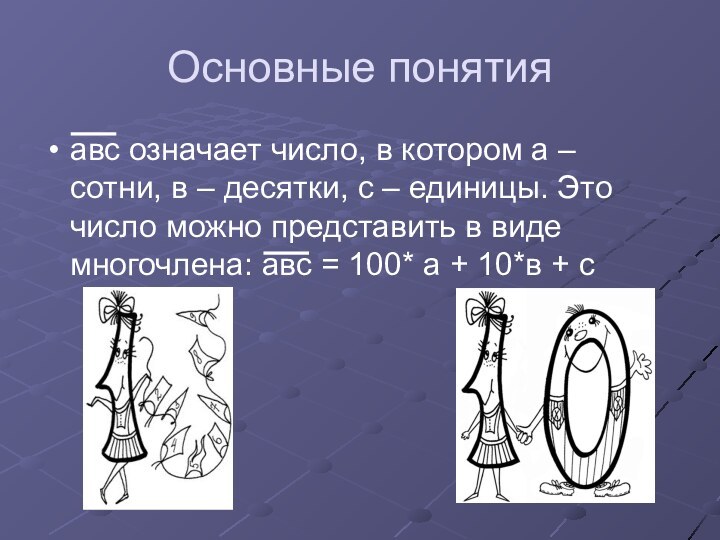
авс означает число, в котором а –
сотни, в – десятки, с – единицы. Это число
можно представить в виде многочлена: авс = 100* а + 10*в + с
Слайд 12
Закрепим на примерах
1.Представим в виде многочлена:
а) ху =
10х+у
б) ух = 10у+х
в) аов = 100а + 10о
+ в
г) авсd = 1000а + 100в + 10с + d
Слайд 13
2.Представьте в виде многочлена и упростите его:
а)
авс + сва = 100а + 10в + с
+ 100с + 10в + а = 101а + 20в + 101с
б) авс + вс = 100а + 10в + с + 10в + с = 100а +20в + 2с
в) авс – ва = 100а + 10в +с – 10в – а = 99а + с
г) авс – ас = 100а + 10в + с – 10а - с = 90а + 10в
Слайд 14
3. Доказать что:
а) Сумма
чисел ав + ва кратна сумме (а + в).
Представим в виде многочлена: 10а + в + 10в + а = 11а + 11в = 11(а+в) т.к один из множителей делится на (а+в), то и все произведение делится на (а+в)
б) Разность чисел ав – ва кратна 9
Представим в виде многочлена: ав – ва = 10а + в – 10в – а = 9а – 9в = 9(а-в) т.к один из множителей делится на 9, то и все произведение кратно 9.
Слайд 15
Задача
Доказать, что
если к двузначному числу прибавить число оканчивающееся теми же
цифрами, но в обратном порядке, то полученная сумма будет кратна 11. Выполняется ли свойство для
трехзначных чисел?
Слайд 16
РЕШЕНИЕ:
ав+ва = 10а + в +
10в + а = 11а+11в = 11 ( а+в)
число кратно 11
Попробуем использовать этот же алгоритм для трехзначных чисел.
авс +сва = 100а +10в+с+100с+10в+а= 101а+20в+101с свойство не выполняется. Число не делится на 11
Слайд 17
Вернёмся к вспомогательной задаче **
Обозначим
1ц – а, 2я – в, 3я – с
, тогда число авсавс= 100000а + 10000в + 1000с + 100а + 10в + с =1000 ( 100а + 10в + с ) + авс = 1000авс + авс = 1001авс = 11*7*13 авс кратно 7,11,13
Слайд 18
Вернёмся к первоначальной задаче *
авс…к -xyz = ?
Сначала я никак не
могла расписать разность, но потом я поняла, что разность делится на 7 авс…к xyz = 1000 ( авс…к ) + xyz = 1000 авс…к + авс…к – авс…к + xyz = 1001 авс…к + ( xyz – авс…к) скобка уже делится на 7 , то и число 1001 тоже делится на 7, т.к каждое слагаемое делится на 7, то и вся сумма делится на 7 ( признак делимости суммы)
Теперь мы можем сами вывести признак делимости на 7,11,13
Слайд 19
ГИПОТЕЗА!
Если разность между самим многозначным числом
и числом, состоящим из 3х последних цифр, делится на
7,11,13, то и все число делится на 7,11,13
НАПРИМЕР: 235 123 Вычтем из самого числа меньшее число и разность разделим на 7
235 – 123 = 112 : 7 = 16
Проверим делится ли само число на 7. Число делится!
А, например, число 234123 не делится на 7.
(проверено на10 примерах)
Слайд 20
Решив данную задачу, стало интересно, можно
ли этот подход применить к другим подобным задачам, например
таким:
Слайд 21
Задача. Найти двузначное число, которое в 4 раза
больше суммы его цифр
Решение: (1 способ) пусть само число
ав = 10а + в, 0 а 9, 0 в 9
По условию задачи составим уравнение
10а + в = 4 ( а + в )
6а = 3в
2а = в
в этом уравнении нужно решать с помощью подбора , учитывая что а,в – цифры ( использовать метод полной индукции)
Если а = 1 то в = 2, т.е число = 12
а = 2 то в = 4 т.е число = 24
а = 3 то в = 6 т.е число = 36
а = 4 то в = 8 т.е число = 48
а = 5 то в = 10 такого быть не может т.к в не должно быть больше 9
ОТВЕТ: 12, 24,36,48
Слайд 22
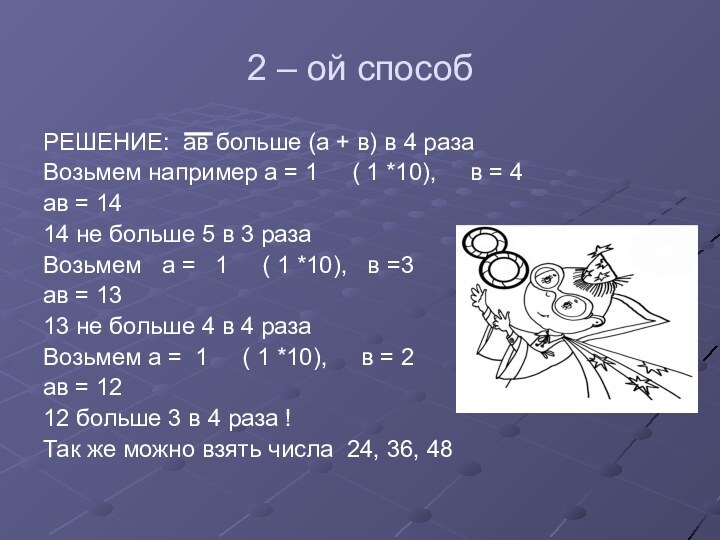
2 – ой способ
РЕШЕНИЕ: ав больше (а +
в) в 4 раза
Возьмем например а = 1
( 1 *10), в = 4
ав = 14
14 не больше 5 в 3 раза
Возьмем а = 1 ( 1 *10), в =3
ав = 13
13 не больше 4 в 4 раза
Возьмем а = 1 ( 1 *10), в = 2
ав = 12
12 больше 3 в 4 раза !
Так же можно взять числа 24, 36, 48
Слайд 23
ЗАДАЧА
К некоторому двузначному числу слева и
справа приписали по 1. В результате получили число, в
23 раза больше первоначального. Найти это двузначное число.
РЕШЕНИЕ1: 1*ав*1=23*ав ав=10а+в
1000+10ав+1=23ав
1001=13ав
ав=77
Ответ:77
Слайд 24
РЕШЕНИЕ (способ 2):
1ав1=23ав
Вместо в должно быть число
7 т.к 3*7= ( а 1ав1 заканчивается
1)
1а71=23 а7
1000+100а+10в+1=230а+23в
130а+13в=1001
130а+13*7=1001
130а=910
а=910/130
а=7 а - десятки, в – единицы ав=77
ответ:77
Слайд 25
ЗАДАЧА
Если к задуманному числу справа приписать
0 и результат вычесть из числа 143, то получится
утроенное задуманное число. Какое число задумано?
РЕШЕНИЕ: 143 – хо=3*х
Если х - однозначное, то хо – двузначное число
143-10х-о=3х
143=13х
Х=11 ( задуманное число)
Если х – двузначное число, то хо – трехзначное
143-100х-о=3х
143=103х
Х=1 (приблизительно) (ВАРИАНТ не подходит)
Слайд 26
Вспомогательные задачи
( придуманные мною)
1.
К числу х приписали справа цифру 3, представить полученное
число в виде суммы, если х а)двузначное число б)трёхзначное число
2. К числу у приписали слева цифру 7, представить полученное число в виде суммы, если у а)двузначное число б)трёхзначное число
Слайд 27
Рефлексия
Мне очень понравилось работать с этим типом
задач ( разложение на множители в виде разрядных слагаемых).
Эти задачи не просты в решении, поэтому к ним нужен особый подход. Может поэтому они мне очень понравились. Тем более эти задачи помогут при подготовке и проведении олимпиадных задач. В дальнейшем я хочу разобраться в решении задач со степенями
Слайд 28
Литература
Энциклопедический словарь юного математика/Составитель Э-68 А.П.Савин,-М., Педагогика,1989
Алгебра, 7класс.
Под редакцией С.А. Теляковского