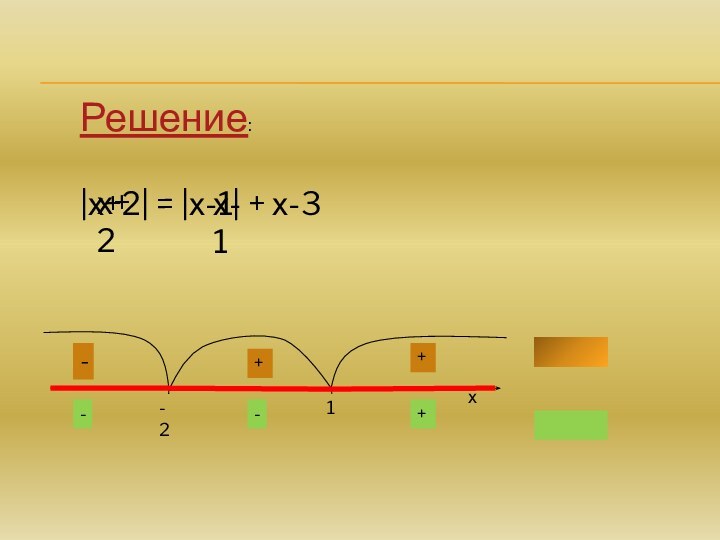
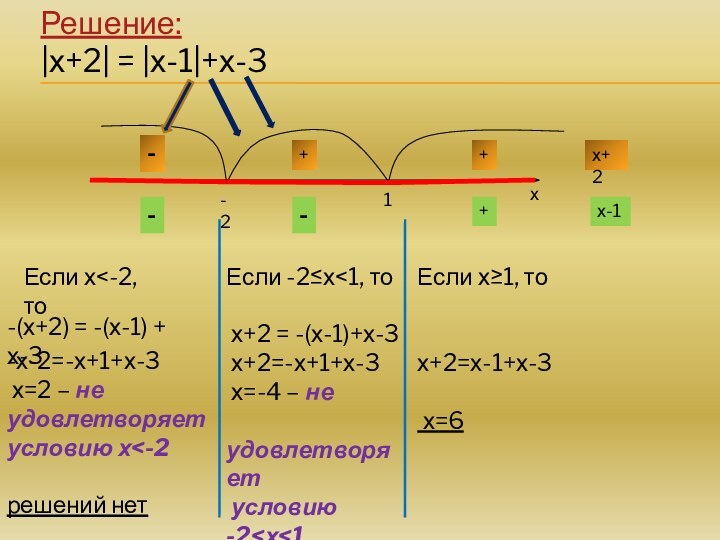
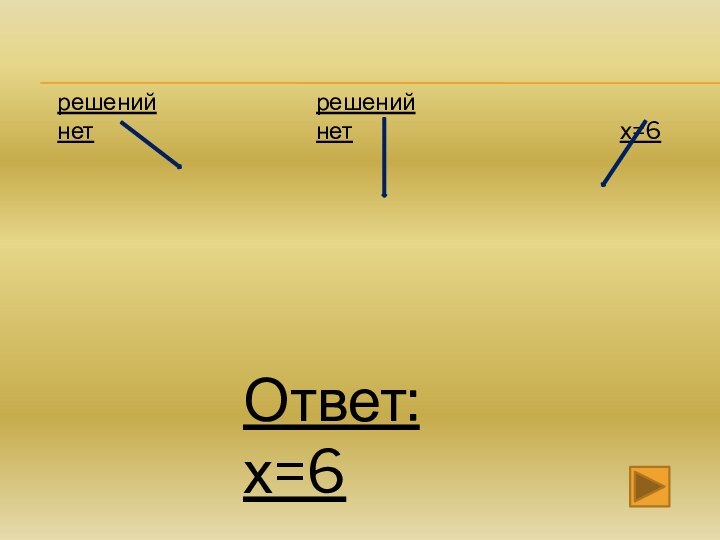
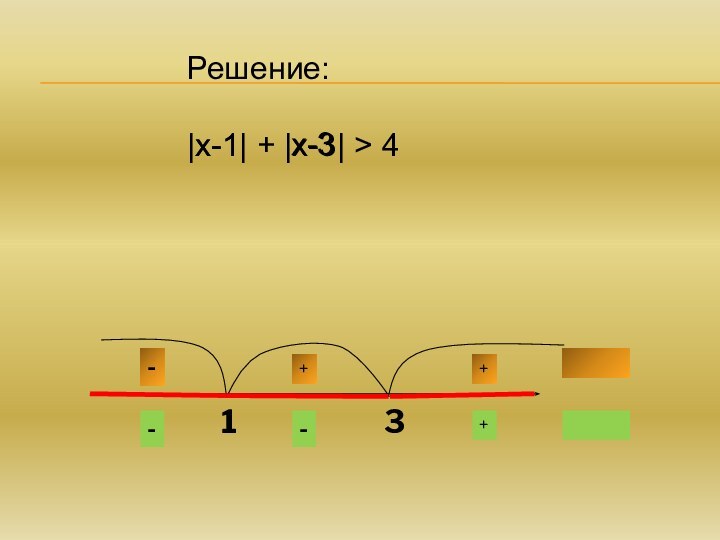
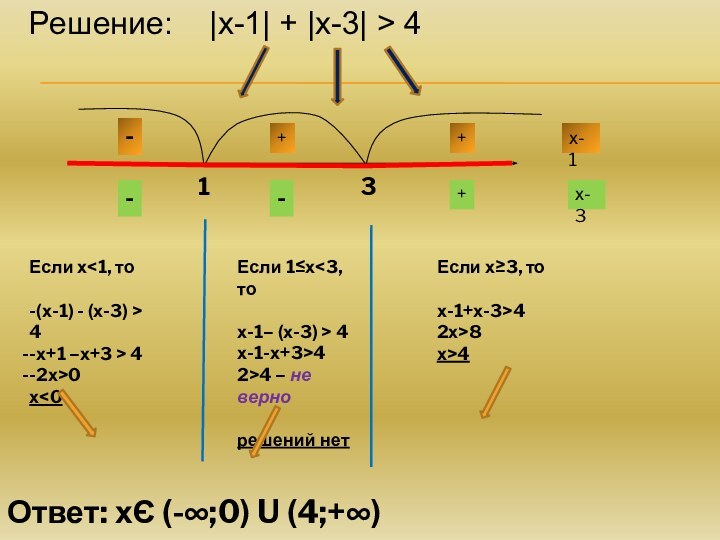
само это число, если а – положительное число;
нуль, если
число а – нуль;число, противоположное а , если число а – отрицательное.
Или
а, если а>0
0, если а=0
-а, если а<0
|а| =
Определение модуля