Презентация на тему Решение задач координатным методом

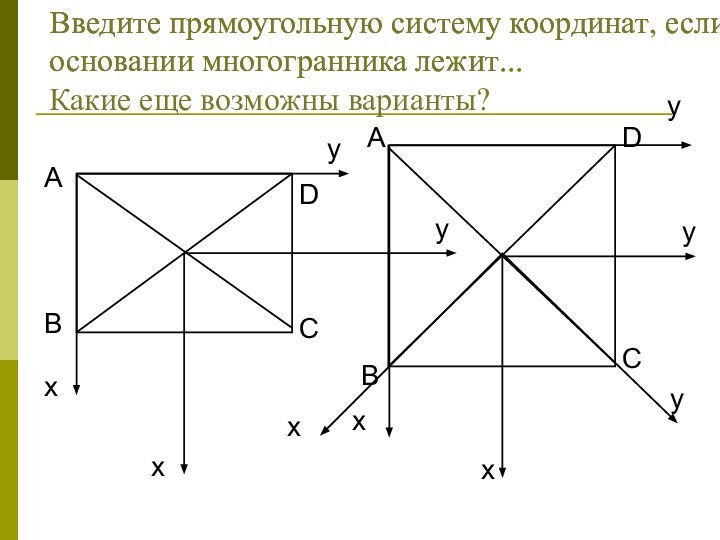
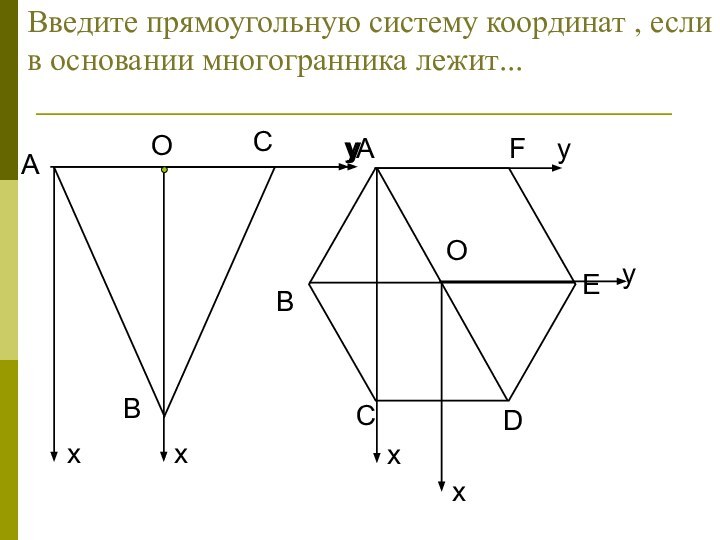
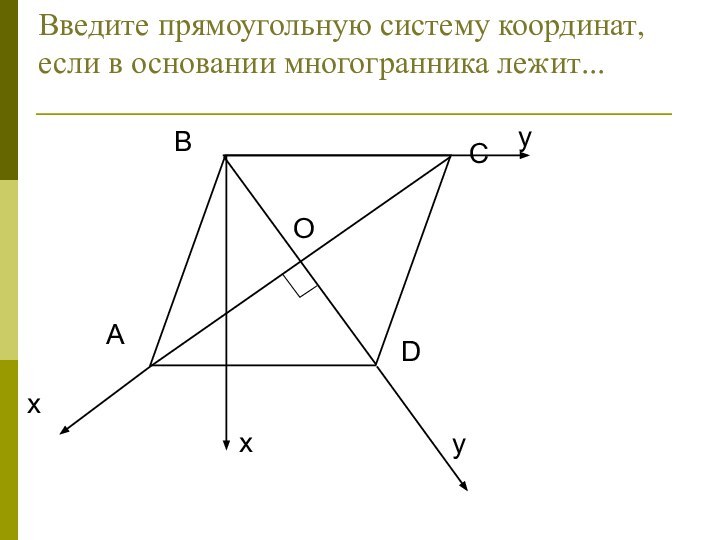
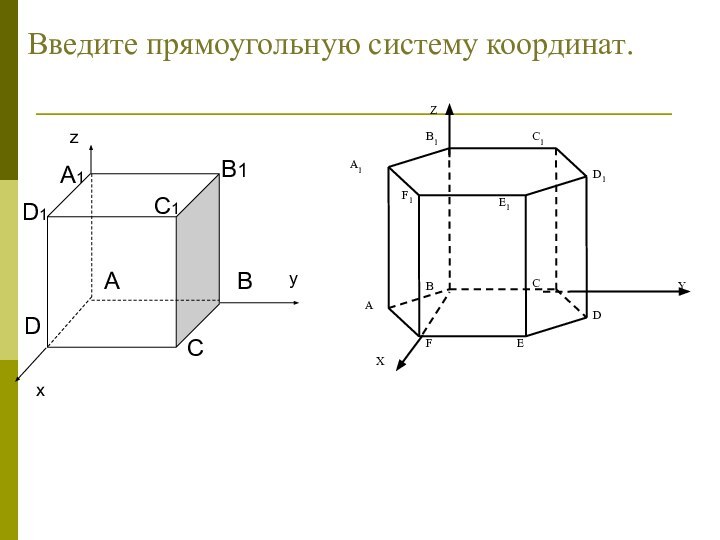
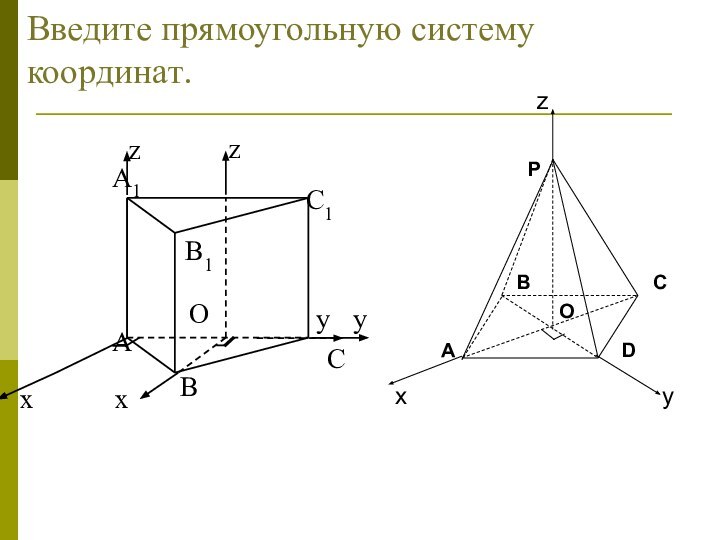
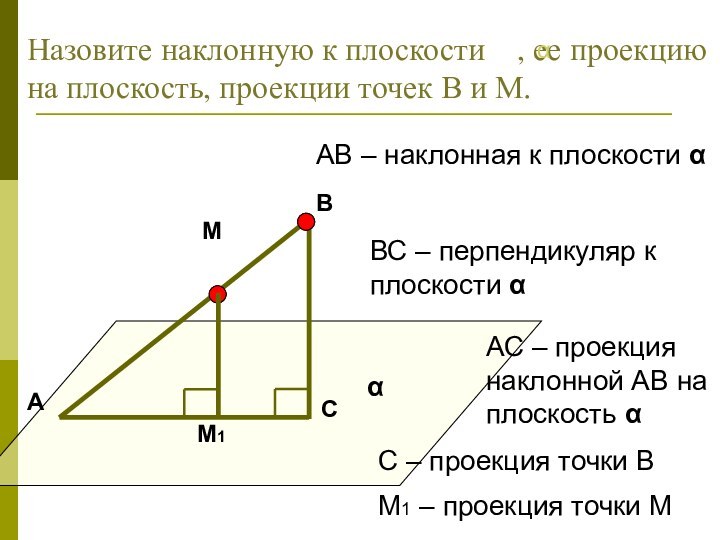
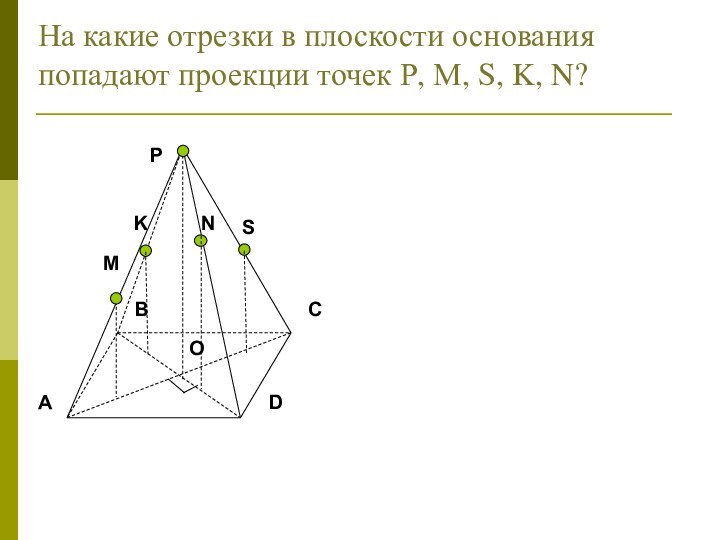
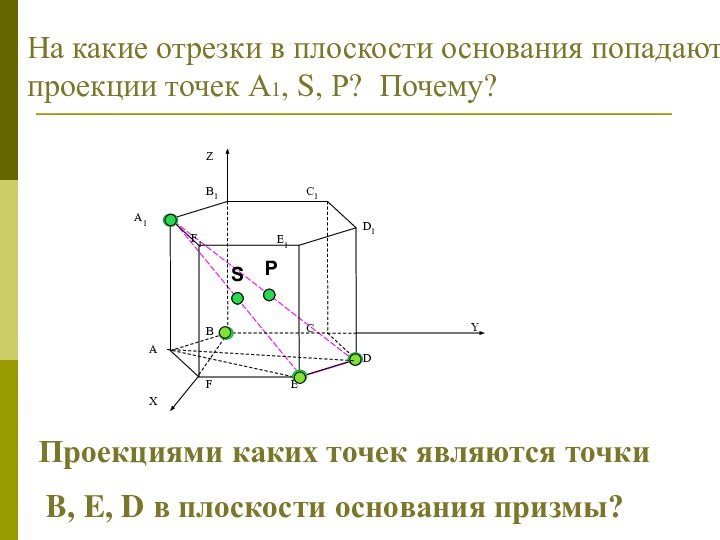
координатах :
Условие коллинеарности двух векторов.
Условие перпендикулярности двух векторов.
Формулу для

нахождения косинуса угла между векторами.
Формулу для нахождения длины вектора.
Уравнение плоскости.

Ответы для самопроверки математического диктанта

- на плоскости основания многогранника; - в пространстве.
Найти координаты точек, о которых идет речь в условии задачи.
Найти координаты - направляющих векторов прямых; - векторов, перпендикулярных плоскостям (нормалей).
Воспользоваться соответствующей формулой для нахождения - расстояний в пространстве; - углов в пространстве.

лежит...
Введите прямоугольную систему координат, если в основании многогранника лежит... Какие

еще возможны варианты?

многогранника лежит...

лежит...
A
B
C
D
O

АВ – наклонная к плоскости α
ВС – перпендикуляр

к плоскости α

С – проекция точки В

α

М

М1

Назовите наклонную к плоскости , ее проекцию на плоскость, проекции точек В и М.

α

М1 – проекция точки М

точек Р, М, S, K, N?
N
K
S

точек А1, S, Р? Почему?
Проекциями каких точек являются точки

B, E, D в плоскости основания призмы?

равна 3, на диагоналях граней АD1 и D1В1 взяты

точки Е и К так, что D1Е:АD1=1:3, D1K:D1B1=2:3. Найдите длину отрезка DK.

Решение.

равны 1. Найдите расстояние от точки В до точек Е1, D1.
y
x

Найдите расстояние от точки В до плоскости DEA1.
y
x

ребра которой равны 1, найдите расстояние между прямыми АА1

и ВС1. Решение.

Расстояние между скрещивающимися прямыми равно расстоянию от точки на одной прямой до плоскости, содержащей вторую прямую и параллельной первой прямой.

1. Введем систему координат с началом в точке О, как показано на рисунке.

Найдем расстояние от точки А до плоскости ВСС1

(PRS) и (NKM), ребро которого 12, где DN:NC=A1P:PB1=1:2, B1S:SB=D1M:MD1=1:3,

B1R:RC1=DK:KA=1:4. Решение.

1. Введем прямоугольную систему координат
с началом в точке В, как показано на рисунке.

2. В(0; 0; 0); P(6; 0; 12); R(0; 3; 12);
S(0; 0; 8); N(6; 12; 0); K(12; 9; 0); M(12; 12; 4)

3. Уравнение плоскости (PRS) имеет вид 2x+4y-3z+24=0, а уравнение плоскости (NKM) 2x+4y-3z-60=0,
значит, плоскости параллельны.

что CE:EC1=2:1 . Найдите угол между прямыми  BE и AC1 .

равны 1, боковые ребра равны 2, точка D — середина ребра CC1 Найдите

угол между плоскостями ABC и ADB1.

с вершиной Р равны между собой. Найдите угол между

прямой ВМ и плоскостью BDP, если точка М – середина бокового ребра пирамиды АР.

ABCD со стороной , а

угол BAD равен 60°. Найти расстояние от точки А до прямой С1D1, если боковое ребро параллелепипеда равно 8.

1. Как введем прямоугольную систему координат?

Т.к. диагонали ромба перпендикулярны,
то начало координат можно взять в точке их пересечения.

2. Координаты каких точек надо найти?

А, С1, D1 и основания перпендикуляра, опущенного из точки А на прямую С1D1 – точки К1.

Где лежит проекция точки К1?

На прямой СD.

Пусть К1(х0,у0,z0), ее проекция К(х0,у0,0)

ABCD, со стороной , а

угол BAD равен 60°. Найти расстояние от точки А до прямой С1D1, если боковое ребро параллелепипеда равно 8.

Найдем остальные координаты точки К1.

кубе ABCDA1B1C1D1 точки E и K – середины
ребер

AA1 и CD соответственно, а точка M расположена на диагонали B1D1 так, что B1M=2MD1. Найти расстояние между точками Q и L, где Q – середина отрезка ЕМ, а L – точка отрезка МК такая, что ML=2LK.

1. Ребра правильной четырехугольной призмы равны 1, 4, 4. Найти расстояние от вершины до центра основания призмы, не содержащего эту вершину.

2. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все рёбра равны 1. Найдите расстояние от точки В до точек Е1, D1.

№ 484559, 484569, 485992, 485997, 500007, 500193, 500367 на сайте http://reshuege.ru