- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Решение задач на нахождение площади
Содержание
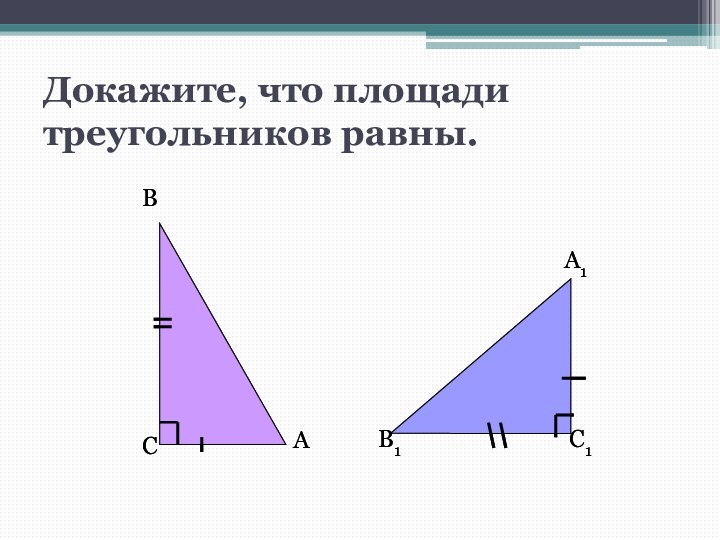
- 2. Докажите, что площади треугольников равны.
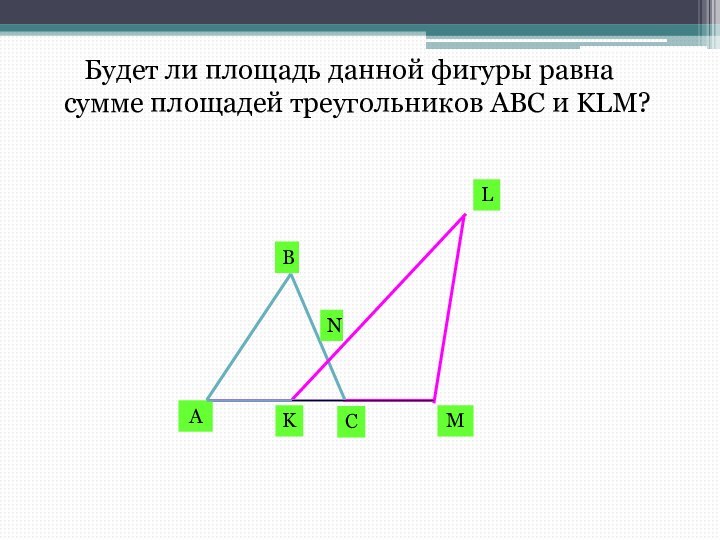
- 3. Будет ли площадь данной фигуры равна сумме площадей треугольников АВС и KLM?ABCKLMN
- 4. Свойства площадей многоугольниковРавные многоугольники имеют равные площади.Если
- 5. Повторим формулы площадейSквадрата = а·а = а²S = а·b dSквадрата =0,5 d²d
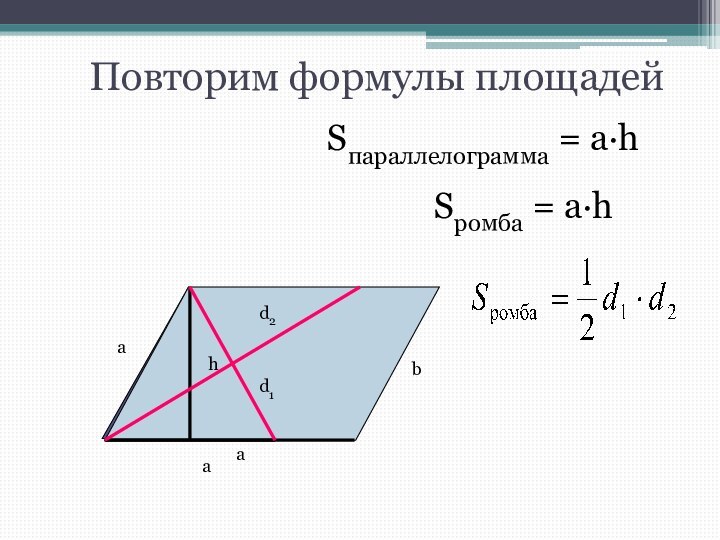
- 6. Повторим формулы площадейhSпараллелограмма = а·h аSромба = а·h а
- 7. Повторим формулы площадей
- 8. В прямоугольном треугольнике
- 9. 8510В прямоугольном треугольнике а и b
- 10. Дано: ∆ ABC,
- 11. Диагонали ромба равны 12 см и 16
- 12. Площадь прямоугольной трапеции равна 120 см², а
- 13. Площадь прямоугольного треугольника равна 168 см². Найдите
- 14. Скачать презентацию
- 15. Похожие презентации








Слайд 4
Свойства площадей многоугольников
Равные многоугольники имеют равные площади.
Если многоугольник
составлен из нескольких многоугольников, то его площадь равна сумме
площадей этих многоугольников.Слайд 8 В прямоугольном треугольнике
квадрат гипотенузы равен сумме квадратов катетов.
c²=a²+b²
Теорема,
обратная теореме Пифагора:если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.
Теорема Пифагора
Слайд 9
8
5
10
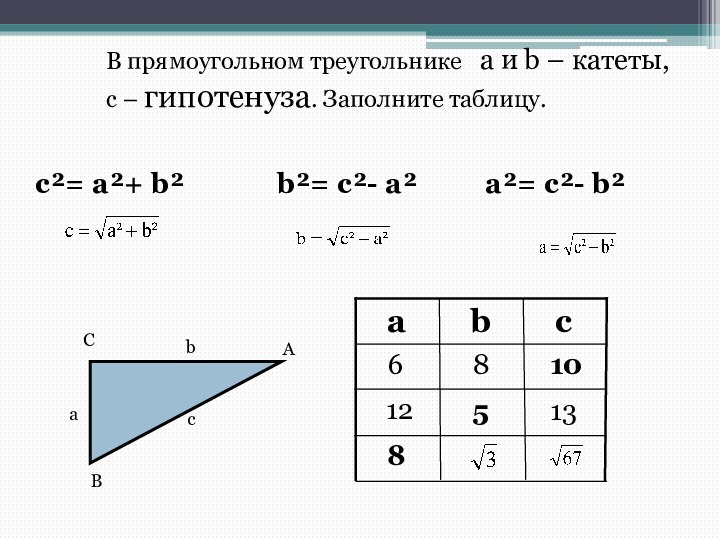
В прямоугольном треугольнике а и b –
катеты,
с – гипотенуза. Заполните таблицу.
c²= a²+ b²
b²= c²-
a²a²= c²- b²
a
B
c
Слайд 10
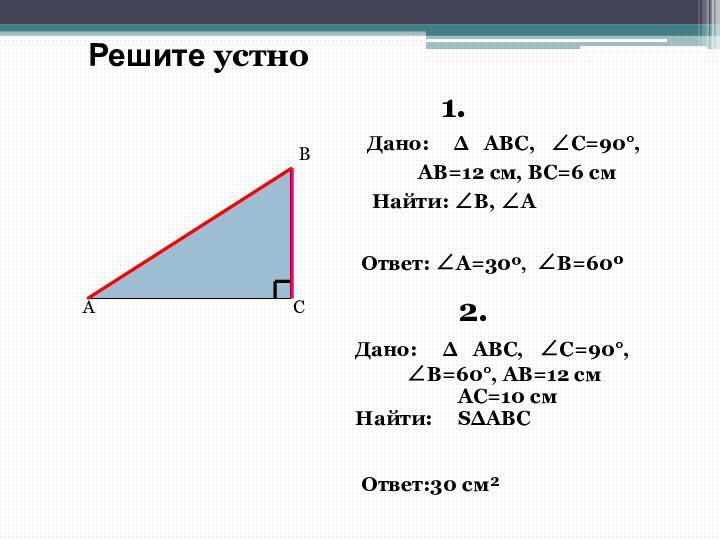
Дано: ∆ ABC, C=90°,
B=60°, AB=12 см
AC=10
см Найти: S∆АВС
Решите устно
C
A
B
Дано: ∆ ABC, C=90°,
AB=12 см, ВC=6 см
Найти: B, А
1.
2.
Ответ: А=30º,
B=60º
Ответ:30 см²
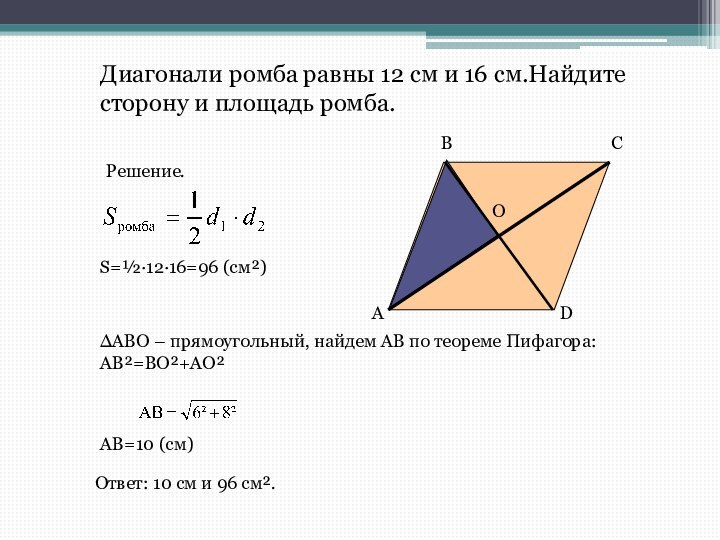
Слайд 11 Диагонали ромба равны 12 см и 16 см.Найдите
сторону и площадь ромба.
Решение.
S=½·12·16=96 (cм²)
∆ABO – прямоугольный, найдем АВ
по теореме Пифагора: АВ²=ВО²+АО²O
АВ=10 (см)
Ответ: 10 см и 96 см².
Слайд 12 Площадь прямоугольной трапеции равна 120 см², а ее
высота 8 см. Найдите все стороны трапеции, если одно
из ее оснований на 6 см больше другого.Н
Дано: ABCD - трапеция,
АВ AD, SАВСD=120 см²,
АВ=8 см, AD>BC на 6 см.
Найти: BС, СD, АD.
Решение.
Пусть ВС=х см, тогда АD=(х+6) см
Т.к. SABCD= 8· (x+6+x)=120,
4(2х+6)=120
2х+6 = 30
х = 12, значит ВС =12 см, АD=18 см
1.
2.
АВ=8 см, ВС=12 см, АD=18 см
Дополнительное построение: СН АD, тогда АВСН – прямоугольник.
СН=АВ=8 см, AH=BC=12 cм, тогда HD=AD-AH=6 cм
12 см
18 см
6 см
Найдем CD по теореме Пифагора: СD²=CH²+HD²
СD=10 (cм)
Ответ: АВ=8 см, ВС=12 см, СD=10 см, AD=18 см.
Слайд 13 Площадь прямоугольного треугольника равна 168 см². Найдите его катеты,
если отношение их длин равно 7:12.
Дано: ∆ABC, С=90º, АC:ВС=7:12,
S∆ABC=168 см² Найти: АС, BС.
Ответ: 14 см и 24 см.
Решение:
S∆ABC=½АС·ВС
168=½ 7 х·12х
168=42х²
х=2
Пусть АС=7х, ВС=12х
АС=14 см, ВС=24 см