- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Решение заданий С5 ЕГЭ
Содержание
- 2.
- 3. Решение.Перепишем систему в видеТогда сможем получить уравнениеили, ПРИМЕР 1.
- 4. Рассмотрим возможные вариантырасположения графиков функцийпри различных значениях параметра ?
- 5. 0 Очевидно, что в этом случае, уравнение, а значит и система уравнений будет иметьединственное решение1
- 6. 0 11. Общих точек нет2. Единственная общая точка - - точка касания3. Две общие точки
- 7.
- 8. Таким образом при наши графики будут иметь
- 9. ПРИМЕР 2.Решение. Рассмотрим возможные варианты.
- 10. Из первого уравнения системы имеем
- 11.
- 12. Решение.ПРИМЕР 3не имеет решений.Рассмотрим второе неравенство системы.
- 13. Определим знаки разностиНанесем найденные числа на числовуюпрямую
- 14. Система неравенств не будет иметь решений в случае, если
- 15. Решим второе неравенство системы.
- 16. ПРИМЕР 4.Решение.Рассмотрим второе уравнение системы.
- 17.
- 18. Решение.Перепишем систему в видеВ результате получаем уравнение, откудаРассмотрим различные варианты расположения графиков функцийПРИМЕР 5.
- 19. 0 В этом случае уравнение будет иметь
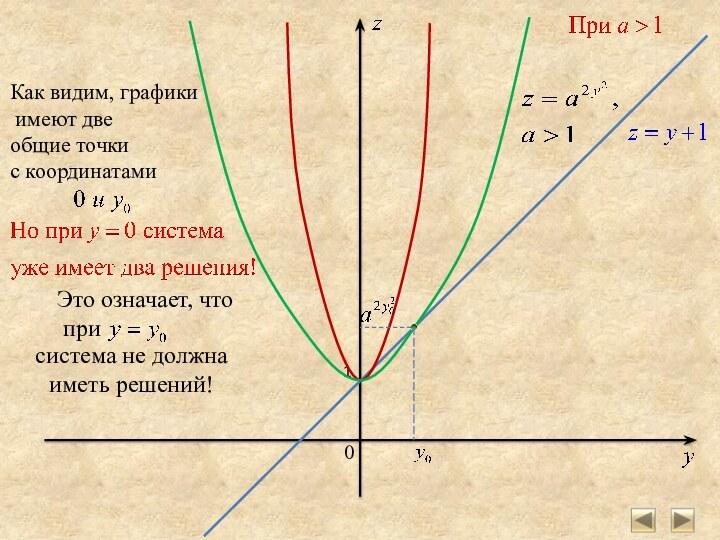
- 20. 0 1Как видим, графики имеют две общие
- 21. Это уравнение является квадратным относительно следовательно оно
- 22. Скачать презентацию
- 23. Похожие презентации





















Слайд 8
Таким образом при
наши графики будут иметь
две
точки пересечения, а значит
система уравнений будет иметь
ровно
два решения.
Слайд 12
Решение.
ПРИМЕР 3
не имеет решений.
Рассмотрим второе неравенство системы.
Выясним,
как располагаются относительно друг друга
найденные значения в
зависимости от параметра.
Слайд 13
Определим знаки разности
Нанесем найденные числа на числовую
прямую и
определим знаки выражения
-1
0
3
Cистема неравенств не будет иметь решений в
случае, если
Слайд 18
Решение.
Перепишем систему в виде
В результате получаем уравнение
, откуда
Рассмотрим
различные варианты расположения графиков функций
ПРИМЕР 5.
Слайд 19
0
В этом случае уравнение
будет иметь
единственный
корень
Подставим это значение
во второе уравнение системы.
Имеем
Таким образом система имеет
ровно два решения
Следовательно при
условие задачи выполнено
1
Слайд 20
0
1
Как видим, графики
имеют две
общие точки
с
координатами
Это означает, что
при система не должна
иметь решений!





























