Презентация на тему Ряд Фурье

и их применение в электротехнике
Примеры решения задач с помощью

рядов Фурье.

Содержание:

и физик, иностранный почетный член Петербургской академии наук. Писал

труды по алгебре, дифференциальным уравнениям и математической физике. Его «Аналитическая теория тепла» явилась основой в создании теории тригонометрических рядов то есть рядов Фурье.

более простых. В общем случае количество таких функций может

быть бесконечным, при этом чем больше таких функций учитывается при расчете, тем выше оказывается конечная точность представления исходной функции. В большинстве случаев в качестве простейших используются тригонометрические функции синуса и косинуса, в этом случае ряд Фурье называется тригонометрическим, а вычисление такого ряда часто называют разложением на гармоники.

называют постоянные числа , aо,an и bn(n=1,2,3…)

 

f(x) .


 сходимость последовательности функций   SN (f,x) к функции  f(x)

 в различных смыслах. Функция f предполагается  2 π - периодической (если она задана только на промежутке , её можно периодически продолжить).Если f є (-  π,  π), то последовательность SN (f,x)  сходится к функции.

ТЕОРЕМА ДИРИХЛЕ
Определение 1. Функция f

(x) называется кусочно-непрерывной на [a;b], если она непрерывна на этом промежутке или имеет на нем конечное число разрывов I рода.
Определение 2. Функция f (x) называется кусочно-непрерывной на [a;b], если она монотонна на всем отрезке, либо этот отрезок можно разбить на конечное число интервалов так, что на каждом из них функция монотонна (т.е. функция на [a;b] имеет конечное число экстремумов).
Определение 3. Говорят, что f (x) удовлетворяет условиям Дирихле на [a;b], если f (x) на [a;b] является кусочно-непрерывной и кусочно- монотонной.

  с периодом 2 π,  , заданную следующим образом:
Данная функция

является кусочно-монотонной и ограниченной, следовательно, она допускает разложение в ряд Фурье. Вычислим коэффициенты Фурье для заданной функции. Поскольку функция равна нулю на промежутке от 0 до π  то для нахождения коэффициентов Фурье интегрирование будем производить только в пределах от – π до 0

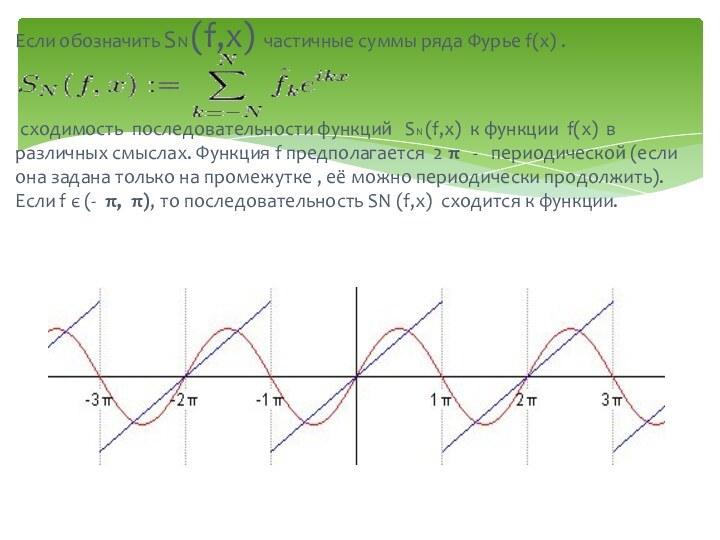
Y=cosx , y=sinx

функции имеет вид

функция    f(x) непрерывна  на отрезке (а,в) или  имеет  на  этом  отрезке 

конечное  число  точек  разрыва  первого  рода.  Рядом  Фурье  такой  функции  f(x) на  отрезке  (а,в) по  ортогональной  системе  

РЯДЫ  ФУРЬЕ  И  ИХ  ПРАКТИЧЕСКОЕ  ПРИМЕНЕНИЕ  В  ЭЛЕКТРОТЕХНИКЕ

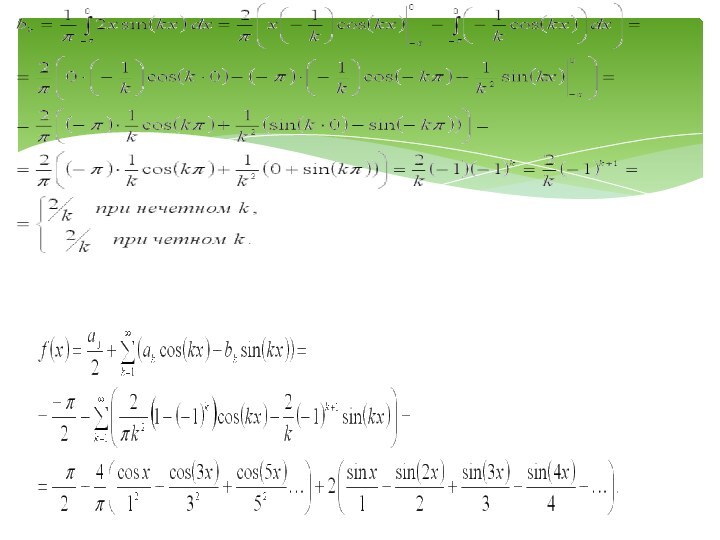
называется  ряд коэффициенты  которого  определяются  равенствами 

и      рассчитываются  по  формулам:
 

Кроме  всего 

этого,  стоит  сказать  о  сумме  тригонометрического  ряда  Фурье.  Все 
функции  системы  являются  периодическими  с  общим  периодом   Поэтому  если  ряд  сходится  на  отрез ке то  он  сходится  и  на  всей  числовой  оси,  а  его  сумма  периодически  повторяет  те 
значения,  которые  она  принимала  на  отрезке. Таким  образом,  можно  говорить  не  только  о  разложении  в  тригонометрический  ряд  Фурье  функции  f(x) на отрезки      .

1.  Электрическая  цепь
Дано:

основной  частоты:
Комплексная  амплитуда  тока  основной  частоты: 

Комплексное  сопротивление  цепи  для 

утроенной  частоты:

вид:

Комплексная амплитуда тока третьей гармоники: